Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T23:43:35.260Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral generating operators for non-stationary processes

Published online by Cambridge University Press:  01 July 2016

D. Tj⊘stheim
D. Tj⊘stheim*
Affiliation:
Royal Norwegian Council for Scientific and Industrial Research (NORSAR)
Get access Rights & Permissions [Opens in a new window]

Abstract

A new method for obtaining spectral-like representations for a large class of non-stationary random processes is formulated. For a wide sense stationary process X(t) in continuous-time the spectral representation is generated by a self-adjoint operator H such that X(t)= eiHt X(0). Extending certain recently established operator identities for wide sense stationary processes, it is shown that similar operators exist for classes of non-stationary processes. 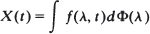The representation generated by such an operator has the form and it shares some of the properties of the wide sense stationary spectral representation: it is dual in a precisely defined sense to the time domain representation of X(t). There exists a class L of linear transformations of X(t) such that for G ∈ L 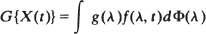for some function g determined by G.

Keywords

NON-STATIONARY PROCESSESSPECTRAL GENERATING OPERATORSCOMMUTATION RELATIONSTIME-FREQUENCY DUALISMINNOVATIONS STABILITYTIME-VARYING SPECTRAL DENSITYSPECTRAL ANALYSERS
Type
Research Article
Information
Advances in Applied Probability , Volume 8 , Issue 4 , December 1976 , pp. 831 - 846
Copyright
Copyright © Applied Probability Trust 1976 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Akhiezer, N. I. and Glazman, I. M. (1963) Theory of Linear Operators in Hilbert Space. Vol. 2. Ungar, New York.Google Scholar
[2] Cramér, H. (1961) On the structure of purely non-deterministic stochastic processes. Ark. Mat. 4, 249–266.CrossRefGoogle Scholar
[3] Cramér, H. (1961) On some classes of non-stationary stochastic processes. Proc. 4th Berkeley Symp. Math. Statist. Prob. 2, 55–77.Google Scholar
[4] Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
[5] Hanner, O. (1950) Deterministic and non-deterministic processes. Ark. Mat. 1, 161–177.CrossRefGoogle Scholar
[6] Kallianpur, G. and Mandrekar, V. (1965) Multiplicity and representation theory of purely non-deterministic stochastic processes. Theor. Prob. Appl. 10, 553–581.Google Scholar
[7] Loynes, R. M. (1968) On the concept of the spectrum for non-stationary processes. J. R. Statist. Soc. B 30, 1–30.Google Scholar
[8] Von Neumann, J. (1931) Die Eindeutigkeit der Schröderingerschen Operatoren. Math. Ann. 104, 570–578.CrossRefGoogle Scholar
[9] Priestley, M. B. (1965) Evolutionary spectra and non-stationary processes. J. R. Statist. Soc. B 27, 204–229.Google Scholar
[10] Priestley, M. B. and Tong, H. (1973) On the analysis of bivariate non-stationary processes. J. R. Statist. Soc. B 35, 153–166.Google Scholar
[11] Putnam, C. R. (1967) Commutation Properties of Hilbert Space Operators and Related Topics. Springer, New York.Google Scholar
[12] Riesz, F. and Nagy, Sz., de, B. (1955) Functional Analysis, 2nd edn. Ungar, New York.Google Scholar
[13] Tj⊘stheim, D. (1976) A commutation relation for wide sense stationary processes. SIAM J. Appl. Math. 30, 115–122.Google Scholar
[14] Tj⊘stheim, D. (1976) Multiplicity theory for multivariate wide sense stationary generalized processes. J. Multivariate Anal. 5, 314–321.CrossRefGoogle Scholar
[15] Whittle, P. (1968) Contribution to the discussion of R. M. Loynes ‘On the concept of the spectrum for a non-stationary process.’ J. R. Statist. Soc. B 30, 26.Google Scholar