Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T08:23:00.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results on the telegraph process driven by gamma components

Part of: Special processes

Published online by Cambridge University Press:  14 June 2022

Barbara Martinucci Open the ORCID record for Barbara Martinucci [Opens in a new window] ,
Alessandra Meoli  and
Shelemyahu Zacks
Barbara Martinucci*
Affiliation:
University of Salerno
Alessandra Meoli*
Affiliation:
University of Salerno
Shelemyahu Zacks*
Affiliation:
Binghamton University
*
*Postal address: Fisciano (SA), I-84084, Italy.
*Postal address: Fisciano (SA), I-84084, Italy.
**Postal address: Binghamton, NY 13902-6000, USA. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the integrated telegraph process 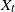$X_t$ under the assumption of general distribution for the random times between consecutive reversals of direction. Specifically, 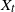$X_t$ represents the position, at time t, of a particle moving U time units upwards with velocity c and D time units downwards with velocity 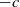$-c$ . The latter motions are repeated cyclically, according to independent alternating renewals. 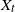Explicit expressions for the probability law of $X_t$ are given in the following cases: (i) (U, D) gamma-distributed; (ii) U exponentially distributed and D gamma-distributed. For certain values of the parameters involved, the probability law of 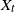$X_t$ is provided in a closed form. Some expressions for the moment generating function of 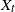$X_t$ and its Laplace transform are also obtained. The latter allows us to prove the existence of a Kac-type condition under which the probability density function of the integrated telegraph process, with identically distributed gamma intertimes, converges to that of the standard Brownian motion.

Finally, we consider the square of 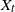$X_t$ and disclose its distribution function, specifying the expression for some choices of the distribution of (U, D).

Keywords

Random motions with finite velocitytelegraph processgamma distributionmoment generating functionKac conditions

MSC classification

Primary: 60K15: Markov renewal processes, semi-Markov processes
Secondary: 60K99: None of the above, but in this section
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 3 , September 2022 , pp. 808 - 848
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (1992). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York.Google Scholar
Asmussen, S. (1995). Stationary distributions for fluid flow models with or without Brownian noise. Stoch. Models 11, 1–20.Google Scholar
Brychkov, Y. A. (2008). Handbook of Special Functions: Derivatives, Integrals, Series and Other Formulas. CRC Press, Boca Raton.CrossRefGoogle Scholar
Brychkov, Y. A. (2017). Reduction formulas for the Appell and Humbert functions. Integral Transforms Spec. Funct. 28, 122–38.Google Scholar
Brychkov, Y. A., Kim, Y. S. and Rathie, A. K. (2017). On new reduction formulas for the Humbert functions $ \Psi_2 $ , $ \Phi_{2} $ and $ \Phi_{3} $ . Integral Transforms Spec. Funct. 28, 350–360.CrossRefGoogle Scholar
Brychkov, Y. A. and Saad, N. (2012). Some formulas for the Appell function $F1\left(a,b,b';c;w,z\right)$ . Integral Transforms Spec. Funct. 23, 793–802.CrossRefGoogle Scholar
Bshouty, D., Di Crescenzo, A., Martinucci, B. and Zacks, S. (2012). Generalized telegraph process with random delays. J. Appl. Prob. 49, 850–865.CrossRefGoogle Scholar
Carlson, B. C. (1966). Some inequalities for hypergeometric functions. Proc. Amer. Math. Soc 17, 32–39.CrossRefGoogle Scholar
Choi, J. and Hasanov, A. (2011). Applications of the operator $ H\left(\alpha,\beta\right) $ to the Humbert double hypergeometric functions. Comput. Math. Appl. 61, 663–671.CrossRefGoogle Scholar
Crimaldi, I., Di Crescenzo, A., Iuliano, A. and Martinucci, B. (2013). A generalized telegraph process with velocity driven by random trials. Adv. Appl. Prob. 45, 1111–1136.CrossRefGoogle Scholar
Davis, M. H. A. (1984). Piecewise-deterministic markov processes: A general class of non-diffusion stochastic models. J. R. Statist. Soc. B 46, 353–388.Google Scholar
Di Crescenzo, A. (2001). On random motions with velocities alternating at Erlang-distributed random times. Adv. Appl. Prob. 33, 690–701.CrossRefGoogle Scholar
Di Crescenzo, A., Iuliano, A., Martinucci, B. and Zacks, S. (2013). Generalized telegraph process with random jumps. J. Appl. Prob. 50, 450–463.CrossRefGoogle Scholar
Di Crescenzo, A. and Martinucci, B. (2007). Random motion with gamma-distributed alternating velocities in biological modeling. In Computer Aided Systems Theory—EUROCAST 2007, eds R. Moreno-Díaz, F. Pichler and A. Quesada-Arencibia, Springer, Berlin, Heidelberg, pp. 163–170.CrossRefGoogle Scholar
Di Crescenzo, A. and Martinucci, B. (2010). A damped telegraph random process with logistic stationary distribution. J. Appl. Prob. 47, 84–96.CrossRefGoogle Scholar
Di Crescenzo, A., Martinucci, B., Paraggio, P. and Zacks, S. (2020). Some results on the telegraph process confined by two non-standard boundaries. Methodology Comput. Appl. Prob. 23, 837–858.CrossRefGoogle Scholar
Di Crescenzo, A. and Pellerey, F. (2002). On prices’ evolutions based on geometric telegrapher’s process. Appl. Stoch. Models Data Anal. 18, 171–184.CrossRefGoogle Scholar
Di Crescenzo, A. and Ratanov, N. (2015). On jump-diffusion processes with regime switching: martingale approach. ALEA 12, 573–596.Google Scholar
Di Crescenzo, A. and Zacks, S. (2015). Probability law and flow function of Brownian motion driven by a generalized telegraph process. Methodology Comput. Appl. Prob. 17, 761–780.CrossRefGoogle Scholar
Fernandez, A., Baleanu, D. and Srivastava, H. M. (2019). Series representations for fractional-calculus operators involving generalized Mittag-Leffler functions. Commun. Nonlinear Sci. Numer. Simul. 67, 517–527.CrossRefGoogle Scholar
Garra, R. and Orsingher, E. (2017). Random motions with space-varying velocities. In Modern Problems of Stochastic Analysis and Statistics, Springer, Cham, pp. 25–39.CrossRefGoogle Scholar
Gnedenko, B. V. and Kovalenko, I. N. (1989). Introduction to Queueing Theory, 2nd edn. Birkhäuser, Boston. (English translation of the Russian edition of 1966.)Google Scholar
Goldstein, S. (1951). On diffusion by discontinuous movements, and on the telegraph equation. Quart. J. Mech. Appl. Math. 4, 129–156.CrossRefGoogle Scholar
Gorenflo, R., Kilbas, A. A., Mainardi, F. and Rogosin, S. V. (2014). Mittag-Leffler Functions, Related Topics and Applications. Springer, Berlin.CrossRefGoogle Scholar
Hansen, E. R. (1975). A Table of Series and Products. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
Humbert, P. (1920). Sur les fonctions hypercylindriques. C. R. Acad. Sci. Paris 171, 490–492.Google Scholar
Jeffrey, A. and Zwillinger, D. (2007). Table of Integrals, Series, and Products, 7th edn. Elsevier, Amsterdam.Google Scholar
Kac, M. (1974). A stochastic model related to the telegrapher’s equation. Rocky Mountain J. Math. 4, 497–509.CrossRefGoogle Scholar
Kilbas, A. A. (2005). Fractional calculus of the generalized Wright function. Fract. Calc. Appl. Anal. 8, 113–126.Google Scholar
Kilbas, A. A., Saigo, M. and Trujillo, J. J. (2002). On the generalized Wright function. Fract. Calc. Appl. Anal. 5, 437–460.Google Scholar
Kolesnik, A. D. (2012). Moment analysis of the telegraph random process. Bul. Acad. Stiinte Repub. Mold. Mat. 1, 90–107.Google Scholar
Kolesnik, A. D. (2018). Linear combinations of the telegraph random processes driven by partial differential equations. Stoch. Dynamics 18, 1850020.CrossRefGoogle Scholar
Kolesnik, A. D. and Ratanov, N. (2013). Telegraph Processes and Option Pricing. Springer, Heidelberg.CrossRefGoogle Scholar
López, O. and Ratanov, N. (2014). On the asymmetric telegraph processes. J. Appl. Prob. 51, 569–589.CrossRefGoogle Scholar
Martinucci, B. and Meoli, A. (2020). Certain functionals of squared telegraph processes. Stoch. Dynamics 20, 2050005.CrossRefGoogle Scholar
Neuman, E. (2013). Inequalities and bounds for the incomplete gamma function. Results Math. 63, 1209–1214.CrossRefGoogle Scholar
Orsingher, E. (1995). Motions with reflecting and absorbing barriers driven by the telegraph equation. Random Operators Stoch. Equat. 3, 9–21.Google Scholar
Perry, D., Stadje, W. and Zacks, S. (1999). Contributions to the theory of first-exit times of some compound processes in queuing theory. Queuing Systems 33, 369–379.CrossRefGoogle Scholar
Perry, D., Stadje, W. and Zacks, S. (1999). First exit times for increasing compound processes. Commun. Statist. Stoch. Models 15, 977–992.CrossRefGoogle Scholar
Pogorui, A. A. and Rodríguez-Dagnino, R. M. (2005). One-dimensional semi-Markov evolutions with general Erlang sojourn times. Random Operators Stoch. Equat. 13, 399–405.CrossRefGoogle Scholar
Pogorui, A. A. and Rodríguez-Dagnino, R. M. (2011). Isotropic random motion at finite speed with K-Erlang distributed direction alternations. J. Statist. Phys. 145, 102–112.CrossRefGoogle Scholar
Pogorui, A. A. and Rodríguez-Dagnino, R. M. (2013). Random motion with gamma steps in higher dimensions. Statist. Prob. Lett. 83, 1638–1643.CrossRefGoogle Scholar
Prudnikov, A. P., Brychkov, Y. A. and Marichev, O. I. (1986). Integrals and Series, Vol. 2, Special Functions. Gordon and Breach, New York.Google Scholar
Prudnikov, A. P., Brychkov, Y. A. and Marichev, O. I. (1990). Integrals and Series, Vol. 3, More Special Functions. Gordon and Breach, New York.Google Scholar
Prudnikov, A. P., Brychkov, Y. A. and Marichev, O. I. (1992). Integrals and Series, Vol. 4, Direct Laplace Transforms. CRC Press, Boca Raton.Google Scholar
Ramaswami, V. (1999). Matrix analytic methods for stochastic fluid flows. In Teletraffic Engineering in a Competitive World (Proc. 16th International Teletraffic Congress, Edinburgh), eds P. Key and D. Smith, Elsevier, Amsterdam, pp. 1019–1030.Google Scholar
Ratanov, N. (2013). Damped jump-telegraph processes. Statist. Prob. Lett. 83, 2282–2290.CrossRefGoogle Scholar
Ratanov, N. (2015). Telegraph processes with random jumps and complete market models. Methodology Comput. Appl. Prob. 17, 677–695.CrossRefGoogle Scholar
Rogers, L. C. (1994). Fluid models in queueing theory and Wiener–Hopf factorization of Markov chains. Ann. Appl. Prob. 4, 390–413.CrossRefGoogle Scholar
Srivastava, H. M. and Tomovski, Z. (2009). Fractional calculus with an integral operator containing a generalized Mittag-Leffler function in the kernel. Appl. Math. Comput. 211, 198–210.Google Scholar
Travaglino, F., Di Crescenzo, A., Martinucci, B. and Scarpa, R. (2018). A new model of Campi Flegrei inflation and deflation episodes based on Brownian motion driven by the telegraph process. Math. Geosci. 50, 961–975.CrossRefGoogle Scholar
Weiss, G. H. (2002). Some applications of persistent random walks and the telegrapher’s equation. Physica A 311, 381–410.CrossRefGoogle Scholar
Zacks, S. (2004). Generalized integrated telegraph processes and the distribution of related stopping times. J. Appl. Prob. 41, 497–507.CrossRefGoogle Scholar
Zacks, S. (2017). Sample Path Analysis and Distributions of Boundary Crossing Times. Springer, Cham.CrossRefGoogle Scholar