Article contents
The sharp threshold for jigsaw percolation in random graphs
Published online by Cambridge University Press: 07 August 2019
Abstract
We analyse the jigsaw percolation process, which may be seen as a measure of whether two graphs on the same vertex set are ‘jointly connected’. Bollobás, Riordan, Slivken, and Smith (2017) proved that, when the two graphs are independent binomial random graphs, whether the jigsaw process percolates undergoes a phase transition when the product of the two probabilities is 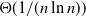 $\Theta({1}/{(n\ln n)})$. We show that this threshold is sharp, and that it lies at
$\Theta({1}/{(n\ln n)})$. We show that this threshold is sharp, and that it lies at 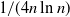 ${1}/{(4n\ln n)}$.
${1}/{(4n\ln n)}$.
MSC classification
Primary:
05C80: Random graphs
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2019
References
Andrews, G. E., Askey, R. and Roy, R. (1999). Special Functions (Encyclopedia Math. Appl. 71). Cambridge University Press.Google Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286
, 509–512.CrossRefGoogle ScholarPubMed
Bollobás, B. and Thomason, A. (1985). Random Graphs of Small Order (North-Holland Math. Stud. 118). North-Holland, Amsterdam, pp. 47–97.CrossRefGoogle Scholar
Bollobás, B., Cooley, O., Kang, M. and Koch, C. (2017). Jigsaw percolation on random hypergraphs. J. Appl. Prob. 54
, 1261–1277.CrossRefGoogle Scholar
Bollobás, B., Riordan, O., Slivken, E., and Smith, P. (2017). The threshold for jigsaw percolation on random graphs. Electron. J. Combinatorics 24, 14pp.Google Scholar
Bollobás, B., Riordan, O., Spencer, J. and Tusnády, G. (2001). The degree sequence of a scale-free random graph process. Random Structures Algorithms 18
, 279–290.CrossRefGoogle Scholar
Brummitt, C. D., Chatterjee, S., Dey, P. S., and Sivakoff, D. (2015). Jigsaw percolation: What social networks can collaboratively solve a puzzle? Ann. Appl. Prob. 25
, 2013–2038.CrossRefGoogle Scholar
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. and Havlin, S. (2010). Catastrophic cascade of failures in interdependent networks. Nature 464
, 1025–1028.CrossRefGoogle ScholarPubMed
Cooley, O. and Gutiérrez, A. (2017). Multi-coloured jigsaw percolation on random graphs. Preprint. Available at https://arxiv.org/abs/1712.00992.Google Scholar
Erdös, P. and Rényi, A. (1959). On random graphs. I. Publ. Math. Debrecen 6
, 290–297.Google Scholar
Gravner, J. and Sivakoff, D. (2017). Nucleation scaling in jigsaw percolation. Ann. Appl. Prob. 27
, 395–438.CrossRefGoogle Scholar
Janson, S., uczak, T., and Ruciski, A. (2000). Random Graphs (Wiley-Interscience Series in Discrete Mathematics and Optimization). Wiley-Interscience, New York.CrossRefGoogle Scholar
Krioukov, D., Papadopoulos, F., Kitsak, M., Vahdat, A. and Boguñá, M. (2010). Hyperbolic geometry of complex networks. Phys. Rev. E (3) 82, 18pp.CrossRefGoogle ScholarPubMed
- 1
- Cited by


