Section means, integral transforms, and Boolean models

Extract

For a stationary particle process X with convex particles in ℝ^dd ≧ 2, a mean body M(X) can be defined by 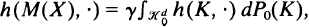where h(M,·) denotes the support function of the convex body M, γ the intensity of X, and P₀ is the distribution of the typical particle of X (a probability measure on the set 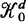of convex bodies with Steiner point at the origin). Replacing the support function h(M,·) by the surface area measure S(M,·) (see Schneider (1993), for the basic notions from convex geometry), we get the Blaschke body B(X) of X, 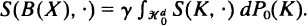After normalization, the left-hand side represents the mean normal distribution of X. The main problem discussed here is whether B(X) (respectively S(B(X), ·)) is uniquely determined by the mean bodies M(X ∩ E) in random planar sections X ∩ E of X. From more general results in Weil (1995), it follows that the expectation ES(M(X ∩ E), ·) (taken w.r.t. the uniform distribution of two-dimensional subspaces E in ℝd) equals the surface area measure of a section mean B₂(B(X)) of B(X). Thus, the formulated stereological question can be reduced to the injectivity of the transform B₂ : K ↦ B₂(K).