Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T08:12:58.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Scan statistics of Lévy noises and marked empirical processes

Part of: Limit theorems Stochastic processes

Published online by Cambridge University Press:  01 July 2016

Zakhar Kabluchko  and
Evgeny Spodarev
Zakhar Kabluchko*
Affiliation:
Georg-August-Universität Göttingen
Evgeny Spodarev*
Affiliation:
Universität Ulm
*
∗ Postal address: Institut für Mathematische Stochastik, Georg-August-Universität Göttingen, Goldschmidtstr. 7, D-37077 Göttingen, Germany. Email address: [email protected]
∗∗ Postal address: Institut für Stochastik, Universität Ulm, Helmholtzstr. 18, D-89069 Ulm, Germany.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let n points be chosen independently and uniformly in the unit cube [0,1]d, and suppose that each point is supplied with a mark, the marks being independent and identically distributed random variables independent of the location of the points. To each cube R contained in [0,1]d we associate its score 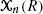defined as the sum of marks of all points contained in R. The scan statistic is defined as the maximum of 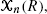taken over all cubes R contained in [0,1]d. We show that if the marks are nonlattice random variables with finite exponential moments, having negative mean and assuming positive values with nonzero probability, then the appropriately normalized distribution of the scan statistic converges as n → ∞ to the Gumbel distribution. We also prove a corresponding result for the scan statistic of a Lévy noise with negative mean. The more elementary cases of zero and positive mean are also considered.

Keywords

Scan statistic with variable window sizemarked empirical processindependently scattered Lévy random measureextremesPickands' double sum method

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60F05: Central limit and other weak theorems
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 41 , Issue 1 , March 2009 , pp. 13 - 37
Copyright
Copyright © Applied Probability Trust 2009 

References

Adler, R. J., Monrad, D., Scissors, R. H. and Wilson, R. (1983). Representations, decompositions and sample function continuity of random fields with independent increments. Stoch. Process. Appl. 15, 3–30.CrossRefGoogle Scholar
Albin, J. M. P. (1990). On extremal theory for stationary processes. Ann. Prob. 18, 92–128.CrossRefGoogle Scholar
Aldous, D. (1989). Probability Approximations via the Poisson Clumping Heuristic (Appl. Math. Sci. 77). Springer, New York.CrossRefGoogle Scholar
Arratia, R., Goldstein, L. and Gordon, L. (1989). Two moments suffice for Poisson approximations: the Chen–Stein method. Ann. Prob. 17, 9–25.CrossRefGoogle Scholar
Bickel, P. J. and Wichura, M. J. (1971). Convergence criteria for multiparameter stochastic processes and some applications. Ann. Math. Statist. 42, 1656–1670.CrossRefGoogle Scholar
Chan, H. P. (2007). Maxima of moving sums in a Poisson random field. Preprint. Available at http://arxiv.org/abs/0708.2764.Google Scholar
Cohen, J. W. (1968). Extreme value distribution for the M/G/1 and the G/M/1 queueing systems. Ann. Inst. H. Poincaré Sect. B 4, 83–98.Google Scholar
Doney, R. A. and Maller, R. A. (2005). Cramér's estimate for a reflected Lévy process. Ann. Appl. Prob. 15, 1445–1450.CrossRefGoogle Scholar
Glaz, J. and Balakrishnan, N. (eds) (1999). Scan Statistics and Applications. Birkhäuser, Boston, MA.CrossRefGoogle Scholar
Glaz, J., Naus, J. and Wallenstein, S. (2001). Scan Statistics. Springer, New York.CrossRefGoogle Scholar
Hüsler, J. and Piterbarg, V. (2004). Limit theorem for maximum of the storage process with fractional Brownian motion as input. Stoch. Process. Appl. 114, 231–250.CrossRefGoogle Scholar
Iglehart, D. L. (1972). Extreme values in the GI/G/1 queue. Ann. Math. Statist. 43, 627–635.CrossRefGoogle Scholar
Jiang, T. (2002). Maxima of partial sums indexed by geometrical structures. Ann. Prob. 30, 1854–1892.CrossRefGoogle Scholar
Karlin, S. and Dembo, A. (1992). Limit distributions of maximal segmental score among Markov-dependent partial sums. Adv. Appl. Prob. 24, 113–140.CrossRefGoogle Scholar
Komlós, J. and Tusnády, G. (1975). On sequences of “pure heads”. Ann. Prob. 3, 608–617.CrossRefGoogle Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H. (1983). Extremes and Related Properties of Random Sequences and Processes. Springer, New York.CrossRefGoogle Scholar
Petrov, V. V. (1965). On the probabilities of large deviations for sums of independent random variables. Teor. Veroyat. Primen. 10, 310–322.Google Scholar
Pickands, J. III (1969). Asymptotic properties of the maximum in a stationary Gaussian process. Trans. Amer. Math. Soc. 145, 75–86.Google Scholar
Pickands, J. III (1969). Upcrossing probabilities for stationary Gaussian processes. Trans. Amer. Math. Soc. 145, 51–73.CrossRefGoogle Scholar
Piterbarg, V. I. (1996). Asymptotic Methods in the Theory of Gaussian Processes and Fields (Trans. Math. Mono. 148). American Mathematical Society, Providence, RI.Google Scholar
Piterbarg, V. I. and Kozlov, A. M. (2003). On large Jumps of a random walk with the Cramér condition. Theory Prob. Appl. 47, 719–729.CrossRefGoogle Scholar
Willekens, E. (1987). On the supremum of an infinitely divisible process. Stoch. Process. Appl. 26, 173–175.CrossRefGoogle Scholar
Zeevi, A. J. and Glynn, P. W. (2000). On the maximum workload of a queue fed by fractional Brownian motion. Ann. Appl. Prob. 10, 1084–1099.Google Scholar