Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jacka, S. D.
and
Roberts, G. O.
1995.
Weak convergence of conditioned processes on a countable state space.
Journal of Applied Probability,
Vol. 32,
Issue. 04,
p.
902.
Jacka, S. D.
and
Roberts, G. O.
1995.
Weak convergence of conditioned processes on a countable state space.
Journal of Applied Probability,
Vol. 32,
Issue. 4,
p.
902.
Martínez, Servet
and
Vares, Maria Eulália
1995.
A Markov chain associated with the minimal quasi-stationary distribution of birth–death chains.
Journal of Applied Probability,
Vol. 32,
Issue. 1,
p.
25.
Ferrari, P. A.
Kesten, H.
and
Martínez, S.
1996.
$R$-positivity, quasi-stationary distributions and ratio limit theorems for a class of probabilistic automata.
The Annals of Applied Probability,
Vol. 6,
Issue. 2,
Boucherie, Richard J.
1997.
On the quasi-stationary distribution for queueing networks with defective routing.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 38,
Issue. 4,
p.
454.
Kijima, Masaaki
and
Makimoto, Naoki
1999.
Applied Probability and Stochastic Processes.
Vol. 19,
Issue. ,
p.
277.
Handelman, David E.
1999.
Eigenvectors and ratio limit theorems for Markov chains and their relatives.
Journal d'Analyse Mathématique,
Vol. 78,
Issue. 1,
p.
61.
Durrett, Rick
1999.
Perplexing Problems in Probability.
p.
1.
Pollett, P.K.
1999.
Modelling quasi-stationary behaviour in metapopulations.
Mathematics and Computers in Simulation,
Vol. 48,
Issue. 4-6,
p.
393.
Bean, N.G.
Pollett, P.K.
and
Taylor, P.G.
2000.
Quasistationary distributions for level-dependent quasi-birth-and-death processes.
Communications in Statistics. Stochastic Models,
Vol. 16,
Issue. 5,
p.
511.
Moler, José A.
Plo, Fernando
and
Miguel, Miguel San
2000.
Minimal quasi-stationary distributions under nullR-recurrence.
Test,
Vol. 9,
Issue. 2,
p.
455.
Coolen-Schrijner, Pauline
Hart, Andrew
and
Pollett, Phil
2000.
Quasistationarity of continuous-time Markov chains with positive drift.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 41,
Issue. 4,
p.
423.
Lasserre, Jean B.
and
Pearce, Charles E. M.
2001.
On the existence of a quasistationary measure for a Markov chain.
The Annals of Probability,
Vol. 29,
Issue. 1,
Koski, Timo
2001.
Hidden Markov Models for Bioinformatics.
Vol. 2,
Issue. ,
p.
245.
Gosselin, Frèdèric
2001.
Aysmptotic Behavior of Absorbing Markov Chains Conditional on Nonabsorption for Applications in Conservation Biology.
The Annals of Applied Probability,
Vol. 11,
Issue. 1,
Coolen-Schrijner, Pauline
and
van Doorn, Erik A.
2006.
Quasi-stationary Distributions for a Class of Discrete-time Markov Chains.
Methodology and Computing in Applied Probability,
Vol. 8,
Issue. 4,
p.
449.
Jacka, Saul
2009.
Markov Chains Conditioned Never to Wait Too Long at the Origin.
Journal of Applied Probability,
Vol. 46,
Issue. 3,
p.
812.
Jacka, Saul
2009.
Markov Chains Conditioned Never to Wait Too Long at the Origin.
Journal of Applied Probability,
Vol. 46,
Issue. 03,
p.
812.
Khanchi, Aziz
2011.
Asymptotic Hitting Distribution for a Reflected Random Walk in the Positive Quadrant.
Stochastic Models,
Vol. 27,
Issue. 2,
p.
169.
Khanchi, Aziz
2012.
Asymptotics of Markov Additive Chains on a Half-Plane: A Ratio Limit Theorem.
Journal of Theoretical Probability,
Vol. 25,
Issue. 1,
p.
62.
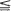 L < ∞ and sequences u1< u2< · ·· and d1d2< · ·· such that Q(i, j) = 0 whenever i < ur < ur + L < j or i > dr + L > dr > j for some r. If Q satisfies some additional uniform irreducibility and aperiodicity assumptions, then for s > 0, Q has at most one positive s-harmonic function and at most one s-invariant measure µ. We use this result to show that if Q is also substochastic, then it has the strong ratio limit property, that is
L < ∞ and sequences u1< u2< · ·· and d1d2< · ·· such that Q(i, j) = 0 whenever i < ur < ur + L < j or i > dr + L > dr > j for some r. If Q satisfies some additional uniform irreducibility and aperiodicity assumptions, then for s > 0, Q has at most one positive s-harmonic function and at most one s-invariant measure µ. We use this result to show that if Q is also substochastic, then it has the strong ratio limit property, that is 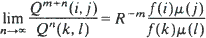
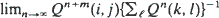 exists. An example shows that this limit may fail to exist if Q does not satisfy the restrictions imposed above, even though Q may have a minimal normalized quasi-stationary distribution (i.e. a probability measure µ for which R–1µ = µQ).
exists. An example shows that this limit may fail to exist if Q does not satisfy the restrictions imposed above, even though Q may have a minimal normalized quasi-stationary distribution (i.e. a probability measure µ for which R–1µ = µQ).

