Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T02:26:00.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Rates of convergence for time series regression

Published online by Cambridge University Press:  01 July 2016

E. J. Hannan
E. J. Hannan*
Affiliation:
The Australian National University, Canberra
Get access Rights & Permissions [Opens in a new window]

Extract

Consider, initially, a time series regression model of the simplest kind, namely 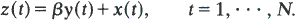Assume that x(t) is second-order stationary with zero mean and absolutely continuous spectrum with density f(ω) so that 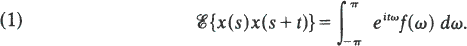The y(t) are taken to be part of a sequence generated entirely independently of x(t) and will be treated as constants. Let 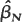βN be the least squares estimate of β and 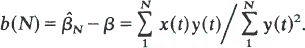Call the numerator and denominator of b(N), respectively, c(N), d(N). We shall use K for a positive finite constant, not always the same one. We have the following result, which is Menchoff's inequality [3].

Type
Research Article
Information
Advances in Applied Probability , Volume 10 , Issue 4 , December 1978 , pp. 740 - 743
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Heyde, C. C. and Scott, D. J. (1973) Invariance principles for the law of iterated logarithm for martingales and processes with stationary increments Ann. Prob. 1, 428–436.CrossRefGoogle Scholar
[2] Neveu, J. (1975) Discrete Parameter Martingales, North Holland, Amsterdam.Google Scholar
[3] Stout, W. F. (1974) Almost Sure Convergence. Academic Press, New York.Google Scholar
[4] Teicher, H. (1974) On the law of the iterated logarithm. Ann. Prob. 2, 714–728.Google Scholar
[5] Feigin, P. D. (1975) Maximum Likelihood for Stochastic Processes—A Martingale Approach. , The Australian National University.Google Scholar
[6] Anderson, T. W. and Taylor, J. B. (1976) Conditions for strong consistency of least squares estimates in linear models. Technical Report No. 213, Institute for Mathematical Studies in the Social Sciences, Stanford University.Google Scholar