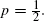Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2006.
The Mathematica GuideBook for Symbolics.
p.
1.
Li, Deli
and
Qi, Yongcheng
2007.
Hierarchical structures associated with order functions.
Statistics & Probability Letters,
Vol. 77,
Issue. 5,
p.
525.
Lacoin, Hubert
and
Moreno, Gregorio
2010.
Directed polymers on hierarchical lattices with site disorder.
Stochastic Processes and their Applications,
Vol. 120,
Issue. 4,
p.
467.
Hambly, B. M.
and
Kumagai, T.
2010.
Diffusion on the Scaling Limit of the Critical Percolation Cluster in the Diamond Hierarchical Lattice.
Communications in Mathematical Physics,
Vol. 295,
Issue. 1,
p.
29.
Benjamini, Itai
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
35.
Mahmoud, Hosam M.
2013.
SOME NODE DEGREE PROPERTIES OF SERIES–PARALLEL GRAPHS EVOLVING UNDER A STOCHASTIC GROWTH MODEL.
Probability in the Engineering and Informational Sciences,
Vol. 27,
Issue. 3,
p.
297.
Alberts, Tom
and
Clark, Jeremy
2019.
Nested Critical Points for a Directed Polymer on a Disordered Diamond Lattice.
Journal of Theoretical Probability,
Vol. 32,
Issue. 1,
p.
64.
Clark, Jeremy Thane
2019.
High-Temperature Scaling Limit for Directed Polymers on a Hierarchical Lattice with Bond Disorder.
Journal of Statistical Physics,
Vol. 174,
Issue. 6,
p.
1372.
Mahmoud, Hosam M.
2019.
A SPECTRUM OF SERIES–PARALLEL GRAPHS WITH MULTIPLE EDGE EVOLUTION.
Probability in the Engineering and Informational Sciences,
Vol. 33,
Issue. 4,
p.
487.
Addario-Berry, L.
Cairns, H.
Devroye, L.
Kerriou, C.
and
Mitchell, R.
2020.
Hipster random walks.
Probability Theory and Related Fields,
Vol. 178,
Issue. 1-2,
p.
437.
Clark, Jeremy Thane
2020.
Continuum directed random polymers on disordered hierarchical diamond lattices.
Stochastic Processes and their Applications,
Vol. 130,
Issue. 3,
p.
1643.
Bhutani, Kiran
Kalpathy, Ravi
and
Mahmoud, Hosam
2021.
Average measures in polymer graphs.
International Journal of Computer Mathematics: Computer Systems Theory,
Vol. 6,
Issue. 1,
p.
37.
Clark, Jeremy Thane
2021.
Weak-Disorder Limit at Criticality for Directed Polymers on Hierarchical Graphs.
Communications in Mathematical Physics,
Vol. 386,
Issue. 2,
p.
651.
Mahmoud, Hosam
2022.
Profile of Random Exponential Recursive Trees.
Methodology and Computing in Applied Probability,
Vol. 24,
Issue. 1,
p.
259.
Kious, Daniel
Mailler, Cécile
and
Schapira, Bruno
2022.
Finding geodesics on graphs using reinforcement learning.
The Annals of Applied Probability,
Vol. 32,
Issue. 5,
Kious, Daniel
Mailler, Cécile
and
Schapira, Bruno
2022.
The trace-reinforced ants process does not find shortest paths.
Journal de l’École polytechnique — Mathématiques,
Vol. 9,
Issue. ,
p.
505.
Addario-Berry, Louigi
Beckman, Erin
and
Lin, Jessica
2024.
Symmetric cooperative motion in one dimension.
Probability Theory and Related Fields,
Vol. 188,
Issue. 1-2,
p.
625.