Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T21:08:48.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Prediction of level crossings for normal processes containing deterministic components

Published online by Cambridge University Press:  01 July 2016

Georg Lindgren
Georg Lindgren*
Affiliation:
University of Umeå
*
∗Postal address: Department of Statistics, University of Umeå, S–90187 Umeå, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

A level crossing predictor is a predictor process Y(t) which can be used to predict whether a specific process X(t) will cross a predetermined level or not. A natural criterion of how good a predictor is can be the probability that a crossing is detected a sufficient time ahead, and the number of times the predictor makes a false alarm.

Suppose the process X(t) consists of a deterministic part A(t) which can be calculated with sufficient accuracy, and a stochastic part Xe(t) which can be predicted by some statistically based predictor 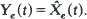An example of this is the prediction of water level near a coast, when A(t) is a sum of known tide components.

The paper develops a tool to handle the detection properties of such predictor processes when used to predict level crossings for the case when A(t) is periodic or is a sum of such functions.

Keywords

PREDICTIONLEVEL CROSSINGSGAUSSIAN PROCESSERGODIC THEORY
Type
Research Article
Information
Advances in Applied Probability , Volume 11 , Issue 1 , March 1979 , pp. 93 - 117
Copyright
Copyright © Applied Probability Trust 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Breiman, L. (1968) Probability. Wiley, New York.Google Scholar
Cramér, H. and Leadbetter, M. R. (1967) Stationary and Related Stochastic Processes. Wiley, New York.Google Scholar
Dahlgaard, P. (1973) Statistical aspects on tide prediction. IMSOR, DTH, Lyngby, Denmark.Google Scholar
Lindgren, G. (1975) Prediction of catastrophes and high level crossings. Bull. Internat. Statist. Inst. 46, (2), 225–240.Google Scholar
Lindgren, G. (1977a) Functional limits of empirical distributions in crossing theory. Stoch. Proc. Appl. 5, 143–149.CrossRefGoogle Scholar
Lindgren, G. (1977b) Marginal and joint ergodicity for bivariate sequences. Statistical Research Report 1977–7, University of Umeå, Sweden.Google Scholar
Marcus, M. B. (1977) Level crossings of a stochastic process with absolutely continuous sample paths. Ann. Prob. 5, 52–71.CrossRefGoogle Scholar
de Maré, J. (1977) Optimal prediction of catastrophes with applications to Gaussian processes. Statistical Research Report 1977–12, University of Umeå, Sweden.Google Scholar
Pinsker, M. S. (1963) Arbeiten zur Informationstheorie, V: Information und Informationsstabilität zufälliger Grössen und Prozesse. VEB Deutscher Verlag der Wissenschaften, Berlin.Google Scholar