Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-30T22:47:08.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Perpetuities with thin tails

Part of: Distribution theory - Probability Stochastic analysis

Published online by Cambridge University Press:  01 July 2016

Charles M. Goldie  and
Rudolf Grübel
Charles M. Goldie
Affiliation:
Queen Mary and Westfield College, University of London
Rudolf Grübel*
Affiliation:
Universität Hannover
*
∗∗ Postal address: Institut für Mathematische Stochastik, Universität Hannover, Postfach 6009, 30060 Hannover, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

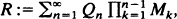We investigate the behaviour of P(R ≧ r) and P(R ≦ −r) as r → ∞for the random variable where 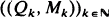is an independent, identically distributed sequence with P(− 1 ≦ M ≦ 1) = 1. Random variables of this type appear in insurance mathematics, as solutions of stochastic difference equations, in the analysis of probabilistic algorithms and elsewhere. Exponential and Poissonian tail behaviour can arise.

Keywords

PERPETUITYRANDOM AFFINE MAPSELECTION ALGORITHMSTOCHASTIC DIFFERENCE EQUATIONSTOCHASTIC DISCOUNTINGTAIL BEHAVIOUR

MSC classification

Primary: 60H25: Random operators and equations 60E99: None of the above, but in this section
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 28 , Issue 2 , June 1996 , pp. 463 - 480
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

∗

Present address: School of Mathematical Sciences, University of Sussex, Brighton, BN1 9QH, UK.

References

Bhattacharya, R. N. and Waymire, E. C. (1990) Stochastic Processes with Applications Wiley-Interscience, New York.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
De Bruijn, N. G. (1951) The asymptotic behaviour of a function occurring in the theory of primes. J. Indian Math. Soc. 15, 25–32.Google Scholar
Embrechts, P. and Goldie, C. M. (1994) Perpetuities and random equations. In Asymptotic Statistics: Proc. Fifth Prague Symp., September 1993. pp. 75–86. ed. Mandl, P. and Hušková, M. Physica, Heidelberg.CrossRefGoogle Scholar
Goldie, C. M. (1991) Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Prob. 1, 126–66.CrossRefGoogle Scholar
Grey, D. R. (1994) Regular variation in the tail behaviour of solutions of random difference equations. Ann. Appl. Prob. 4, 169–183.CrossRefGoogle Scholar
Grincevicius, A. K. (1975) One limit distribution for a random walk on the line. Lithuanian Math. J. 15, 580–589. (Engl. transl. of (1975) Litovsk. Mat. Sb. 15, 79-91.) CrossRefGoogle Scholar
Grübel, R. and Rösler, U. (1996) Asymptotic distribution theory for Hoare's selection algorithm. Adv. Appl. Prob. 28, 252–269.CrossRefGoogle Scholar
Karlsen, H. A. (1990) Existence of moments in a stationary stochastic difference equation. Adv. Appl. Prob. 22, 129–146.CrossRefGoogle Scholar
Kesten, H. (1973) Random difference equations and renewal theory for products of random matrices. Acta Math. 131, 207–248.CrossRefGoogle Scholar
Ohkubo, H. (1979) On the asymptotic tail behaviors of infinitely divisible distributions. Yokohama Math. J. 27, 77–89.Google Scholar
Pötzelberger, K. (1990) A characterisation of random-coefficient AR(1) models. Stoch. Proc. Appl. 34, 171–180.Google Scholar
Sato, K. (1973) A note on infinitely divisible distributions and their Lévy measures. Sci. Rep. Tokyo Kyoiku Daigaku A 12, 101–109.Google Scholar
Vervaat, W. (1977) Success Epochs in Bernoulli Trials (with Applications to Number Theory) 2nd edn. Mathematisch Centrum, Amsterdam.Google Scholar
Vervaat, W. (1979) On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.Google Scholar