Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-27T11:24:17.687Z Has data issue: false hasContentIssue false
  • English
  • Français

PDE for the joint law of the pair of a continuous diffusion and its running maximum

Part of: Stochastic processes Stochastic analysis Markov processes

Published online by Cambridge University Press:  10 July 2023

Laure Coutin  and
Monique Pontier Open the ORCID record for Monique Pontier [Opens in a new window]
Laure Coutin*
Affiliation:
Institut de Mathématiques de Toulouse
Monique Pontier*
Affiliation:
Institut de Mathématiques de Toulouse
*
*Postal address: Institut de Mathématiques de Toulouse, Université Paul Sabatier, 31062 Toulouse CEDEX, France.
*Postal address: Institut de Mathématiques de Toulouse, Université Paul Sabatier, 31062 Toulouse CEDEX, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a d-dimensional diffusion and M the running supremum of its first component. In this paper, we show that for any 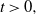$t>0,$ the density (with respect to the 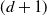$(d+1)$-dimensional Lebesgue measure) of the pair 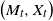$\big(M_t,X_t\big)$ is a weak solution of a Fokker–Planck partial differential equation on the closed set 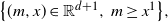$\big\{(m,x)\in \mathbb{R}^{d+1},\,{m\geq x^1}\big\},$ using an integral expansion of this density.

Keywords

Diffusion processpartial differential equationrunning supremum processjoint law

MSC classification

Primary: 60J60: Diffusion processes
Secondary: 60G70: Extreme value theory; extremal processes 60H10: Stochastic ordinary differential equations
Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 4 , December 2023 , pp. 1171 - 1210
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alili, L., Patie, P. and Pedersen, J. L. (2005). Representations of the first hitting time density of an Ornstein–Uhlenbeck process. Stoch. Models 21, 967–980.Google Scholar
Azaïs, J. M. and Wschebor, M. (2001). On the regularity of the distribution of the maximum of one-parameter Gaussian processes. Prob. Theory Relat. Fields 119, 70–98.Google Scholar
Bain, A. and Crisan, D. (2007). Fundamentals of Stochastic Filtering. Springer, New York.Google Scholar
Blanchet-Scalliet, C., Dorobantu, D. and Gay, L. (2020). Joint law of an Ornstein–Uhlenbeck process and its supremum. J. Appl. Prob. 57, 541–558.Google Scholar
Brezis, H. (2011). Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer, New York.Google Scholar
Brown, H., Hobson, D. and Rogers, L. C. G. (2001). Robust hedging of barrier options. Math. Finance 11, 285–314.Google Scholar
Coutin, L. and Dorobantu, D. (2011). First passage time law for some Lévy processes with compound Poisson: existence of a density. Bernoulli 17, 1127–1135.Google Scholar
Coutin, L., Ngom, W. and Pontier, M. (2018). Joint distribution of a Lévy process and its running supremum. J. Appl. Prob. 55, 488–512.Google Scholar
Coutin, L. and Pontier, M. (2019). Existence and regularity of law density of a diffusion and the running maximum of the first component. Statist. Prob. Lett. 153, 130–138.Google Scholar
Cox, A. M. G. and Obloj, J. (2011). Robust hedging of double touch barrier options. SIAM J. Financial Math. 2, 141–182.Google Scholar
Csáki, E., Földes, A. and Salminen, P. (1987). On the joint distribution of the maximum and its location for a linear diffusion. Ann. Inst. H. Poincaré Prob. Statist. 23, 179–194.Google Scholar
Doney, R. A. and Kyprianou, A. E. (2006). Overshoots and undershoots of Lévy processes. Ann. Appl. Prob. 16, 91–106.Google Scholar
Duembgen, M. and Rogers, L. C. G. (2015). The joint law of the extrema, final value and signature of a stopped random walk. In In Memoriam Marc Yor—Séminaire de Probabilités XLVII (Lecture Notes Math. 2137), Springer, Cham, pp. 321–338.Google Scholar
Garroni, M. G. and Menaldi, J.-L. (1992), Green Functions for Second Order Parabolic Integro-Differential Problems. John Wiley, New York.Google Scholar
He, H., Keirstead, W. P. and Rebholz, J. (1998). Double lookbacks. Math. Finance 8, 201–228.Google Scholar
Henry-Labordère, P., Obloj, J., Spoida, P. and Touzi, N. (2016). The maximum maximum of a martingale with given n-marginals. Ann. Appl. Prob. 26, 1–44.Google Scholar
Jeanblanc, M., Yor, M. and Chesney, M. (2009). Mathematical Methods for Financial Markets. Springer, London.Google Scholar
Lamperti, J. (1964). A simple construction of certain diffusion processes. J. Math. Kyoto Univ. 4, 161–170.Google Scholar
Lagnoux, A., Mercier, S. and Vallois, P. (2015). Probability that the maximum of the reflected Brownian motion over a finite interval [0, t] is achieved by its last zero before t. Electron. Commun. Prob. 20, 9 pp.Google Scholar
Ngom, W. (2016). Contributions à l’étude de l’instant de défaut d’un processus de Lévy en observation complète et incomplète. Doctoral Thesis, Institut de Mathématiques de Toulouse.Google Scholar
Nualart, D. (2006). The Malliavin Calculus and Related Topics, 2nd edn. Springer, New York.Google Scholar
Rogers, L. C. G. (1993). The joint law of the maximum and terminal value of a martingale. Prob. Theory Relat. Fields 95, 451–466.Google Scholar
Roynette, B., Vallois, P. and Volpi, A. (2008). Asymptotic behavior of the passage time, overshoot and undershoot for some Lévy processes. ESAIM Prob. Statist. 12, 58–93.Google Scholar