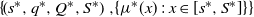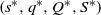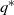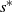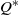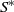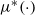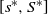1. Introduction
A Brownian system, as one of the simplest stochastic models, is extensively investigated in the optimal control literature. Albeit its simplicity, it has a lot of practical applications. For example, for the inventory and production system, there has been a long history that the inventory-level process is modeled as a Brownian motion since [Reference Bather6]. Also, in the literature of finance and economics, the stock price and the cash flow are typically assumed to follow a diffusion process [Reference Demarzo and Sannikov11, Reference Zhu36]. Besides, in the community that studies queueing models, it is well known that the queue-length process can be approximated by a reflected Brownian motion under heavy traffic conditions in the single-server setting [Reference Chen and Yao9] and that the centered number-in-the-system process can be approximated by a piecewise Ornstein–Uhlenbeck (OU) diffusion process in the many-server setting [Reference Halfin and Whitt15]. Consequently, Brownian control problems (BCPs) frequently arise when studying optimal controls for these systems.
In this paper, we consider a jointly drift rate control and two-sided impulse control problem for a one-dimensional Brownian system, whose state can be negative. Specifically, the drift rate control stipulates the system state’s drift rate at any time instant, which will incur cost continuously over time. The impulse control, on the other side, can adjust the system state instantaneously, with the corresponding cost containing a fixed one that is identical for each adjustment and a variable one that is proportional to the adjustment size. This control is two-sided in the sense that the adjustment can be either upward or downward, with the corresponding cost functions also taking different forms. Our objective is to find a jointly drift rate control and two-sided impulse control to minimize the average expected total costs, including state-related cost, drift-related cost and impulse control cost.
As mentioned in [Reference Cao and Yao7], this type of joint control has several practical scenarios. For example, consider a retailer who maximizes his long-run average profit by dynamically adjusting the production price and controlling the inventory level. Here, dynamic pricing decision can be interpreted as a drift rate control, as it will impact the system state (here, inventory level) via demand process in a smooth manner. Besides, ordering products from or returning products to his supplier can be regarded as two-sided impulse control.
There are few papers studying joint drift rate control and impulse control, and most of them focus on one-sided impulse control in the context of joint pricing and inventory control; see e.g. [Reference Chen, Wu and Yao8, Reference Jack and Zervos20, Reference Yao34, Reference Zhang and Zhang35]. They characterize the optimal policy parameters by assuming the drift rate is constant in certain intervals [Reference Chen, Wu and Yao8, Reference Zhang and Zhang35] or by assuming the existence of the optimal solution [Reference Yao34]. Besides, Sun and Zhu in [Reference Sun and Zhu30] use joint drift rate control and impulse control with finite drift rate choices to study the heavy-traffic approximation of a made-to-order system. There are also several papers considering only drift rate control (see e.g. [Reference Ormeci Matoglu and Vande Vate26–Reference Ormeci Matoglu, Vande Vate and Yu28, Reference Vande Vate31]), only impulse control (see e.g. [Reference Jack and Zervos21]) or joint drift rate control and singular control (see e.g. [Reference Ata, Harrison and Shepp2, Reference Ghosh and Weerasinghe14]), and we refer interested readers to [Reference Cao and Yao7] for a brief survey.
The fundamental distinction between our model and that in [Reference Cao and Yao7] is that their system state is nonnegative while ours can be negative. Although this difference seems insignificant, we shall point out that it is not so because of the following three aspects.
First, from a modelling viewpoint, the system state is imposed to be nonnegative, which makes sense, e.g. in the inventory system, when the unsatisfied demand is lost. However, when the unsatisfied demand is allowed to be backlogged, the inventory level can be negative. The negative-valued system state setting also arises in other systems. As alluded to earlier, in the many-server queueing model, a piecewise OU process is evolved, indicating that the system state can take negative value. To capture this feature, in this paper we relax the nonnegative state constraint in [Reference Cao and Yao7] and consider the drift rate control and two-sided impulse control together in the setting that the system state has range ![]() $\mathbb{R}$.
$\mathbb{R}$.
Second, we use different analysis in solving the free boundary problem described by Equations (6)–(10), which is a crucial step of applying the conventional guess-and-verify method for the BCPs. The importance of this step can also be found in [Reference Gao and Huang13, Reference Sun and Zhu30]. Cao and Yao [Reference Cao and Yao7] tackle this problem by starting from an associated ordinary differential equation (ODE) with an initial boundary condition at zero (a.k.a. the initial value problem), as state 0 is a natural choice, given that the state space is ![]() ${\mathbb{R}_ + }$. However, in the setting studied in this paper, the analysis procedure carried in [Reference Cao and Yao7] fails to work, as there is no apparent starting point when analyzing the associated ODE. To address this issue, in this paper we devise a new procedure by analyzing the ODE with a zero-value condition. Due to the new form of the underlying problem, we need to go through the entire procedure as that in Section 3 of [Reference Cao and Yao7], with an analysis that is different, albeit somewhat similar.
${\mathbb{R}_ + }$. However, in the setting studied in this paper, the analysis procedure carried in [Reference Cao and Yao7] fails to work, as there is no apparent starting point when analyzing the associated ODE. To address this issue, in this paper we devise a new procedure by analyzing the ODE with a zero-value condition. Due to the new form of the underlying problem, we need to go through the entire procedure as that in Section 3 of [Reference Cao and Yao7], with an analysis that is different, albeit somewhat similar.
Finally, our optimal policy has different properties. In this paper, we prove that an ![]() $\{ {( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} ), \{ {{\mu ^{\ast}}(x)\,:\,x \in [ {{s^{\ast}},{S^{\ast}}} ]} \}} \}$ policy is optimal, where the optimal impulse control part takes a control band structure characterized by four parameters
$\{ {( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} ), \{ {{\mu ^{\ast}}(x)\,:\,x \in [ {{s^{\ast}},{S^{\ast}}} ]} \}} \}$ policy is optimal, where the optimal impulse control part takes a control band structure characterized by four parameters ![]() $\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ and where
$\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ and where ![]() ${\mu ^{\ast}}(x)$ specifies the optimal drift rate under state
${\mu ^{\ast}}(x)$ specifies the optimal drift rate under state ![]() $x$. In particular, the state in our model evoking an upward adjustment under the optimal policy must be negative (i.e.
$x$. In particular, the state in our model evoking an upward adjustment under the optimal policy must be negative (i.e. ![]() ${s^{\ast}} \lt 0$), whereas the upward adjustment is made at state 0 in [Reference Cao and Yao7]. Furthermore, our optimal drift rate function
${s^{\ast}} \lt 0$), whereas the upward adjustment is made at state 0 in [Reference Cao and Yao7]. Furthermore, our optimal drift rate function ![]() ${\mu ^{\ast}}\!\left( \cdot \right)$ is firstly increasing, then decreasing and again increasing in
${\mu ^{\ast}}\!\left( \cdot \right)$ is firstly increasing, then decreasing and again increasing in ![]() $[ {{s^{\ast}},{S^{\ast}}}]$, whereas theirs is firstly increasing and then decreasing in a feasible region.
$[ {{s^{\ast}},{S^{\ast}}}]$, whereas theirs is firstly increasing and then decreasing in a feasible region.
Our work is also closely related to the work of Jack and Zervos [Reference Jack and Zervos20]. Although they also consider a joint drift rate and two-sided impulse control problem with the state space being ![]() $\mathbb{R}$, our work differs from theirs, especially in the setting. In fact, they do not consider drift control cost in their control objective and instead specify that the drift rate belongs to an interval determined by the system state. As in their setting the drift control cost rate to be zero, the optimal drift rate always takes one of its boundary values, which significantly simplifies the associated ODE for the value function. Therefore, an explicit solution to the ODE can be obtained (see (3.14)–(3.17) therein), which makes the analysis of determining the optimal impulse control parameters relatively easy. For comparison, no explicit solution to the ODE for our model is available due to the general form of function
$\mathbb{R}$, our work differs from theirs, especially in the setting. In fact, they do not consider drift control cost in their control objective and instead specify that the drift rate belongs to an interval determined by the system state. As in their setting the drift control cost rate to be zero, the optimal drift rate always takes one of its boundary values, which significantly simplifies the associated ODE for the value function. Therefore, an explicit solution to the ODE can be obtained (see (3.14)–(3.17) therein), which makes the analysis of determining the optimal impulse control parameters relatively easy. For comparison, no explicit solution to the ODE for our model is available due to the general form of function ![]() $\pi \!\left( w \right)$, as defined in (5) below, which introduces a significant challenge to our analysis.
$\pi \!\left( w \right)$, as defined in (5) below, which introduces a significant challenge to our analysis.
It is worth mentioning that this paper also presents efficient algorithms (provided in Appendix B) to find the optimal policy parameters and the optimal long-run average cost. With these algorithms in aid, we are able to investigate how the cost parameters impact the optimal policy parameters and quantify the value of drift rate control (see Section 5).
1.1. Organization
The remainder of this paper is organized as follows: The model formulation, the proposed control strategy, as well as the main result of this paper, Theorem 1, which characterizes the best policy parameters, are presented in Section 2. Section 3 contains the proof of Theorem 1, providing a general road map for analyzing similar problems. Section 4 establishes that the proposed policy is indeed optimal among all admissible policies. Section 5 conducts some numerical studies, and Section 6 concludes by providing several directions for future research.
2. Model
Let ![]() $(\Omega,\mathcal{F}, \mathbb{F},\mathbb{P})$ with
$(\Omega,\mathcal{F}, \mathbb{F},\mathbb{P})$ with ![]() $\mathbb{F}=\{\mathcal{F}_t\,:\, t\ge 0\}$ be a filtered probability space, which supports a standard one-dimensional Brownian motion
$\mathbb{F}=\{\mathcal{F}_t\,:\, t\ge 0\}$ be a filtered probability space, which supports a standard one-dimensional Brownian motion ![]() $B = \left\{ {{B_t}\,:\,t \ge 0} \right\},$ with
$B = \left\{ {{B_t}\,:\,t \ge 0} \right\},$ with ![]() ${B_0} = 0$, adapted to the filtration
${B_0} = 0$, adapted to the filtration ![]() $\mathbb{F}$. Consider a Brownian system whose state evolves according to
$\mathbb{F}$. Consider a Brownian system whose state evolves according to
where ![]() ${x_0} \in \mathbb{R}$ is the initial system state,
${x_0} \in \mathbb{R}$ is the initial system state, ![]() ${\mu _s}$ is the drift rate at time
${\mu _s}$ is the drift rate at time ![]() $s$ and
$s$ and ![]() ${\sigma ^2} \gt 0$ is the variance parameter.
${\sigma ^2} \gt 0$ is the variance parameter.
At any time, the system manager can change the drift rate, as well as relocate the inventory level by any amount desired. Let ![]() $\mu = \left\{ {{\mu _t}\,:\,t \ge 0} \right\}$ denote the drift rate control process, and let
$\mu = \left\{ {{\mu _t}\,:\,t \ge 0} \right\}$ denote the drift rate control process, and let ![]() $Y = \left( {{Y_1},{Y_2}} \right)$ be a pair of two-sided impulse controls, with
$Y = \left( {{Y_1},{Y_2}} \right)$ be a pair of two-sided impulse controls, with ![]() ${Y_i} = \left\{ {\!\left( {\tau _n^i,\xi _n^i} \right) \,:\,n \ge 1} \right\}$,
${Y_i} = \left\{ {\!\left( {\tau _n^i,\xi _n^i} \right) \,:\,n \ge 1} \right\}$, ![]() $i = 1,2$, such that
$i = 1,2$, such that ![]() $\tau _n^1$ (resp.
$\tau _n^1$ (resp. ![]() $\tau _n^2$) represents the
$\tau _n^2$) represents the ![]() $n$th time to increase (resp. decrease) the system state and
$n$th time to increase (resp. decrease) the system state and ![]() $\xi _n^1 \ge 0$ (resp.
$\xi _n^1 \ge 0$ (resp. ![]() $\xi _n^2 \ge 0$) denotes the corresponding increment (resp. decrement). These two controls together form a joint drift rate and impulse control policy
$\xi _n^2 \ge 0$) denotes the corresponding increment (resp. decrement). These two controls together form a joint drift rate and impulse control policy ![]() $\phi = \left( {\mu ,Y} \right)$. Such a policy
$\phi = \left( {\mu ,Y} \right)$. Such a policy ![]() $\phi $ is called admissible if: (i) for any
$\phi $ is called admissible if: (i) for any ![]() $t \ge 0$,
$t \ge 0$, ![]() ${\mu _t}$ is
${\mu _t}$ is ![]() ${\mathcal{F}_t}$-measurable and
${\mathcal{F}_t}$-measurable and ![]() ${\mu _t}$ lies in a compact set
${\mu _t}$ lies in a compact set ![]() $\mathcal{U}\subset \mathbb{R}$ with the smallest element
$\mathcal{U}\subset \mathbb{R}$ with the smallest element ![]() $\underline{\mu}$ and the largest element
$\underline{\mu}$ and the largest element ![]() $\bar \mu $; and (ii) for any
$\bar \mu $; and (ii) for any ![]() $i = 1,2$ and
$i = 1,2$ and ![]() $n \ge 1$,
$n \ge 1$, ![]() $\tau _n^i$ is a stopping time and
$\tau _n^i$ is a stopping time and ![]() $\xi _n^i$ is
$\xi _n^i$ is ![]() ${\mathcal{F}_{\tau _n^i - }}$-measurable. We mention that
${\mathcal{F}_{\tau _n^i - }}$-measurable. We mention that ![]() $\mathcal{U}$ might be a discrete point set or a closed interval, and both
$\mathcal{U}$ might be a discrete point set or a closed interval, and both ![]() $\underline{\mu}$ and
$\underline{\mu}$ and ![]() $\bar \mu $ are finite. Let
$\bar \mu $ are finite. Let ![]() ${\rm{\Phi }}$ denote the set of all admissible policies. Under an admissible policy
${\rm{\Phi }}$ denote the set of all admissible policies. Under an admissible policy ![]() $\phi $, the controlled state process
$\phi $, the controlled state process ![]() $X$ is given by
$X$ is given by
 \begin{align}{X_t} = {x_0} + \mathop \int \nolimits_0^t {\mu _s}{\rm{d}}s + \sigma {B_t} + \mathop \sum \limits_{n = 1}^{N_t^1} \xi _n^1 - \mathop \sum \limits_{n = 1}^{N_t^2} \xi _n^2, t \ge 0,\end{align}
\begin{align}{X_t} = {x_0} + \mathop \int \nolimits_0^t {\mu _s}{\rm{d}}s + \sigma {B_t} + \mathop \sum \limits_{n = 1}^{N_t^1} \xi _n^1 - \mathop \sum \limits_{n = 1}^{N_t^2} \xi _n^2, t \ge 0,\end{align}
where ![]() $N_t^i=\sup\{n\in\mathbb{N} \mid \tau^i_n\leq t\}$ denotes the number of adjustments of
$N_t^i=\sup\{n\in\mathbb{N} \mid \tau^i_n\leq t\}$ denotes the number of adjustments of ![]() ${Y_i}$ up to time
${Y_i}$ up to time ![]() $t$ for
$t$ for ![]() $i = 1,2$.
$i = 1,2$.
There are three types of costs to be considered in the model. The first one is the state-related cost, which depends on the current system state and is continuously charged over time. Let the state-related cost rate be ![]() $h(x)$ when the state is
$h(x)$ when the state is ![]() $x$. We take the following assumption about the cost function
$x$. We take the following assumption about the cost function ![]() $h$, which holds throughout the paper.
$h$, which holds throughout the paper.
(i) The function
 $h(x)$ is continuous in
$h(x)$ is continuous in  $x$ on
$x$ on  $\mathbb{R}$, is strictly decreasing in
$\mathbb{R}$, is strictly decreasing in  $x$ on
$x$ on  $\mathbb{R}_-$ and is strictly increasing in
$\mathbb{R}_-$ and is strictly increasing in  $x$ on
$x$ on  $\mathbb{R}_+$ with a unique minimizer 0 such that
$\mathbb{R}_+$ with a unique minimizer 0 such that  $h(0) = 0$.
$h(0) = 0$.-
(ii)
 ${\rm{li}}{{\rm{m}}_{\left| x \right| \to \infty }}h(x) = \infty $.
${\rm{li}}{{\rm{m}}_{\left| x \right| \to \infty }}h(x) = \infty $.
The second type of costs is the drift rate control cost, which is also continuously incurred and depends on the current drift rate. Let this cost rate be ![]() $c\!\left( \mu \right)$ when the drift rate is
$c\!\left( \mu \right)$ when the drift rate is ![]() $\mu $. In this paper,
$\mu $. In this paper, ![]() $c\!\left( \mu \right)$ is assumed to be continuous in
$c\!\left( \mu \right)$ is assumed to be continuous in ![]() $\mu $. (In fact, as in Assumption 1
$\mu $. (In fact, as in Assumption 1![]() $\left( b \right)$ of [Reference Cao and Yao7], we require only that
$\left( b \right)$ of [Reference Cao and Yao7], we require only that ![]() $c\!\left( \mu \right)$ is lower semicontinuous in
$c\!\left( \mu \right)$ is lower semicontinuous in ![]() $\mu $.)
$\mu $.)
The last type of costs that we are considering is the impulse control cost, which incurs when the system state is relocated, either upwardly or downwardly. We distinguish the relocated direction by assuming that a cost ![]() $K + k\xi $ is incurred when the system state is increased by an amount
$K + k\xi $ is incurred when the system state is increased by an amount ![]() $\xi \ge 0$ and that a cost
$\xi \ge 0$ and that a cost ![]() $L + \ell \xi $ is incurred when the system state is decreased by an amount
$L + \ell \xi $ is incurred when the system state is decreased by an amount ![]() $\xi \ge 0$, where
$\xi \ge 0$, where ![]() $K$,
$K$, ![]() $k$,
$k$, ![]() $L$, and
$L$, and ![]() $\ell $ are all positive numbers.
$\ell $ are all positive numbers.
Therefore, under an admissible policy ![]() $\phi $, the system’s long-run average cost is given by
$\phi $, the system’s long-run average cost is given by
 \begin{align}\texttt{AC}\!\left( {{x_0},\phi } \right) = \mathop {{\rm{limsup}}}\limits_{t \to \infty } \frac{1}{t}{{\mathbb E}_{{x_0},\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {h\!\left( {{X_s}} \right) + c\!\left( {{\mu _s}} \right)} \right){\rm{d}}s + \mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right) + \mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right],\end{align}
\begin{align}\texttt{AC}\!\left( {{x_0},\phi } \right) = \mathop {{\rm{limsup}}}\limits_{t \to \infty } \frac{1}{t}{{\mathbb E}_{{x_0},\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {h\!\left( {{X_s}} \right) + c\!\left( {{\mu _s}} \right)} \right){\rm{d}}s + \mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right) + \mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right],\end{align}
where ![]() $X_{0-}=x_0\in\mathbb{R}$ is the initial system state and we write
$X_{0-}=x_0\in\mathbb{R}$ is the initial system state and we write ![]() $\mathbb{E}_{x_0, \phi}$ to demonstrate that the expectation is taken with respect to the initial system state
$\mathbb{E}_{x_0, \phi}$ to demonstrate that the expectation is taken with respect to the initial system state ![]() ${x_0}$ and under control policy
${x_0}$ and under control policy ![]() $\phi $. Here, we write
$\phi $. Here, we write ![]() ${X_{0 - }}$ to indicate that there might be a state relocation at time point 0.
${X_{0 - }}$ to indicate that there might be a state relocation at time point 0.
The system manager’s objective is to find an admissible policy ![]() ${\phi ^{\ast}}$ such that for any
${\phi ^{\ast}}$ such that for any ![]() ${x_0} \in \mathbb{R}$,
${x_0} \in \mathbb{R}$,
2.1. Two-sided Control Band Policies
Motivated by [Reference Cao and Yao7, Reference Ormeci, Dai and Vande Vate25], we consider one particular family of control policies, named two-sided control band policies, which is prescribed by a quadruple ![]() $\left( {s,q,Q,S} \right)$ and a
$\left( {s,q,Q,S} \right)$ and a ![]() $\mathcal{U}$-valued function
$\mathcal{U}$-valued function ![]() $\mu \!\left( \cdot \right)$ defined on
$\mu \!\left( \cdot \right)$ defined on ![]() $\left[ {s,S} \right]$. In this paper, we often use
$\left[ {s,S} \right]$. In this paper, we often use ![]() $\left\{ {\left( {s,q,Q,S} \right),\!\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}} \right\}$ to represent such a policy. In this policy,
$\left\{ {\left( {s,q,Q,S} \right),\!\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}} \right\}$ to represent such a policy. In this policy, ![]() $\left( {s,q,Q,S} \right)$, with
$\left( {s,q,Q,S} \right)$, with ![]() $s \lt q \lt Q \lt S$, is the two-sided impulse control part, and
$s \lt q \lt Q \lt S$, is the two-sided impulse control part, and ![]() $\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}$ is the drift rate control part. Below, we give a precise description of this policy.
$\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}$ is the drift rate control part. Below, we give a precise description of this policy.
The two-sided impulse control part ![]() $\left( {s,q,Q,S} \right)$ prescribes that the system state should be increased up to
$\left( {s,q,Q,S} \right)$ prescribes that the system state should be increased up to ![]() $q$ instantaneously once it drops to
$q$ instantaneously once it drops to ![]() $s$ and should be decreased down to
$s$ and should be decreased down to ![]() $Q$ instantaneously once it rises to
$Q$ instantaneously once it rises to ![]() $S$. Since the initial system state
$S$. Since the initial system state ![]() ${x_0}$ may be lower than
${x_0}$ may be lower than ![]() $s$, an upward relocation with amount
$s$, an upward relocation with amount ![]() $q - {x_0}$ may take place at time 0. Hence,
$q - {x_0}$ may take place at time 0. Hence, ![]() ${Y_1}$ can be specified as
${Y_1}$ can be specified as
 \begin{align*}
\tau_n^1=
\begin{cases}
\inf\{t\geq0\,:\, X_{t-}\le s \} & \text{if $n=1$,}\\
\inf\{t>\tau_{n-1}^1\,:\,X_{t-}= s\} & \text{if $n\geq 2$,}
\end{cases}
\quad \text{ and }
\xi_n^1=
\begin{cases}
q-\min\{s, X_{(\tau^1_1)-}\}& \text{if $n=1$,}\\
q-s & \text{if $n\geq2$}.
\end{cases}
\end{align*}
\begin{align*}
\tau_n^1=
\begin{cases}
\inf\{t\geq0\,:\, X_{t-}\le s \} & \text{if $n=1$,}\\
\inf\{t>\tau_{n-1}^1\,:\,X_{t-}= s\} & \text{if $n\geq 2$,}
\end{cases}
\quad \text{ and }
\xi_n^1=
\begin{cases}
q-\min\{s, X_{(\tau^1_1)-}\}& \text{if $n=1$,}\\
q-s & \text{if $n\geq2$}.
\end{cases}
\end{align*}
Similarly, since ![]() ${x_0}$ may be higher than
${x_0}$ may be higher than ![]() $S$, a downward relocation with amount
$S$, a downward relocation with amount ![]() ${x_0} - Q$ may happen at time 0. Therefore,
${x_0} - Q$ may happen at time 0. Therefore, ![]() ${Y_2}$ can be specified as
${Y_2}$ can be specified as
 \begin{align*}
\tau_n^2=
\begin{cases}
\inf\{t\geq0\,:\, X_{t-}\geq S\} & \text{if $n=1$,}\\
\inf\{t>\tau_{n-1}^2\,:\,X_{t-}= S\} & \text{if $n\geq 2,$}
\end{cases}
\text{ and }
\xi_n^2=
\begin{cases}
\max\{S, X_{(\tau^2_1)-}\}-Q& \text{if $n=1$,}\\
S-Q & \text{if $n\geq2$}.
\end{cases}
\end{align*}
\begin{align*}
\tau_n^2=
\begin{cases}
\inf\{t\geq0\,:\, X_{t-}\geq S\} & \text{if $n=1$,}\\
\inf\{t>\tau_{n-1}^2\,:\,X_{t-}= S\} & \text{if $n\geq 2,$}
\end{cases}
\text{ and }
\xi_n^2=
\begin{cases}
\max\{S, X_{(\tau^2_1)-}\}-Q& \text{if $n=1$,}\\
S-Q & \text{if $n\geq2$}.
\end{cases}
\end{align*}
The impulse control policy ![]() $\left( {s,q,Q,S} \right)$ is called a control band policy in the literature [Reference Harrison, Sellke and Taksar17, Reference Ormeci, Dai and Vande Vate25]. Note that under control band policy
$\left( {s,q,Q,S} \right)$ is called a control band policy in the literature [Reference Harrison, Sellke and Taksar17, Reference Ormeci, Dai and Vande Vate25]. Note that under control band policy ![]() $\left( {s,q,Q,S} \right)$, the controlled system state
$\left( {s,q,Q,S} \right)$, the controlled system state ![]() ${X_t}$ is limited to
${X_t}$ is limited to ![]() $\left[ {s,S} \right]$ for all
$\left[ {s,S} \right]$ for all ![]() $t \ge 0$. Consequently, we need to specify only the drift rate control policy when the system state lies in
$t \ge 0$. Consequently, we need to specify only the drift rate control policy when the system state lies in ![]() $\left[ {s,S} \right]$. In fact, the drift rate control part
$\left[ {s,S} \right]$. In fact, the drift rate control part ![]() $\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}$ prescribes that the drift rate be set to
$\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}$ prescribes that the drift rate be set to ![]() $\mu (x)$ if the system state is
$\mu (x)$ if the system state is ![]() $x,$ with
$x,$ with ![]() $x \in \left[ {s,S} \right]$.
$x \in \left[ {s,S} \right]$.
2.2. Finding the Best Policy Parameters
In this section, we will determine the best policy parameters in the family of policies described in Section 2.1. To begin, we define two functions as follows:
where we choose ![]() $\hat \mu \!\left( w \right)$ to be the smallest if there are multiple minimizers.
$\hat \mu \!\left( w \right)$ to be the smallest if there are multiple minimizers.
In Section 3, we show the following result, which also specifies the conditions that the optimal policy parameters should satisfy.
(i) There exist five unique parameters
 ${s^{\ast}}$,
${s^{\ast}}$,  ${q^{\ast}}$,
${q^{\ast}}$,  ${Q^{\ast}}$,
${Q^{\ast}}$,  ${S^{\ast}}$ and
${S^{\ast}}$ and  ${\gamma ^{\ast}},$ with
${\gamma ^{\ast}},$ with  ${s^{\ast}} \lt {q^{\ast}} \lt {Q^{\ast}} \lt {S^{\ast}}$ and
${s^{\ast}} \lt {q^{\ast}} \lt {Q^{\ast}} \lt {S^{\ast}}$ and  ${\gamma ^{\ast}} \in {\mathbb{R}_ + }$, and a continuously differentiable function
${\gamma ^{\ast}} \in {\mathbb{R}_ + }$, and a continuously differentiable function  $w^{\star}({\cdot})\,:\,\mathbb{R}\to\mathbb{R}$ such that the following equations hold:
(6)
$w^{\star}({\cdot})\,:\,\mathbb{R}\to\mathbb{R}$ such that the following equations hold:
(6) \begin{align}\frac{1}{2}{\sigma ^2}{\!\left( {{w^{\ast}}} \right)^{\prime}}(x) + \pi \!\left( {{w^{\ast}}(x)} \right) + h(x) = {\gamma ^{\ast}} for\ x \in \left[ {{{\rm{s}}^{\ast}},{{\rm{S}}^{\ast}}} \right],\end{align}
(7)
\begin{align}\frac{1}{2}{\sigma ^2}{\!\left( {{w^{\ast}}} \right)^{\prime}}(x) + \pi \!\left( {{w^{\ast}}(x)} \right) + h(x) = {\gamma ^{\ast}} for\ x \in \left[ {{{\rm{s}}^{\ast}},{{\rm{S}}^{\ast}}} \right],\end{align}
(7) \begin{align}\mathop \int \nolimits_{{s^{\ast}}}^{{q^{\ast}}} \!\left( {{w^{\ast}}(x) + k} \right){\rm{d}}x = - K,\end{align}
(8)
\begin{align}\mathop \int \nolimits_{{s^{\ast}}}^{{q^{\ast}}} \!\left( {{w^{\ast}}(x) + k} \right){\rm{d}}x = - K,\end{align}
(8) \begin{align}\mathop \int \nolimits_{{Q^{\ast}}}^{{S^{\ast}}} \!\left( {{w^{\ast}}(x) - \ell } \right)\;{\rm{d}}x = L,\end{align}
(9)
\begin{align}\mathop \int \nolimits_{{Q^{\ast}}}^{{S^{\ast}}} \!\left( {{w^{\ast}}(x) - \ell } \right)\;{\rm{d}}x = L,\end{align}
(9) \begin{align}{w^{\ast}}( {{s^{\ast}}}) = {w^{\ast}}\!\left( {{q^{\ast}}} \right) = - k,\end{align}
(10)Moreover,
\begin{align}{w^{\ast}}( {{s^{\ast}}}) = {w^{\ast}}\!\left( {{q^{\ast}}} \right) = - k,\end{align}
(10)Moreover, \begin{align}{w^{\ast}}\!\left( {{Q^{\ast}}} \right) = {w^{\ast}}\!\left( {{S^{\ast}}} \right) = \ell.\end{align}
\begin{align}{w^{\ast}}\!\left( {{Q^{\ast}}} \right) = {w^{\ast}}\!\left( {{S^{\ast}}} \right) = \ell.\end{align}
 ${s^{\ast}} \lt 0 \lt {S^{\ast}}$.
${s^{\ast}} \lt 0 \lt {S^{\ast}}$.
(ii) Define
 ${\mu ^{\ast}}(x) = \hat \mu \!\left( {{w^{\ast}}(x)} \right)$. Then
${\mu ^{\ast}}(x) = \hat \mu \!\left( {{w^{\ast}}(x)} \right)$. Then  ${\phi ^{\ast}} = \left\{ {\!\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right),\!\left\{ {{\mu ^{\ast}}(x)\,:\,x \in [ {{s^{\ast}},{S^{\ast}}}]} \right\}} \right\}$ is an admissible policy. Furthermore, there exist two numbers
${\phi ^{\ast}} = \left\{ {\!\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right),\!\left\{ {{\mu ^{\ast}}(x)\,:\,x \in [ {{s^{\ast}},{S^{\ast}}}]} \right\}} \right\}$ is an admissible policy. Furthermore, there exist two numbers  $x_1^{\ast}$ and
$x_1^{\ast}$ and  $x_2^{\ast}$ with
$x_2^{\ast}$ with  $x_1^{\ast} \in \left( {{Q^{\ast}},{S^{\ast}}} \right)$ and
$x_1^{\ast} \in \left( {{Q^{\ast}},{S^{\ast}}} \right)$ and  $x_2^{\ast} \in ( {{s^{\ast}},{q^{\ast}}})$ such that
$x_2^{\ast} \in ( {{s^{\ast}},{q^{\ast}}})$ such that  ${\mu ^{\ast}}(x)$ is increasing in
${\mu ^{\ast}}(x)$ is increasing in  $x$ on
$x$ on  $\left[ {{s^{\ast}},x_2^{\ast}} \right]$, decreasing on
$\left[ {{s^{\ast}},x_2^{\ast}} \right]$, decreasing on  $\left[ {x_2^{\ast},x_1^{\ast}} \right]$ and increasing on
$\left[ {x_2^{\ast},x_1^{\ast}} \right]$ and increasing on  $\left[ {x_1^{\ast},{S^{\ast}}} \right]$.
$\left[ {x_1^{\ast},{S^{\ast}}} \right]$.
With a similar definition in [Reference Dai and Yao10], we call Equations (7)–(10) free boundary conditions since the boundary points ![]() ${s^{\ast}}$,
${s^{\ast}}$, ![]() ${q^{\ast}}$,
${q^{\ast}}$, ![]() ${Q^{\ast}}$, and
${Q^{\ast}}$, and ![]() ${S^{\ast}}$ need to be determined, and call problem (6) with conditions in Equations (7)–(10) a free boundary problem. Please refer to Appendix A for a heuristic derivation of these conditions. In fact, the policy
${S^{\ast}}$ need to be determined, and call problem (6) with conditions in Equations (7)–(10) a free boundary problem. Please refer to Appendix A for a heuristic derivation of these conditions. In fact, the policy ![]() ${\phi ^{\ast}}$ as defined in Theorem 1, is optimal in the sense that it minimizes the system’s long run average cost. This will be shown in Theorem 2 below.
${\phi ^{\ast}}$ as defined in Theorem 1, is optimal in the sense that it minimizes the system’s long run average cost. This will be shown in Theorem 2 below.
3. Proof of Theorem 1
This section is devoted to the proof of Theorem 1, which contains two parts. First, in Section 3.1, we solve the ODE (O) below for any given ![]() $\gamma\in\mathbb{R}$ with condition
$\gamma\in\mathbb{R}$ with condition ![]() $w(\vartheta) = 0$, and provide several structural properties of its solution with respect to
$w(\vartheta) = 0$, and provide several structural properties of its solution with respect to ![]() $x$,
$x$, ![]() $\vartheta $, and
$\vartheta $, and ![]() $\gamma $. Next, in Section 3.2, we determine
$\gamma $. Next, in Section 3.2, we determine ![]() $\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}},{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ by the six boundary conditions (7)–(10).
$\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}},{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ by the six boundary conditions (7)–(10).
Before proving Theorem 1, recalling the definitions of ![]() $\pi \!\left( w \right)$ and
$\pi \!\left( w \right)$ and ![]() $\hat \mu \!\left( w \right)$ in Equation (5), we first give the following lemma, whose proof is omitted as it is exactly Lemma 4 in [Reference Cao and Yao7].
$\hat \mu \!\left( w \right)$ in Equation (5), we first give the following lemma, whose proof is omitted as it is exactly Lemma 4 in [Reference Cao and Yao7].
Lemma 1. The function ![]() $\pi \!\left( w \right)$ is concave and Lipschitz continuous in
$\pi \!\left( w \right)$ is concave and Lipschitz continuous in ![]() $w$. In particular, for any
$w$. In particular, for any ![]() ${w_1}$ and
${w_1}$ and ![]() ${w_2}$, we have
${w_2}$, we have
where ![]() $M\,:\!=\, {\rm{max}}\big\{ {| {\underline \mu | , |\hat \mu } |} \big\}$. Furthermore,
$M\,:\!=\, {\rm{max}}\big\{ {| {\underline \mu | , |\hat \mu } |} \big\}$. Furthermore, ![]() $\hat \mu \!\left( w \right)$ is decreasing in
$\hat \mu \!\left( w \right)$ is decreasing in ![]() $w$.
$w$.
3.1. Solving the ODE
In this subsection, we will consider the ODE (O) below with condition ![]() $w(\vartheta) = 0$ for any
$w(\vartheta) = 0$ for any ![]() $\vartheta\in\mathbb{R}$ and
$\vartheta\in\mathbb{R}$ and ![]() $\gamma\in\mathbb{R}$ and characterize the structural and asymptotical properties of its solution.
$\gamma\in\mathbb{R}$ and characterize the structural and asymptotical properties of its solution.
Consider the following problem:
 \begin{align}&\frac{1}{2}\sigma^2 w'(x)+\pi(w(x))+h(x)=\gamma \quad\text{for $x\in\mathbb{R}$},
\\
&\qquad \text{subject to } w(\vartheta)=0. \nonumber\end{align}
\begin{align}&\frac{1}{2}\sigma^2 w'(x)+\pi(w(x))+h(x)=\gamma \quad\text{for $x\in\mathbb{R}$},
\\
&\qquad \text{subject to } w(\vartheta)=0. \nonumber\end{align}
To highlight the dependence on ![]() $\vartheta $ and
$\vartheta $ and ![]() $\gamma $, we denote the solution of the above problem by
$\gamma $, we denote the solution of the above problem by ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$, if it exists.
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$, if it exists.
Before presenting properties of the solution to problem (O), it is worth mentioning the difference between problem (O) and the initial value problem (IVP), which has been extensively studied in the approximating diffusion control problem for queueing systems; see e.g. [Reference Ata, Harrison and Shepp2, Reference Ata and Tongarlak5]. In the IVP, the condition takes the form ![]() $w(0) = {w_0}$ for some
$w(0) = {w_0}$ for some ![]() ${w_0} \in \mathbb{R}$, which makes sense, as the corresponding state space is
${w_0} \in \mathbb{R}$, which makes sense, as the corresponding state space is ![]() $\mathbb{R}_+$ due to the nonnegativity of the queue length. In our problem (O), however, to facilitate the analysis of the solution function, as in [Reference Jack and Zervos20], we use a different form of the condition, which is
$\mathbb{R}_+$ due to the nonnegativity of the queue length. In our problem (O), however, to facilitate the analysis of the solution function, as in [Reference Jack and Zervos20], we use a different form of the condition, which is ![]() $w(\vartheta) = 0$.
$w(\vartheta) = 0$.
It is also worth pointing out that there are a few works that study joint drift rate and singular control for Brownian motion with state space ![]() $\mathbb{R}$; see e.g. [Reference Ata, Lee and Sönmez3, Reference Koçağa23]. The associated analysis is conducted by considering two IVPs on
$\mathbb{R}$; see e.g. [Reference Ata, Lee and Sönmez3, Reference Koçağa23]. The associated analysis is conducted by considering two IVPs on ![]() $\mathbb{R}_-$ and
$\mathbb{R}_-$ and ![]() $\mathbb{R}_+$ separately, as the drift rates in their settings take different forms between
$\mathbb{R}_+$ separately, as the drift rates in their settings take different forms between ![]() ${\mathbb{R}_ - }$ and
${\mathbb{R}_ - }$ and ![]() ${\mathbb{R}_ + }$. Then the continuity of the value function at the origin will be used to pin down
${\mathbb{R}_ + }$. Then the continuity of the value function at the origin will be used to pin down ![]() $\gamma $. This analysis procedure seems unapplicable to our setting, as the signs of
$\gamma $. This analysis procedure seems unapplicable to our setting, as the signs of ![]() ${s^{\ast}}$ and
${s^{\ast}}$ and ![]() ${q^{\ast}}$ can be either negative or positive. Besides, thanks to Lemma 1, the solution to (O) will not explode in finite time, which is also different from [Reference Koçağa23].
${q^{\ast}}$ can be either negative or positive. Besides, thanks to Lemma 1, the solution to (O) will not explode in finite time, which is also different from [Reference Koçağa23].
We first have the following lemma, which states the existence, uniqueness and continuity of the solution to (O). Throughout this paper, we will use ![]() $w'( {x;\, \vartheta ,\gamma })$ to denote
$w'( {x;\, \vartheta ,\gamma })$ to denote ![]() $\partial w( {x;\, \vartheta ,\gamma })/\partial x$.
$\partial w( {x;\, \vartheta ,\gamma })/\partial x$.
(i) For any
 $\vartheta \in \mathbb{R}$ and
$\vartheta \in \mathbb{R}$ and  $\gamma \in \mathbb{R}$, problem (O) has a unique continuously differentiable solution, which is denoted as
$\gamma \in \mathbb{R}$, problem (O) has a unique continuously differentiable solution, which is denoted as  $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$.
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$.-
(ii) For any
 $x \in \mathbb{R}$,
$x \in \mathbb{R}$,  $w( {x;\, \vartheta ,\gamma })$ is continuous in
$w( {x;\, \vartheta ,\gamma })$ is continuous in  $( {\vartheta ,\gamma })$, and
$( {\vartheta ,\gamma })$, and  $w'( {x;\, \vartheta ,\gamma })$ is continuous in
$w'( {x;\, \vartheta ,\gamma })$ is continuous in  $\left( {x,\vartheta ,\gamma } \right)$.
$\left( {x,\vartheta ,\gamma } \right)$.
Proof. (![]() $a$) Since
$a$) Since ![]() $\pi \!\left( \cdot \right)$ is Lipschitz continuous (see Lemma 2) and
$\pi \!\left( \cdot \right)$ is Lipschitz continuous (see Lemma 2) and ![]() $h\!\left( \cdot \right)$ is continuous (see Assumption 1), using a similar argument as that in the proof of Proposition 3(i) in [Reference Ata and Tongarlak5], we can employ Picard’s existence theorem (see e.g. Theorem 10 of Section 1.7 in [Reference Adkins and Davidson1]) to show that there exists a unique continuous solution
$h\!\left( \cdot \right)$ is continuous (see Assumption 1), using a similar argument as that in the proof of Proposition 3(i) in [Reference Ata and Tongarlak5], we can employ Picard’s existence theorem (see e.g. Theorem 10 of Section 1.7 in [Reference Adkins and Davidson1]) to show that there exists a unique continuous solution ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ to (O) on
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ to (O) on ![]() $\mathbb{R}$.
$\mathbb{R}$.
(![]() $b$) It follows from Theorem II-1-2 in [Reference Hsieh and Sibuya19], part (2) of this lemma as well as the continuity of
$b$) It follows from Theorem II-1-2 in [Reference Hsieh and Sibuya19], part (2) of this lemma as well as the continuity of ![]() $h\!\left( \cdot \right)$ that
$h\!\left( \cdot \right)$ that ![]() $w( {x;\, \vartheta ,\gamma })$ is continuous in
$w( {x;\, \vartheta ,\gamma })$ is continuous in ![]() $\vartheta $ and
$\vartheta $ and ![]() $\gamma $. Further, (O) and the continuity of
$\gamma $. Further, (O) and the continuity of ![]() $h\!\left( \cdot \right)$,
$h\!\left( \cdot \right)$, ![]() $\pi \!\left( \cdot \right)$ and
$\pi \!\left( \cdot \right)$ and ![]() $w\!\left( \cdot \right)$ immediately imply the continuity of
$w\!\left( \cdot \right)$ immediately imply the continuity of ![]() $w'( {x;\, \vartheta ,\gamma })$ in
$w'( {x;\, \vartheta ,\gamma })$ in ![]() $x$,
$x$, ![]() $\vartheta $, and
$\vartheta $, and ![]() $\gamma $.
$\gamma $.
It follows from (11) (by letting ![]() ${w_1} = w( {x;\, \vartheta ,\gamma })$ and
${w_1} = w( {x;\, \vartheta ,\gamma })$ and ![]() ${w_2} = 0$) and (O) that
${w_2} = 0$) and (O) that
These two inequalities will be used in the subsequent analysis.
The following lemma characterizes the monotonicity and asymptotical behaviors of ![]() $w( {x;\, \vartheta ,\gamma }),$ with respect to
$w( {x;\, \vartheta ,\gamma }),$ with respect to ![]() $\gamma $ for any given
$\gamma $ for any given ![]() $\vartheta $.
$\vartheta $.
(i) If
 $x \gt \vartheta $, then
$x \gt \vartheta $, then  $w( {x;\, \vartheta ,\gamma })$ is strictly increasing in
$w( {x;\, \vartheta ,\gamma })$ is strictly increasing in  $\gamma $ with
$\gamma $ with  $li{m_{\gamma \to \pm \infty }}w( {x;\, \vartheta ,\gamma }) = \pm \infty $; and
$li{m_{\gamma \to \pm \infty }}w( {x;\, \vartheta ,\gamma }) = \pm \infty $; and-
(ii) If
 $x \lt \vartheta $, then
$x \lt \vartheta $, then  $w( {x;\, \vartheta ,\gamma })$ is strictly decreasing in
$w( {x;\, \vartheta ,\gamma })$ is strictly decreasing in  $\gamma $ with
$\gamma $ with  $li{m_{\gamma \to \pm \infty }}w( {x;\, \vartheta ,\gamma }) = \mp \infty $.
$li{m_{\gamma \to \pm \infty }}w( {x;\, \vartheta ,\gamma }) = \mp \infty $.
Proof. ![]() $(a)$ For any
$(a)$ For any ![]() $x \gt \vartheta $, we show that
$x \gt \vartheta $, we show that ![]() $w\!\left( {x;\, \vartheta ,{\gamma _1}} \right) \lt w\!\left( {x;\, \vartheta ,{\gamma _2}} \right)$ if
$w\!\left( {x;\, \vartheta ,{\gamma _1}} \right) \lt w\!\left( {x;\, \vartheta ,{\gamma _2}} \right)$ if ![]() ${\gamma _1} \lt {\gamma _2}$. Suppose, to the contradictory, that
${\gamma _1} \lt {\gamma _2}$. Suppose, to the contradictory, that ![]() $w\!\left( {x;\, \vartheta ,{\gamma _1}} \right) \ge w\!\left( {x;\, \vartheta ,{\gamma _2}} \right)$ for some
$w\!\left( {x;\, \vartheta ,{\gamma _1}} \right) \ge w\!\left( {x;\, \vartheta ,{\gamma _2}} \right)$ for some ![]() $x \gt \vartheta $. Define
$x \gt \vartheta $. Define
It follows from (O) that
Taking ![]() $x = \vartheta $ in (14), we obtain that
$x = \vartheta $ in (14), we obtain that ![]() $f'_{\!\!\gamma }(\vartheta) = 2\!\left( {{\gamma _2} - {\gamma _1}} \right)/{\sigma ^2} \gt 0$. Moreover,
$f'_{\!\!\gamma }(\vartheta) = 2\!\left( {{\gamma _2} - {\gamma _1}} \right)/{\sigma ^2} \gt 0$. Moreover, ![]() ${f_\gamma }(\vartheta) = 0$. Hence, we must have
${f_\gamma }(\vartheta) = 0$. Hence, we must have ![]() ${x_\gamma } \gt \vartheta $. Then, by the continuity of
${x_\gamma } \gt \vartheta $. Then, by the continuity of ![]() $w\!\left( { \cdot ;\,\vartheta ,{\gamma _i}} \right)$, we obtain that
$w\!\left( { \cdot ;\,\vartheta ,{\gamma _i}} \right)$, we obtain that ![]() ${f_\gamma }\!\left( {{x_\gamma }} \right) = 0 = {f_\gamma }(\vartheta)$ and
${f_\gamma }\!\left( {{x_\gamma }} \right) = 0 = {f_\gamma }(\vartheta)$ and ![]() ${f_\gamma }(x) \gt 0$ for all
${f_\gamma }(x) \gt 0$ for all ![]() $x \in \left( {\vartheta ,{x_\gamma }} \right)$. By the continuity of
$x \in \left( {\vartheta ,{x_\gamma }} \right)$. By the continuity of ![]() ${f_\gamma }\!\left( \cdot \right)$, there exists a number
${f_\gamma }\!\left( \cdot \right)$, there exists a number ![]() ${x_1} \in \left( {\vartheta ,{x_\gamma }} \right)$ such that
${x_1} \in \left( {\vartheta ,{x_\gamma }} \right)$ such that
Besides, integrating (14) with respect to ![]() $x$ from
$x$ from ![]() ${x_1}$ to
${x_1}$ to ![]() ${x_\gamma }$, we have
${x_\gamma }$, we have
 \begin{align*}&\left( {{\gamma _2} - {\gamma _1}} \right) \cdot \left( {{x_\gamma } - {x_1}} \right) \\[5pt]
&\qquad= \frac{1}{2}{\sigma ^2}\!\left( {{f_\gamma }\!\left( {{x_\gamma }} \right) - {f_\gamma }\!\left( {{x_1}} \right)} \right) + \mathop \int \nolimits_{{x_1}}^{{x_\gamma }} \!\left[ {\pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _2}} \right)} \right) - \pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _1}} \right)} \right)} \right]{\rm{d}}y\\[5pt]
&\qquad\lt \mathop \int \nolimits_{{x_1}}^{{x_\gamma }} \!\left[ {\pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _2}} \right)} \right) - \pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _1}} \right)} \right)} \right]{\rm{d}}y\\[5pt]
&\qquad \le \mathop \int \nolimits_{{x_1}}^{{x_\gamma }} M{f_\gamma }\!\left( y \right){\rm{d}}y\\[5pt]
& \qquad \le \!\left( {{\gamma _2} - {\gamma _1}} \right) \cdot \left( {{x_\gamma } - {x_1}} \right),\end{align*}
\begin{align*}&\left( {{\gamma _2} - {\gamma _1}} \right) \cdot \left( {{x_\gamma } - {x_1}} \right) \\[5pt]
&\qquad= \frac{1}{2}{\sigma ^2}\!\left( {{f_\gamma }\!\left( {{x_\gamma }} \right) - {f_\gamma }\!\left( {{x_1}} \right)} \right) + \mathop \int \nolimits_{{x_1}}^{{x_\gamma }} \!\left[ {\pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _2}} \right)} \right) - \pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _1}} \right)} \right)} \right]{\rm{d}}y\\[5pt]
&\qquad\lt \mathop \int \nolimits_{{x_1}}^{{x_\gamma }} \!\left[ {\pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _2}} \right)} \right) - \pi \!\left( {w\!\left( {y;\,\vartheta ,{\gamma _1}} \right)} \right)} \right]{\rm{d}}y\\[5pt]
&\qquad \le \mathop \int \nolimits_{{x_1}}^{{x_\gamma }} M{f_\gamma }\!\left( y \right){\rm{d}}y\\[5pt]
& \qquad \le \!\left( {{\gamma _2} - {\gamma _1}} \right) \cdot \left( {{x_\gamma } - {x_1}} \right),\end{align*}
where the first and the last inequalities follow from Equation (15), and the second inequality follows from Equation (11). This reaches a contradiction.
Next, we prove that ![]() ${\rm{li}}{{\rm{m}}_{\gamma \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ for any fixed
${\rm{li}}{{\rm{m}}_{\gamma \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ for any fixed ![]() $x$ with
$x$ with ![]() $x \gt \vartheta $. Choose
$x \gt \vartheta $. Choose ![]() ${\gamma _3} = \pi (0) + {\rm{ma}}{{\rm{x}}_{y \in \left[ {\vartheta ,x} \right]}}h\!\left( y \right)$. We claim that
${\gamma _3} = \pi (0) + {\rm{ma}}{{\rm{x}}_{y \in \left[ {\vartheta ,x} \right]}}h\!\left( y \right)$. We claim that
In fact, if Equation (16) fails to hold, by the continuity of ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ and the fact that
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ and the fact that ![]() $w\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) = 0$, there must exist a number
$w\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) = 0$, there must exist a number ![]() ${y_1} \in \left[ {\vartheta ,x} \right)$ such that
${y_1} \in \left[ {\vartheta ,x} \right)$ such that ![]() $w\!\left( {{y_1};\, \vartheta ,\gamma } \right) = 0$ and
$w\!\left( {{y_1};\, \vartheta ,\gamma } \right) = 0$ and ![]() $w'\!\left( {{y_1};\, \vartheta ,\gamma } \right) \lt 0$ for some
$w'\!\left( {{y_1};\, \vartheta ,\gamma } \right) \lt 0$ for some ![]() $\gamma \ge {\gamma _3}$. Evaluating (O) at
$\gamma \ge {\gamma _3}$. Evaluating (O) at ![]() ${y_1}$ gives
${y_1}$ gives
This contradiction demonstrates the correctness of Equation (16). As a result, Equation (12) implies that for all ![]() $y \in \left[ {\vartheta ,x} \right]$ and
$y \in \left[ {\vartheta ,x} \right]$ and ![]() $\gamma \ge {\gamma _3}$,
$\gamma \ge {\gamma _3}$,
which in turn gives
for all ![]() $\gamma \ge {\gamma _3}$, where
$\gamma \ge {\gamma _3}$, where ![]() $\xi \,:\!=\, 2M/{\sigma ^2}$. Letting
$\xi \,:\!=\, 2M/{\sigma ^2}$. Letting ![]() $\gamma \to \infty $ in this inequality yields
$\gamma \to \infty $ in this inequality yields ![]() ${\rm{li}}{{\rm{m}}_{\gamma \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $.
${\rm{li}}{{\rm{m}}_{\gamma \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $.
Similar to the above argument, except that now Equation (13) is used instead of Equation (12), one can show that ![]() ${\rm{li}}{{\rm{m}}_{\gamma \to - \infty }}w( {x;\, \vartheta ,\gamma }) = - \infty $. The detailed proof is omitted for brevity.
${\rm{li}}{{\rm{m}}_{\gamma \to - \infty }}w( {x;\, \vartheta ,\gamma }) = - \infty $. The detailed proof is omitted for brevity.
![]() $\left( {{b}} \right)$ The case of
$\left( {{b}} \right)$ The case of ![]() $x \lt \vartheta $ can be treated similarly, and thus its proof is also omitted.
$x \lt \vartheta $ can be treated similarly, and thus its proof is also omitted.
Remark 1. We point out that in the proof, we did not directly differentiate both sides of (O) with respect to ![]() $\gamma $ to obtain the result that
$\gamma $ to obtain the result that ![]() $\partial w( {x;\, \vartheta ,\gamma })/\partial \gamma \gt 0$ for any
$\partial w( {x;\, \vartheta ,\gamma })/\partial \gamma \gt 0$ for any ![]() $x \gt \vartheta $. This is because
$x \gt \vartheta $. This is because ![]() $\pi \!\left( w \right)$ may not be differentiable in
$\pi \!\left( w \right)$ may not be differentiable in ![]() $w$ on its entire domain. Hence, we employ a contradictory argument in the proof.
$w$ on its entire domain. Hence, we employ a contradictory argument in the proof.
The following proposition characterizes the monotonic properties of ![]() $w( {x;\, \vartheta ,\gamma })$ with respect to
$w( {x;\, \vartheta ,\gamma })$ with respect to ![]() $x$. Defining
$x$. Defining
which is well defined, although it might be ![]() $\infty $. (If
$\infty $. (If ![]() $w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all
$w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all ![]() $x \gt \vartheta $ and
$x \gt \vartheta $ and ![]() $\gamma \gt \pi (0) + h(\vartheta)$, we let
$\gamma \gt \pi (0) + h(\vartheta)$, we let ![]() ${\bar \gamma _1}(\vartheta) = \pi (0) + h(\vartheta)$.) Similarly, defining
${\bar \gamma _1}(\vartheta) = \pi (0) + h(\vartheta)$.) Similarly, defining
which is also well defined by allowing it to take value ![]() $\infty $. (If
$\infty $. (If ![]() $w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all
$w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all ![]() $x \lt \vartheta $ and
$x \lt \vartheta $ and ![]() $\gamma \gt \pi (0) + h(\vartheta)$, we let
$\gamma \gt \pi (0) + h(\vartheta)$, we let ![]() ${\bar \gamma _2}(\vartheta) = \pi (0) + h(\vartheta)$.)
${\bar \gamma _2}(\vartheta) = \pi (0) + h(\vartheta)$.)
Proposition 1. Fix ![]() $\vartheta $ and
$\vartheta $ and ![]() $\gamma $ such that
$\gamma $ such that ![]() $\gamma \gt \pi (0) + h(\vartheta)$. There exist two numbers
$\gamma \gt \pi (0) + h(\vartheta)$. There exist two numbers ![]() $x_1^*( {\vartheta ,\gamma })$ (maybe
$x_1^*( {\vartheta ,\gamma })$ (maybe ![]() $\infty $) and
$\infty $) and ![]() $x_2^*( {\vartheta ,\gamma })$ (maybe
$x_2^*( {\vartheta ,\gamma })$ (maybe ![]() $ - \infty $) with
$ - \infty $) with ![]() $x_1^*( {\vartheta ,\gamma }) \gt \vartheta \gt x_2^*( {\vartheta ,\gamma })$ such that the following properties hold:
$x_1^*( {\vartheta ,\gamma }) \gt \vartheta \gt x_2^*( {\vartheta ,\gamma })$ such that the following properties hold:
(i)
 $w( {x;\, \vartheta ,\gamma })$ is decreasing in
$w( {x;\, \vartheta ,\gamma })$ is decreasing in  $x$ on
$x$ on  $\big( { - \infty ,x_2^{\ast} ( {\vartheta ,\gamma } )} \big)$, increasing in
$\big( { - \infty ,x_2^{\ast} ( {\vartheta ,\gamma } )} \big)$, increasing in  $x$ on
$x$ on  $\left( {x_2^{\ast}( {\vartheta ,\gamma }),x_1^{\ast}( {\vartheta ,\gamma })} \right)$ and decreasing in
$\left( {x_2^{\ast}( {\vartheta ,\gamma }),x_1^{\ast}( {\vartheta ,\gamma })} \right)$ and decreasing in  $x$ on
$x$ on  $\big( {x_1^{\ast}( {\vartheta ,\gamma }),\infty }\big)$.
$\big( {x_1^{\ast}( {\vartheta ,\gamma }),\infty }\big)$.-
(ii)
 ${\rm{li}}{{\rm{m}}_{x \to \infty }}w( {x;\, \vartheta ,\gamma }) = - \infty $ if
${\rm{li}}{{\rm{m}}_{x \to \infty }}w( {x;\, \vartheta ,\gamma }) = - \infty $ if  $x_1^{\ast}( {\vartheta ,\gamma }) \lt \infty $, and
$x_1^{\ast}( {\vartheta ,\gamma }) \lt \infty $, and  ${\rm{li}}{{\rm{m}}_{x \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ if
${\rm{li}}{{\rm{m}}_{x \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ if  $x_1^{\ast}( {\vartheta ,\gamma }) = \infty $.
$x_1^{\ast}( {\vartheta ,\gamma }) = \infty $. -
(iii)
 ${\rm{li}}{{\rm{m}}_{x \to - \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ if
${\rm{li}}{{\rm{m}}_{x \to - \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ if  $x_2^{\ast}( {\vartheta ,\gamma }) \gt - \infty $, and
$x_2^{\ast}( {\vartheta ,\gamma }) \gt - \infty $, and  ${\rm{li}}{{\rm{m}}_{x \to - \infty }}w( {x;\, \vartheta ,\gamma }) = - \infty $ if
${\rm{li}}{{\rm{m}}_{x \to - \infty }}w( {x;\, \vartheta ,\gamma }) = - \infty $ if  $x_2^{\ast}( {\vartheta ,\gamma }) = - \infty $.
$x_2^{\ast}( {\vartheta ,\gamma }) = - \infty $. -
(iv)
 $x_1^{\ast}( {\vartheta ,\gamma }) \gt 0 \gt x_2^{\ast}( {\vartheta ,\gamma })$.
$x_1^{\ast}( {\vartheta ,\gamma }) \gt 0 \gt x_2^{\ast}( {\vartheta ,\gamma })$.
Proof. (![]() ${{a}}$) Evaluating (O) at
${{a}}$) Evaluating (O) at ![]() $\vartheta $, we have
$\vartheta $, we have
First, we prove the structural properties for ![]() $x \gt \vartheta $. We claim the following properties:
$x \gt \vartheta $. We claim the following properties:
(i)
 $w( {x;\, \vartheta ,\gamma })$ cannot have a local minimizer in
$w( {x;\, \vartheta ,\gamma })$ cannot have a local minimizer in  $x$ on
$x$ on  $\left( {\vartheta ,\infty } \right)$; and
$\left( {\vartheta ,\infty } \right)$; and-
(ii)
 $w( {x;\, \vartheta ,\gamma })$ cannot be a constant in any interval
$w( {x;\, \vartheta ,\gamma })$ cannot be a constant in any interval  $\left[ {{x_1},{x_2}} \right]$ with
$\left[ {{x_1},{x_2}} \right]$ with  $\vartheta \le {x_1} \lt {x_2}$.
$\vartheta \le {x_1} \lt {x_2}$.
Suppose, to the contradictory, that property (3.1) fails to hold. Then, according to Equation (17), there exist two numbers ![]() ${x_1}$ and
${x_1}$ and ![]() ${x_2}$ with
${x_2}$ with ![]() $\vartheta \lt {x_1} \lt {x_2}$ such that
$\vartheta \lt {x_1} \lt {x_2}$ such that ![]() ${x_1}$ is a local maximizer of
${x_1}$ is a local maximizer of ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ and
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ and ![]() ${x_2}$ is a local minimizer of
${x_2}$ is a local minimizer of ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$. Consequently, there exist four numbers
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$. Consequently, there exist four numbers ![]() ${x_i}$,
${x_i}$, ![]() $i = 3,{\rm{}}4,{\rm{}}5{\rm{\;and\;}}6$ with
$i = 3,{\rm{}}4,{\rm{}}5{\rm{\;and\;}}6$ with ![]() ${x_3} \lt {x_1} \lt {x_4} \lt {x_5} \lt {x_2} \lt {x_6}$ such that (see Figure 1 for an illustration)
${x_3} \lt {x_1} \lt {x_4} \lt {x_5} \lt {x_2} \lt {x_6}$ such that (see Figure 1 for an illustration)

Figure 1. A Graphical Illustration of Function ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ for the Contradictory Argument in the Proof of Proposition 1
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ for the Contradictory Argument in the Proof of Proposition 1
Evaluating (O) at ![]() ${x_3}$ and
${x_3}$ and ![]() ${x_4}$ yields
${x_4}$ yields
which, combining with Equation (18), gives ![]() $h\!\left( {{x_3}} \right) \le h\!\left( {{x_4}} \right)$. Similarly, evaluating (O) at
$h\!\left( {{x_3}} \right) \le h\!\left( {{x_4}} \right)$. Similarly, evaluating (O) at ![]() ${x_5}$ and
${x_5}$ and ![]() ${x_6}$ gives
${x_6}$ gives ![]() $h\!\left( {{x_5}} \right) \ge h\!\left( {{x_6}} \right)$. This makes a contradiction with the quasi-convexity of
$h\!\left( {{x_5}} \right) \ge h\!\left( {{x_6}} \right)$. This makes a contradiction with the quasi-convexity of ![]() $h\!\left( \cdot \right)$, as stated in Assumption 1
$h\!\left( \cdot \right)$, as stated in Assumption 1![]() $(a)$.
$(a)$.
The proof for property (3.1) is much simpler. In fact, if it fails to hold, then there exist two numbers ![]() ${x_1},$ and
${x_1},$ and ![]() ${x_2},$ with
${x_2},$ with ![]() $\vartheta \le {x_1} \lt {x_2},$ such that for any
$\vartheta \le {x_1} \lt {x_2},$ such that for any ![]() $x \in \left( {{x_1},{x_2}} \right)$, we have
$x \in \left( {{x_1},{x_2}} \right)$, we have ![]() $w'( {x;\, \vartheta ,\gamma }) = 0$ and
$w'( {x;\, \vartheta ,\gamma }) = 0$ and ![]() $w( {x;\, \vartheta ,\gamma }) = {w^\dagger }$ for some
$w( {x;\, \vartheta ,\gamma }) = {w^\dagger }$ for some ![]() ${w^\dagger }$. Hence, (O) gives that
${w^\dagger }$. Hence, (O) gives that ![]() $\pi \!\left( {{w^\dagger }} \right) + h(x) = \gamma $ for any
$\pi \!\left( {{w^\dagger }} \right) + h(x) = \gamma $ for any ![]() $x \in \left( {{x_1},{x_2}} \right)$, which contradicts Assumption 1
$x \in \left( {{x_1},{x_2}} \right)$, which contradicts Assumption 1![]() $(a)$.
$(a)$.
If ![]() $\gamma \ge {\bar \gamma _1}(\vartheta)$, then by the definition of
$\gamma \ge {\bar \gamma _1}(\vartheta)$, then by the definition of ![]() ${\bar \gamma _1}(\vartheta)$ and the continuity of
${\bar \gamma _1}(\vartheta)$ and the continuity of ![]() $w'( {x;\, \vartheta ,\gamma })$ in
$w'( {x;\, \vartheta ,\gamma })$ in ![]() $\gamma $, we have
$\gamma $, we have ![]() $w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all
$w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all ![]() $x \ge \vartheta $. Then property (3.1) implies that
$x \ge \vartheta $. Then property (3.1) implies that ![]() $w( {x;\, \vartheta ,\gamma })$ is strictly increasing in
$w( {x;\, \vartheta ,\gamma })$ is strictly increasing in ![]() $x$ on
$x$ on ![]() $\left( {\vartheta ,\infty } \right)$, in which case
$\left( {\vartheta ,\infty } \right)$, in which case ![]() $x_1^{\ast}( {\vartheta ,\gamma }) = \infty $.
$x_1^{\ast}( {\vartheta ,\gamma }) = \infty $.
Now consider the case that ![]() $\gamma \lt {\bar \gamma _1}(\vartheta)$. Define
$\gamma \lt {\bar \gamma _1}(\vartheta)$. Define
Since ![]() $w'\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) \gt 0$ and
$w'\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) \gt 0$ and ![]() $w'( {x;\, \vartheta ,\gamma })$ is continuous in
$w'( {x;\, \vartheta ,\gamma })$ is continuous in ![]() $x$, we have
$x$, we have ![]() $x_1^{\ast}( {\vartheta ,\gamma }) \gt \vartheta $,
$x_1^{\ast}( {\vartheta ,\gamma }) \gt \vartheta $, ![]() $w'( {x;\, \vartheta ,\gamma }) \gt 0$ for
$w'( {x;\, \vartheta ,\gamma }) \gt 0$ for ![]() $x \in \left[ {\vartheta ,x_1^{\ast}( {\vartheta ,\gamma })} \right)$ and
$x \in \left[ {\vartheta ,x_1^{\ast}( {\vartheta ,\gamma })} \right)$ and ![]() $w'\!\left( {{x^{\ast}}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = 0$. Furthermore, properties (1)–(2) imply that
$w'\!\left( {{x^{\ast}}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = 0$. Furthermore, properties (1)–(2) imply that ![]() $w( {x;\, \vartheta ,\gamma })$ is strictly increasing in
$w( {x;\, \vartheta ,\gamma })$ is strictly increasing in ![]() $x$ on
$x$ on ![]() $\left( {\vartheta ,x_1^{\ast}( {\vartheta ,\gamma })} \right)$ and strictly decreasing in
$\left( {\vartheta ,x_1^{\ast}( {\vartheta ,\gamma })} \right)$ and strictly decreasing in ![]() $x$ on
$x$ on ![]() $( {x_1^{\ast}( {\vartheta ,\gamma }),\infty })$.
$( {x_1^{\ast}( {\vartheta ,\gamma }),\infty })$.
Next, we prove the structural properties for ![]() $x \lt \vartheta $. We claim the following properties:
$x \lt \vartheta $. We claim the following properties:
(iii)
 $w( {x;\, \vartheta ,\gamma })$ cannot have a local maximizer in
$w( {x;\, \vartheta ,\gamma })$ cannot have a local maximizer in  $x$ on
$x$ on  $\left( { - \infty ,\vartheta } \right)$; and
$\left( { - \infty ,\vartheta } \right)$; and-
(iv)
 $w( {x;\, \vartheta ,\gamma })$ cannot be a constant in any interval
$w( {x;\, \vartheta ,\gamma })$ cannot be a constant in any interval  $\left[ {{x_1},{x_2}} \right]$ with
$\left[ {{x_1},{x_2}} \right]$ with  $ - \infty \lt {x_1} \lt {x_2} \le \vartheta $.
$ - \infty \lt {x_1} \lt {x_2} \le \vartheta $.
Since the proof is much similar to that for properties (3.1)–(3.2), we omit it for brevity.
If ![]() $\gamma \ge {\bar \gamma _2}(\vartheta)$ by the definition of
$\gamma \ge {\bar \gamma _2}(\vartheta)$ by the definition of ![]() ${\bar \gamma _2}( \vartheta),$ we have
${\bar \gamma _2}( \vartheta),$ we have ![]() $w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all
$w'( {x;\, \vartheta ,\gamma }) \ge 0$ for all ![]() $x \lt \vartheta $. Then Property (2) implies that
$x \lt \vartheta $. Then Property (2) implies that ![]() $w( {x;\, \vartheta ,\gamma })$ is strictly increasing in
$w( {x;\, \vartheta ,\gamma })$ is strictly increasing in ![]() $x$ on
$x$ on ![]() $\left( { - \infty ,\vartheta } \right)$. In this case,
$\left( { - \infty ,\vartheta } \right)$. In this case, ![]() $x_2^{\ast}( {\vartheta ,\gamma }) = - \infty $.
$x_2^{\ast}( {\vartheta ,\gamma }) = - \infty $.
Now consider the case that ![]() $\gamma \lt {\bar \gamma _2}(\vartheta)$. Define
$\gamma \lt {\bar \gamma _2}(\vartheta)$. Define
Since ![]() $w'\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) \gt 0$ and
$w'\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) \gt 0$ and ![]() $w'( {x;\, \vartheta ,\gamma })$ is continuous in
$w'( {x;\, \vartheta ,\gamma })$ is continuous in ![]() $x$, we have
$x$, we have ![]() $x_2^{\ast}( {\vartheta ,\gamma }) \lt \vartheta $,
$x_2^{\ast}( {\vartheta ,\gamma }) \lt \vartheta $, ![]() $w'( {x;\, \vartheta ,\gamma }) \gt 0$ for
$w'( {x;\, \vartheta ,\gamma }) \gt 0$ for ![]() $x \in \left( {x_2^{\ast}( {\vartheta ,\gamma }),\vartheta } \right)$ and
$x \in \left( {x_2^{\ast}( {\vartheta ,\gamma }),\vartheta } \right)$ and ![]() $w'\big( {x_2^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big) = 0$. Furthermore, properties (3.1)–(3.2) imply that
$w'\big( {x_2^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big) = 0$. Furthermore, properties (3.1)–(3.2) imply that ![]() $w( {x;\, \vartheta ,\gamma })$ is strictly increasing in
$w( {x;\, \vartheta ,\gamma })$ is strictly increasing in ![]() $x$ on
$x$ on ![]() $\left( {x_2^{\ast}( {\vartheta ,\gamma }),\vartheta } \right)$ and strictly decreasing in
$\left( {x_2^{\ast}( {\vartheta ,\gamma }),\vartheta } \right)$ and strictly decreasing in ![]() $x$ on
$x$ on ![]() $( { - \infty ,x_2^{\ast} ( {\vartheta ,\gamma })})$.
$( { - \infty ,x_2^{\ast} ( {\vartheta ,\gamma })})$.
Combining the structural properties for ![]() $x \gt \vartheta $ and for
$x \gt \vartheta $ and for ![]() $x \lt \vartheta $, we obtain the result stated in
$x \lt \vartheta $, we obtain the result stated in ![]() $(a)$.
$(a)$.
(b) We claim that ![]() $\lim_{x\to\infty}w(x;\, \vartheta,\gamma)=-\infty$ if
$\lim_{x\to\infty}w(x;\, \vartheta,\gamma)=-\infty$ if ![]() $x^{\star}_1(\vartheta, \gamma)<\infty$. Otherwise, there exists a finite number
$x^{\star}_1(\vartheta, \gamma)<\infty$. Otherwise, there exists a finite number ![]() $\underline{w}$ such that
$\underline{w}$ such that ![]() $\lim_{x\to\infty}w(x;\, \vartheta,\gamma)=\underline{w}$ and thus
$\lim_{x\to\infty}w(x;\, \vartheta,\gamma)=\underline{w}$ and thus ![]() $\lim_{x\to\infty}w'(x;\, \vartheta,\gamma)=0$. Taking
$\lim_{x\to\infty}w'(x;\, \vartheta,\gamma)=0$. Taking ![]() $x \to \infty $ in (O) yields
$x \to \infty $ in (O) yields ![]() ${\rm{li}}{{\rm{m}}_{x \to \infty }}h(x) = \gamma - \pi \!\left( {\underline w } \right)$, which contradicts Assumption 1
${\rm{li}}{{\rm{m}}_{x \to \infty }}h(x) = \gamma - \pi \!\left( {\underline w } \right)$, which contradicts Assumption 1![]() $\left( {{b}} \right)$.
$\left( {{b}} \right)$.
The other assertion can be shown in a similar vein, whose proof is thus omitted.
(c) This can be shown following the same argument as that for
 $\left( {{b}} \right)$.
$\left( {{b}} \right)$.-
(d) We show that
 $x_1^{\ast}( {\vartheta ,\gamma }) \gt 0$, as the result
$x_1^{\ast}( {\vartheta ,\gamma }) \gt 0$, as the result  $x_2^{\ast}( {\vartheta ,\gamma }) \lt 0$ follows a quite similar argument.
$x_2^{\ast}( {\vartheta ,\gamma }) \lt 0$ follows a quite similar argument.
If ![]() $x_1^{\ast}( {\vartheta ,\gamma }) = \infty $, the result holds trivially. Otherwise, for any
$x_1^{\ast}( {\vartheta ,\gamma }) = \infty $, the result holds trivially. Otherwise, for any ![]() $\varepsilon \gt 0$, there exist two numbers
$\varepsilon \gt 0$, there exist two numbers ![]() ${x_7}$ and
${x_7}$ and ![]() ${x_8}$ with
${x_8}$ with ![]() $x_1^{\ast}( {\vartheta ,\gamma }) - \varepsilon \lt {x_7} \lt x_1^{\ast}( {\vartheta ,\gamma }) \lt {x_8} \lt x_1^{\ast}( {\vartheta ,\gamma }) + \varepsilon $ such that
$x_1^{\ast}( {\vartheta ,\gamma }) - \varepsilon \lt {x_7} \lt x_1^{\ast}( {\vartheta ,\gamma }) \lt {x_8} \lt x_1^{\ast}( {\vartheta ,\gamma }) + \varepsilon $ such that
by part (a) of this lemma. Evaluating (O) at ![]() ${x_7}$ and
${x_7}$ and ![]() ${x_8}$ yields
${x_8}$ yields
which, combined with (19), gives ![]() $h\!\left( {{x_7}} \right) \le h\!\left( {{x_8}} \right)$. By the arbitrariness of
$h\!\left( {{x_7}} \right) \le h\!\left( {{x_8}} \right)$. By the arbitrariness of ![]() $\varepsilon $, we obtain that
$\varepsilon $, we obtain that ![]() $h$ is increasing at
$h$ is increasing at ![]() $x_1^{\ast}( {\vartheta ,\gamma })$, which implies
$x_1^{\ast}( {\vartheta ,\gamma })$, which implies ![]() $x_1^{\ast}( {\vartheta ,\gamma }) \gt 0$ by Assumption 1
$x_1^{\ast}( {\vartheta ,\gamma }) \gt 0$ by Assumption 1![]() $(a)$.
$(a)$.
Figure 2 plots a typical function ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$, demonstrating four possible structures that are consistent with the results stated in Proposition 1. In particular, panel
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$, demonstrating four possible structures that are consistent with the results stated in Proposition 1. In particular, panel ![]() $(a)$ corresponds to the first case, in which both
$(a)$ corresponds to the first case, in which both ![]() $x_1^{\ast}( {\vartheta ,\gamma })$ and
$x_1^{\ast}( {\vartheta ,\gamma })$ and ![]() $x_2^{\ast}( {\vartheta ,\gamma })$ are finite and function
$x_2^{\ast}( {\vartheta ,\gamma })$ are finite and function ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ has three different roots. Moreover,
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ has three different roots. Moreover, ![]() $\vartheta $ is the unique root such that
$\vartheta $ is the unique root such that ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is increasing at it. Panel
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is increasing at it. Panel ![]() $\left( {{b}} \right)$ corresponds to the second case, in which
$\left( {{b}} \right)$ corresponds to the second case, in which ![]() $x_1^{\ast}( {\vartheta ,\gamma }) = \infty $ and one can show that
$x_1^{\ast}( {\vartheta ,\gamma }) = \infty $ and one can show that ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is strictly increasing on
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is strictly increasing on ![]() $\left[ {\vartheta ,\infty } \right)$. Similarly, panel
$\left[ {\vartheta ,\infty } \right)$. Similarly, panel ![]() $(c)$ corresponds to the third case, in which
$(c)$ corresponds to the third case, in which ![]() $x_2^{\ast}( {\vartheta ,\gamma }) = - \infty $ and one can show that
$x_2^{\ast}( {\vartheta ,\gamma }) = - \infty $ and one can show that ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is strictly increasing on
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is strictly increasing on ![]() $\left( { - \infty ,\vartheta } \right]$. Panel
$\left( { - \infty ,\vartheta } \right]$. Panel ![]() $\left( {\rm{d}} \right)$ demonstrates the last case, in which both
$\left( {\rm{d}} \right)$ demonstrates the last case, in which both ![]() $x_1^{\ast}( {\vartheta ,\gamma })$ and
$x_1^{\ast}( {\vartheta ,\gamma })$ and ![]() $x_2^{\ast}( {\vartheta ,\gamma })$ are infinite, so function
$x_2^{\ast}( {\vartheta ,\gamma })$ are infinite, so function ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is strictly increasing on the entire
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ is strictly increasing on the entire ![]() $\mathbb{R}$. As we will see, Conditions (7)–(10) cannot be satisfied in the latter three cases, and thus it suffices to focus on the first case.
$\mathbb{R}$. As we will see, Conditions (7)–(10) cannot be satisfied in the latter three cases, and thus it suffices to focus on the first case.
A monotonic property of ![]() $w( {x;\, \vartheta ,\gamma })$ with respect to
$w( {x;\, \vartheta ,\gamma })$ with respect to ![]() $\vartheta $ also holds, which is described below.
$\vartheta $ also holds, which is described below.

Figure 2. A Graphical Illustration of Four Structures for Function ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$
Lemma 4. For any ![]() $\gamma \gt \pi (0)$, define
$\gamma \gt \pi (0)$, define ![]() $\Theta \!\left( \gamma \right)\,:\!=\, \!\left\{ {\vartheta | \gamma > \pi (0) + h(\vartheta)} \right\}$, which is an open and convex set by Assumption 1(a).
$\Theta \!\left( \gamma \right)\,:\!=\, \!\left\{ {\vartheta | \gamma > \pi (0) + h(\vartheta)} \right\}$, which is an open and convex set by Assumption 1(a).
(i) For any
 ${\vartheta _1} \ne {\vartheta _2}$ in
${\vartheta _1} \ne {\vartheta _2}$ in  $\Theta \!\left( \gamma \right)$, functions
$\Theta \!\left( \gamma \right)$, functions  $w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$ and
$w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$ and  $w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$ have no intersection.
$w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$ have no intersection.-
(ii) For any
 $x$,
$x$,  $w( {x;\, \vartheta ,\gamma })$ is strictly decreasing in
$w( {x;\, \vartheta ,\gamma })$ is strictly decreasing in  $\vartheta $ on
$\vartheta $ on  $\Theta \!\left( \gamma \right)$.
$\Theta \!\left( \gamma \right)$.
Proof. ![]() $(a)$ Suppose, to the contradictory, that there exists a point
$(a)$ Suppose, to the contradictory, that there exists a point ![]() ${x_0}$ such that
${x_0}$ such that ![]() $w\!\left( {{x_0};\,{\vartheta _1},\gamma } \right) = w\!\left( {{x_0};\,{\vartheta _2},\gamma } \right)\,:\!=\, {w_0}$. Then both functions
$w\!\left( {{x_0};\,{\vartheta _1},\gamma } \right) = w\!\left( {{x_0};\,{\vartheta _2},\gamma } \right)\,:\!=\, {w_0}$. Then both functions ![]() $w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$ and
$w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$ and ![]() $w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$ are solutions to the problem
$w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$ are solutions to the problem
Similar to the proof of Lemma 2![]() $(a)$, we can show that the above problem has a unique solution, which implies that
$(a)$, we can show that the above problem has a unique solution, which implies that ![]() $w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right) = w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$. Observe from Proposition 1
$w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right) = w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$. Observe from Proposition 1![]() $(a)$ that for any
$(a)$ that for any ![]() $\gamma \gt \pi (0) + h(\vartheta)$, there exist at most three roots of
$\gamma \gt \pi (0) + h(\vartheta)$, there exist at most three roots of ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$, where
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$, where ![]() $\vartheta $ is the only root at which
$\vartheta $ is the only root at which ![]() $w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ has a positive derivative. However, both
$w\!\left( { \cdot ;\,\vartheta ,\gamma } \right)$ has a positive derivative. However, both ![]() ${\vartheta _1}$ and
${\vartheta _1}$ and ![]() ${\vartheta _2}$ are roots of
${\vartheta _2}$ are roots of ![]() $w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right) = w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$, with the corresponding derivatives being positive. This contradiction concludes the result stated in
$w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right) = w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$, with the corresponding derivatives being positive. This contradiction concludes the result stated in ![]() $(a)$.
$(a)$.
(b) This result can be better argued with the help of Figure 2. Consider any ![]() ${\vartheta _1},{\vartheta _2} \in {\rm{\Theta }}\!\left( \gamma \right)$ such that
${\vartheta _1},{\vartheta _2} \in {\rm{\Theta }}\!\left( \gamma \right)$ such that ![]() ${\vartheta _1} \lt {\vartheta _2}$. We will consider only the case of
${\vartheta _1} \lt {\vartheta _2}$. We will consider only the case of ![]() ${\vartheta _1}$ such that panel
${\vartheta _1}$ such that panel ![]() $(a)$ takes place for illustration, as the other three cases can be discussed similarly (with the corresponding arguments simpler). Define
$(a)$ takes place for illustration, as the other three cases can be discussed similarly (with the corresponding arguments simpler). Define ![]() ${x_r}\,:\!=\, {\rm{inf}}\{ x \gt {\vartheta _1}|w\!\left( {x;\,{\vartheta _1},\gamma } \right) \le 0\} $. That is,
${x_r}\,:\!=\, {\rm{inf}}\{ x \gt {\vartheta _1}|w\!\left( {x;\,{\vartheta _1},\gamma } \right) \le 0\} $. That is, ![]() ${x_r}$ is the largest root of function
${x_r}$ is the largest root of function ![]() $w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$. If
$w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$. If ![]() ${\vartheta _2} \in \left( {{\vartheta _1},{x_r}} \right)$, it is clear that function
${\vartheta _2} \in \left( {{\vartheta _1},{x_r}} \right)$, it is clear that function ![]() $w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$ should be strictly below function
$w\!\left( { \cdot ;\,{\vartheta _2},\gamma } \right)$ should be strictly below function ![]() $w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$; otherwise, there will be an intersection between these functions, contradicting
$w\!\left( { \cdot ;\,{\vartheta _1},\gamma } \right)$; otherwise, there will be an intersection between these functions, contradicting ![]() $(a)$. (This argument also rules out the case that
$(a)$. (This argument also rules out the case that ![]() ${\vartheta _2} = {x_r}$.)
${\vartheta _2} = {x_r}$.)
It remains to show that it is impossible for ![]() ${\vartheta _2} \gt {x_r}$. In fact, evaluating (O) at
${\vartheta _2} \gt {x_r}$. In fact, evaluating (O) at ![]() ${x_r}$, we obtain that
${x_r}$, we obtain that
which, combining with ![]() $w'\!\left( {{x_r};\,{\vartheta _1},\gamma } \right) \lt 0$, gives
$w'\!\left( {{x_r};\,{\vartheta _1},\gamma } \right) \lt 0$, gives ![]() $h\!\left( {{x_r}} \right) \gt r - h(0)$, and thus
$h\!\left( {{x_r}} \right) \gt r - h(0)$, and thus ![]() ${x_r} \notin {\rm{\Theta }}\!\left( \gamma \right)$. The result,
${x_r} \notin {\rm{\Theta }}\!\left( \gamma \right)$. The result, ![]() ${\vartheta _2} \gt {x_r}$, will reach a contradiction with
${\vartheta _2} \gt {x_r}$, will reach a contradiction with ![]() ${\vartheta _2} \in {\rm{\Theta }}\!\left( \gamma \right)$ and the convexity of the set
${\vartheta _2} \in {\rm{\Theta }}\!\left( \gamma \right)$ and the convexity of the set ![]() ${\rm{\Theta }}\!\left( \gamma \right)$.
${\rm{\Theta }}\!\left( \gamma \right)$.
At the end of this subsection, we present some other properties of ![]() $w( {x;\, \vartheta ,\gamma })$, which will be used in the consequent analysis.
$w( {x;\, \vartheta ,\gamma })$, which will be used in the consequent analysis.
Lemma 5. Fix ![]() $\vartheta $ and
$\vartheta $ and ![]() $\gamma $ such that
$\gamma $ such that ![]() $\gamma \gt \pi (0) + h(\vartheta)$.
$\gamma \gt \pi (0) + h(\vartheta)$.
(i) Let
 ${\eta _1}( {\vartheta ,\gamma })\,:\!=\, inf\{ x \gt \vartheta |h(x) \ge \gamma - \pi (0)\} $. Then we have that
${\eta _1}( {\vartheta ,\gamma })\,:\!=\, inf\{ x \gt \vartheta |h(x) \ge \gamma - \pi (0)\} $. Then we have that  $w( {x;\, \vartheta ,\gamma }) \gt 0$ for any
$w( {x;\, \vartheta ,\gamma }) \gt 0$ for any  $x \in \left( {\vartheta ,{\eta _1}( {\vartheta ,\gamma })} \right]$.
$x \in \left( {\vartheta ,{\eta _1}( {\vartheta ,\gamma })} \right]$.-
(ii) Let
 ${\eta _2}( {\vartheta ,\gamma })\,:\!=\, sup\!\left\{ {x\!\left\langle \vartheta \right|h(x) \ge \gamma - \pi (0)} \right\}$. Then we have that
${\eta _2}( {\vartheta ,\gamma })\,:\!=\, sup\!\left\{ {x\!\left\langle \vartheta \right|h(x) \ge \gamma - \pi (0)} \right\}$. Then we have that  $w( {x;\, \vartheta ,\gamma }) \lt 0$ for any
$w( {x;\, \vartheta ,\gamma }) \lt 0$ for any  $x \in \left[ {{\eta _2}( {\vartheta ,\gamma }),\vartheta } \right)$.
$x \in \left[ {{\eta _2}( {\vartheta ,\gamma }),\vartheta } \right)$.
Proof. We show only the first assertion, as the second assertion can be proved in a similar way. Suppose, to the contradictory, that there exists a number ![]() ${x_0} \in \left( {\vartheta ,{\eta _1}( {\vartheta ,\gamma })} \right]$ such that
${x_0} \in \left( {\vartheta ,{\eta _1}( {\vartheta ,\gamma })} \right]$ such that ![]() $w\!\left( {{x_0};\,\vartheta ,\gamma } \right) \le 0$. Then a number
$w\!\left( {{x_0};\,\vartheta ,\gamma } \right) \le 0$. Then a number ![]() ${x_1} \in \left( {\vartheta ,{x_0}} \right]$ exists such that
${x_1} \in \left( {\vartheta ,{x_0}} \right]$ exists such that ![]() $w\!\left( {{x_1};\,\vartheta ,\gamma } \right) = 0$ and
$w\!\left( {{x_1};\,\vartheta ,\gamma } \right) = 0$ and ![]() $w'\!\left( {{x_1};\,\vartheta ,\gamma } \right) \lt 0$. Hence, it follows from (O) at
$w'\!\left( {{x_1};\,\vartheta ,\gamma } \right) \lt 0$. Hence, it follows from (O) at ![]() ${x_1}$ that
${x_1}$ that
reaching a contradiction with the definition of ![]() ${\eta _1}( {\vartheta ,\gamma })$.
${\eta _1}( {\vartheta ,\gamma })$.
3.2. Determining the Optimal Parameters
In the previous subsection, we obtained structural and asymptotical properties of solution ![]() $w( {x;\, \vartheta ,\gamma })$ to problem (O). In this subsection, we use those properties to find the optimal policy parameters
$w( {x;\, \vartheta ,\gamma })$ to problem (O). In this subsection, we use those properties to find the optimal policy parameters ![]() $\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ and the auxiliary parameters
$\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ and the auxiliary parameters ![]() $\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$ such that the boundary conditions (7)–(10) are all satisfied.
$\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$ such that the boundary conditions (7)–(10) are all satisfied.
Specifically, in Proposition 2, we show that for some ![]() $\vartheta $, there exist unique
$\vartheta $, there exist unique ![]() $\gamma _1^{\ast}(\vartheta)$,
$\gamma _1^{\ast}(\vartheta)$, ![]() $Q(\vartheta)$ and
$Q(\vartheta)$ and ![]() $S( \vartheta),$ with
$S( \vartheta),$ with ![]() $\gamma _1^{\ast}(\vartheta) \in \left( {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ and
$\gamma _1^{\ast}(\vartheta) \in \left( {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ and ![]() $\vartheta \lt Q(\vartheta) \lt x_1^{\ast}\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right) \lt S( \vartheta),$ such that
$\vartheta \lt Q(\vartheta) \lt x_1^{\ast}\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right) \lt S( \vartheta),$ such that
Similarly, in Proposition 3, we prove that for some ![]() $\vartheta $, there exist unique
$\vartheta $, there exist unique ![]() $\gamma _2^{\ast}(\vartheta)$,
$\gamma _2^{\ast}(\vartheta)$, ![]() $s(\vartheta)$ and
$s(\vartheta)$ and ![]() $q( \vartheta),$ with
$q( \vartheta),$ with ![]() $\gamma _2^{\ast}(\vartheta) \in \left( {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ and
$\gamma _2^{\ast}(\vartheta) \in \left( {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ and ![]() $s(\vartheta) \lt x_2^{\ast}\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right) \lt q(\vartheta) \lt \vartheta ,$ such that
$s(\vartheta) \lt x_2^{\ast}\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right) \lt q(\vartheta) \lt \vartheta ,$ such that
Finally, in Proposition 4, we show that we can choose a number ![]() ${\vartheta ^{\ast}}$ such that
${\vartheta ^{\ast}}$ such that
Let ![]() ${\gamma ^{\ast}} = \gamma _1^{\ast}( {{\vartheta ^{\ast}}})$,
${\gamma ^{\ast}} = \gamma _1^{\ast}( {{\vartheta ^{\ast}}})$, ![]() ${s^{\ast}} = s( {{\vartheta ^{\ast}}})$,
${s^{\ast}} = s( {{\vartheta ^{\ast}}})$, ![]() ${q^{\ast}} = q( {{\vartheta ^{\ast}}})$,
${q^{\ast}} = q( {{\vartheta ^{\ast}}})$, ![]() ${Q^{\ast}} = Q( {{\vartheta ^{\ast}}})$,
${Q^{\ast}} = Q( {{\vartheta ^{\ast}}})$, ![]() ${S^{\ast}} = S( {{\vartheta ^{\ast}}})$,
${S^{\ast}} = S( {{\vartheta ^{\ast}}})$, ![]() $x_1^{\ast} = x_1^{\ast}\!\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$,
$x_1^{\ast} = x_1^{\ast}\!\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$, ![]() $x_2^{\ast} = x_2^{\ast}\!\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$ and
$x_2^{\ast} = x_2^{\ast}\!\left( {{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$ and ![]() ${w^{\ast}}\!\left( \cdot \right) = w\!\left( { \cdot ;\,{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$. Figure 3 depicts the function
${w^{\ast}}\!\left( \cdot \right) = w\!\left( { \cdot ;\,{\vartheta ^{\ast}},{\gamma ^{\ast}}} \right)$. Figure 3 depicts the function ![]() ${w^{\ast}}\!\left( \cdot \right)$ and these parameters.
${w^{\ast}}\!\left( \cdot \right)$ and these parameters.

Figure 3. An Illustration of Optimal Parameters and the Corresponding Function
Theorem 1 follows immediately by combining Propositions 2–4, whose proof is deferred to the end of this subsection.
Now we proceed to prove Equations (20)–(23) by the following results. Before stating Proposition 2, we introduce an auxiliary function:
which has the following properties:
(i)
 $\underline{w}_1(\vartheta)=0$ for any
$\underline{w}_1(\vartheta)=0$ for any  $\vartheta \gt 0$; and
$\vartheta \gt 0$; and-
(ii) Define
 $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } \,:\!=\, inf\{ \vartheta |{\underline w _1}(\vartheta) \lt \infty \} $, which is well defined (maybe
$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } \,:\!=\, inf\{ \vartheta |{\underline w _1}(\vartheta) \lt \infty \} $, which is well defined (maybe  $ - \infty $). Then
$ - \infty $). Then  $\underline{w}_1(\vartheta)$ is finite and strictly decreasing in
$\underline{w}_1(\vartheta)$ is finite and strictly decreasing in  $\vartheta $ on
$\vartheta $ on  $({\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,0}],$ with
$({\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,0}],$ with  $li{m_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{\underline w _1}(\vartheta) = \infty $.
$li{m_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{\underline w _1}(\vartheta) = \infty $. -
(iii)
 ${\overline {{\rm{}}\gamma } _1}(\vartheta) \gt \pi (0) + h(\vartheta)$ if and only if
${\overline {{\rm{}}\gamma } _1}(\vartheta) \gt \pi (0) + h(\vartheta)$ if and only if  $\vartheta \gt \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $.
$\vartheta \gt \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $.
Proof. ![]() $(a)$ First, we claim that for any
$(a)$ First, we claim that for any ![]() $\vartheta \gt 0$,
$\vartheta \gt 0$, ![]() $\vartheta $ is a local maximizer of function
$\vartheta $ is a local maximizer of function ![]() $w\!\left( { \cdot ;\,\vartheta ,\pi (0) + h(\vartheta)} \right)$. Otherwise, there exists a
$w\!\left( { \cdot ;\,\vartheta ,\pi (0) + h(\vartheta)} \right)$. Otherwise, there exists a ![]() ${x_0} \gt \vartheta $ such that
${x_0} \gt \vartheta $ such that ![]() $w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \gt 0$ for any
$w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \gt 0$ for any ![]() $x \in \left( {\vartheta ,{x_0}} \right],$ or there exists a
$x \in \left( {\vartheta ,{x_0}} \right],$ or there exists a ![]() ${x_1} \in \left[ {0,\vartheta } \right)$ such that
${x_1} \in \left[ {0,\vartheta } \right)$ such that ![]() $w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \gt 0$ for any
$w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \gt 0$ for any ![]() $x \in \left( {{x_1},\vartheta } \right]$. In the former case, according to (13), we have
$x \in \left( {{x_1},\vartheta } \right]$. In the former case, according to (13), we have ![]() $\frac{1}{2}{\sigma ^2}w'( {x;\, \vartheta ,\gamma }) - Mw( {x;\, \vartheta ,\gamma }) + \pi (0) + h(x) \le \pi (0) + h(\vartheta)$ for any
$\frac{1}{2}{\sigma ^2}w'( {x;\, \vartheta ,\gamma }) - Mw( {x;\, \vartheta ,\gamma }) + \pi (0) + h(x) \le \pi (0) + h(\vartheta)$ for any ![]() $x \in \left( {\vartheta ,{x_0}} \right]$. Using a similar argument as that in the proof of Lemma 3
$x \in \left( {\vartheta ,{x_0}} \right]$. Using a similar argument as that in the proof of Lemma 3![]() $(a)$, we have
$(a)$, we have
reaching a contradiction. In the latter case, similarly, we can obtain that ![]() $w\!\left( {{x_1};\,\vartheta ,\pi (0) + h(\vartheta)} \right) \lt 0$, another contradiction. Therefore,
$w\!\left( {{x_1};\,\vartheta ,\pi (0) + h(\vartheta)} \right) \lt 0$, another contradiction. Therefore, ![]() $\vartheta $ is a local maximizer of function
$\vartheta $ is a local maximizer of function ![]() $w\!\left( { \cdot ;\,\vartheta ,\pi (0) + h(\vartheta)} \right)$.
$w\!\left( { \cdot ;\,\vartheta ,\pi (0) + h(\vartheta)} \right)$.
If the claim in ![]() $(a)$ fails to hold, then given the above result, there exist a
$(a)$ fails to hold, then given the above result, there exist a ![]() ${\vartheta _0} \gt 0$ and a
${\vartheta _0} \gt 0$ and a ![]() ${x_2} \gt {\vartheta _0}$ such that
${x_2} \gt {\vartheta _0}$ such that ![]() $w\!\left( {{x_2};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) \gt 0$. Consequently, there exists a number
$w\!\left( {{x_2};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) \gt 0$. Consequently, there exists a number ![]() ${x_3} \in \left[ {{\vartheta _0},{x_2}} \right)$ such that
${x_3} \in \left[ {{\vartheta _0},{x_2}} \right)$ such that ![]() $w\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) = 0$ and
$w\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) = 0$ and ![]() $w'\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) \gt 0$. However, it follows from (O) at
$w'\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) \gt 0$. However, it follows from (O) at ![]() ${x_3},$ with
${x_3},$ with ![]() $( {\vartheta ,\gamma }) = \left( {{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right)$, that
$( {\vartheta ,\gamma }) = \left( {{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right)$, that
 \begin{align*}\pi (0) + h\!\left( {{\vartheta _0}} \right) & = \frac{1}{2}{\sigma ^2}w'\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) + \pi \!\left( {w\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right)} \right) + h\!\left( {{x_3}} \right)\\
& \gt \pi (0) + h( {{x_3}}),\end{align*}
\begin{align*}\pi (0) + h\!\left( {{\vartheta _0}} \right) & = \frac{1}{2}{\sigma ^2}w'\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right) + \pi \!\left( {w\!\left( {{x_3};\,{\vartheta _0},\pi (0) + h\!\left( {{\vartheta _0}} \right)} \right)} \right) + h\!\left( {{x_3}} \right)\\
& \gt \pi (0) + h( {{x_3}}),\end{align*}
which reaches a contradiction with Assumption 1![]() $(a)$.
$(a)$.
![]() $\left( {{b}} \right)$ Consider any
$\left( {{b}} \right)$ Consider any ![]() ${\vartheta _1} \lt {\vartheta _2} \le 0$ such that both
${\vartheta _1} \lt {\vartheta _2} \le 0$ such that both ![]() ${\underline w _1}\!\left( {{\vartheta _1}} \right)$ and
${\underline w _1}\!\left( {{\vartheta _1}} \right)$ and ![]() ${\underline w _1}( {{\vartheta _2}})$ are finite. We claim that
${\underline w _1}( {{\vartheta _2}})$ are finite. We claim that ![]() ${\underline w _1}\!\left( {{\vartheta _1}} \right) \gt {\underline w _1}( {{\vartheta _2}})$. Suppose, to the contradictory, that
${\underline w _1}\!\left( {{\vartheta _1}} \right) \gt {\underline w _1}( {{\vartheta _2}})$. Suppose, to the contradictory, that ![]() ${\underline w _1}\!\left( {{\vartheta _1}} \right) \le {\underline w _1}( {{\vartheta _2}})$. Note from Lemma 5
${\underline w _1}\!\left( {{\vartheta _1}} \right) \le {\underline w _1}( {{\vartheta _2}})$. Note from Lemma 5![]() $(a)$ that
$(a)$ that ![]() $w\!\left( {x;\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) \gt 0$ for any
$w\!\left( {x;\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) \gt 0$ for any ![]() $x \in \left( {{\vartheta _1},0} \right)$ as
$x \in \left( {{\vartheta _1},0} \right)$ as ![]() ${\eta _1}\!\left( {{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) =$
${\eta _1}\!\left( {{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) =$ ![]() ${\rm{inf}}\{ x \gt {\vartheta _1}|h(x) \ge h\!\left( {{\vartheta _1}} \right)\} \gt 0$. Hence, if we let
${\rm{inf}}\{ x \gt {\vartheta _1}|h(x) \ge h\!\left( {{\vartheta _1}} \right)\} \gt 0$. Hence, if we let ![]() $\psi (x)\,:\!=\, w\!\left( {x;\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) - w ( x;\,{\vartheta _2},$
$\psi (x)\,:\!=\, w\!\left( {x;\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) - w ( x;\,{\vartheta _2},$ ![]() $\pi (0) +h ( {{\vartheta _2}}))$, then we have
$\pi (0) +h ( {{\vartheta _2}}))$, then we have ![]() $\psi ( {{\vartheta _2}}) \gt 0$. Besides,
$\psi ( {{\vartheta _2}}) \gt 0$. Besides, ![]() $\psi \!\left( {x_1^{\ast}\!\left( {{\vartheta _2},\gamma } \right)} \right) \le {\underline w _1}\!\left( {{\vartheta _1}} \right) - {\underline w _1}( {{\vartheta _2}}) \le 0$. Therefore, there exists a number
$\psi \!\left( {x_1^{\ast}\!\left( {{\vartheta _2},\gamma } \right)} \right) \le {\underline w _1}\!\left( {{\vartheta _1}} \right) - {\underline w _1}( {{\vartheta _2}}) \le 0$. Therefore, there exists a number ![]() ${x_4} \in \left( {{\vartheta _2},x_1^{\ast}\!\left( {{\vartheta _2},\gamma } \right)} \right]$ such that
${x_4} \in \left( {{\vartheta _2},x_1^{\ast}\!\left( {{\vartheta _2},\gamma } \right)} \right]$ such that ![]() $\psi \!\left( {{x_4}} \right) = 0$ and
$\psi \!\left( {{x_4}} \right) = 0$ and ![]() $\psi '\!\left( {{x_4}} \right) \le 0$. That is,
$\psi '\!\left( {{x_4}} \right) \le 0$. That is, ![]() $w\!\left( {{x_4};\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) = w\!\left( {{x_4};\;{\vartheta _2},\pi (0) + h( {{\vartheta _2}})} \right)$ and
$w\!\left( {{x_4};\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) = w\!\left( {{x_4};\;{\vartheta _2},\pi (0) + h( {{\vartheta _2}})} \right)$ and ![]() $w'\!\left( {{x_4};\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) \le w'\!\left( {{x_4};\,{\vartheta _2},\pi (0) + h( {{\vartheta _2}})} \right)$. As a result, we have
$w'\!\left( {{x_4};\,{\vartheta _1},\pi (0) + h\!\left( {{\vartheta _1}} \right)} \right) \le w'\!\left( {{x_4};\,{\vartheta _2},\pi (0) + h( {{\vartheta _2}})} \right)$. As a result, we have
which again reaches a contradiction with Assumption 1![]() $(a)$. The above argument demonstrates that
$(a)$. The above argument demonstrates that ![]() $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $ is well defined; in addition,
$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $ is well defined; in addition, ![]() ${\underline w _1}(\vartheta)$ is finite and strictly decreasing in
${\underline w _1}(\vartheta)$ is finite and strictly decreasing in ![]() $\vartheta $ on
$\vartheta $ on ![]() $( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,0}]$.
$( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,0}]$.
It remains to show that ![]() ${\rm{li}}{{\rm{m}}_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{\underline w _1}(\vartheta) = \infty $. If
${\rm{li}}{{\rm{m}}_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{\underline w _1}(\vartheta) = \infty $. If ![]() $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } \ne - \infty $, it trivially holds by the definition of
$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } \ne - \infty $, it trivially holds by the definition of ![]() $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $. If not, we will show it using a minor modification of the argument for showing that
$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $. If not, we will show it using a minor modification of the argument for showing that ![]() ${\rm{li}}{{\rm{m}}_{\gamma \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ in the proof of Lemma 3
${\rm{li}}{{\rm{m}}_{\gamma \to \infty }}w( {x;\, \vartheta ,\gamma }) = \infty $ in the proof of Lemma 3![]() $(a)$. Again, by Lemma 5
$(a)$. Again, by Lemma 5![]() $(a)$, we have
$(a)$, we have ![]() $w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \gt 0$ for any
$w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \gt 0$ for any ![]() $x \in \left( {\vartheta ,0} \right)$, given that
$x \in \left( {\vartheta ,0} \right)$, given that ![]() $\vartheta \lt 0$. Therefore, a similar argument will give us
$\vartheta \lt 0$. Therefore, a similar argument will give us
Fix any ![]() ${\vartheta _3} \lt 0$ and
${\vartheta _3} \lt 0$ and ![]() ${h_0} \gt 0$. By Assumption 1, there exists a
${h_0} \gt 0$. By Assumption 1, there exists a ![]() ${\vartheta _4} \lt {\vartheta _3}$ such that
${\vartheta _4} \lt {\vartheta _3}$ such that ![]() $h(\vartheta) \gt {h_0} + h\!\left( {{\vartheta _3}} \right)$ for any
$h(\vartheta) \gt {h_0} + h\!\left( {{\vartheta _3}} \right)$ for any ![]() $\vartheta \le {\vartheta _4}$. Hence, for any
$\vartheta \le {\vartheta _4}$. Hence, for any ![]() $\vartheta \le {\vartheta _4}$, the above displayed inequality gives
$\vartheta \le {\vartheta _4}$, the above displayed inequality gives
By the arbitrariness of ![]() ${h_0}$, we have
${h_0}$, we have ![]() ${\rm{li}}{{\rm{m}}_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{\underline w _1}(\vartheta) = {\rm{li}}{{\rm{m}}_{\vartheta \downarrow - \infty }}{\underline w _1}(\vartheta) = \infty $.
${\rm{li}}{{\rm{m}}_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{\underline w _1}(\vartheta) = {\rm{li}}{{\rm{m}}_{\vartheta \downarrow - \infty }}{\underline w _1}(\vartheta) = \infty $.
![]() $(c)$ By the definition of
$(c)$ By the definition of ![]() ${\bar \gamma _1}(\vartheta)$ and Proposition 1,
${\bar \gamma _1}(\vartheta)$ and Proposition 1, ![]() ${\bar \gamma _1}(\vartheta) \gt \pi (0) + h(\vartheta)$ if and only if both
${\bar \gamma _1}(\vartheta) \gt \pi (0) + h(\vartheta)$ if and only if both ![]() $x_1^{\ast}( {\vartheta ,\gamma })$ and
$x_1^{\ast}( {\vartheta ,\gamma })$ and ![]() $w\big( {x_1^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big)$ are finite as
$w\big( {x_1^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big)$ are finite as ![]() $\gamma \downarrow \pi (0) + h(\vartheta)$, which is equivalent to the finiteness of
$\gamma \downarrow \pi (0) + h(\vartheta)$, which is equivalent to the finiteness of ![]() ${\underline w _1}(\vartheta)$. Hence, the desired result follows from
${\underline w _1}(\vartheta)$. Hence, the desired result follows from ![]() $\left( {{b}} \right)$.
$\left( {{b}} \right)$.
(i) For any
 $\vartheta \gt \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $, there exists a finite number
$\vartheta \gt \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $, there exists a finite number  ${\gamma _1}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ such that for any
${\gamma _1}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ such that for any  $\gamma \in \left[ {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$, there are two unique and finite numbers
$\gamma \in \left[ {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$, there are two unique and finite numbers  $Q( {\vartheta ,\gamma })$ and
$Q( {\vartheta ,\gamma })$ and  $S( {\vartheta ,\gamma }),$ with
$S( {\vartheta ,\gamma }),$ with  $\vartheta \lt Q( {\vartheta ,\gamma }) \le x_1^{\ast}( {\vartheta ,\gamma }) \le S( {\vartheta ,\gamma }),$ satisfying
$\vartheta \lt Q( {\vartheta ,\gamma }) \le x_1^{\ast}( {\vartheta ,\gamma }) \le S( {\vartheta ,\gamma }),$ satisfying
 \begin{align*}w\!\left( {Q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {S( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = \ell.\end{align*}
\begin{align*}w\!\left( {Q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {S( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = \ell.\end{align*}
-
(ii) There exists a number
 $\underline \vartheta \in \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,0} \right)$ such that for any
$\underline \vartheta \in \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,0} \right)$ such that for any  $\vartheta \ge \underline \vartheta $, there is a unique finite number
$\vartheta \ge \underline \vartheta $, there is a unique finite number  $\gamma _1^*(\vartheta) \in \left[ {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ such that
(25)where
$\gamma _1^*(\vartheta) \in \left[ {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ such that
(25)where \begin{align}{f_1}\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right) = L,\end{align}
is strictly increasing in
\begin{align}{f_1}\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right) = L,\end{align}
is strictly increasing in \begin{align*}{f_1}( {\vartheta ,\gamma })\,:\!=\, \mathop \int \nolimits_\vartheta ^\infty {\rm{max}}\!\left\{ {w( {x;\, \vartheta ,\gamma }) - \ell ,0} \right\}{\rm{d}}x\end{align*}
\begin{align*}{f_1}( {\vartheta ,\gamma })\,:\!=\, \mathop \int \nolimits_\vartheta ^\infty {\rm{max}}\!\left\{ {w( {x;\, \vartheta ,\gamma }) - \ell ,0} \right\}{\rm{d}}x\end{align*}
 $\gamma $ on
$\gamma $ on  $\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$.
$\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$.
(iii)
 $\gamma _1^{\ast}(\vartheta)$ is continuous and strictly increasing in
$\gamma _1^{\ast}(\vartheta)$ is continuous and strictly increasing in  $\vartheta $ on
$\vartheta $ on  $\left[ {\underline \vartheta ,\infty } \right)$, with
$\left[ {\underline \vartheta ,\infty } \right)$, with  $\gamma _1^{\ast}\!\left( {\underline \vartheta } \right) = \pi (0) + h\!\left( {\underline \vartheta } \right)$.
$\gamma _1^{\ast}\!\left( {\underline \vartheta } \right) = \pi (0) + h\!\left( {\underline \vartheta } \right)$.
Proof. ![]() $\left( a \right)$ For any
$\left( a \right)$ For any ![]() $\vartheta \gt \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $, define
$\vartheta \gt \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $, define
(It is well defined by Lemma 6![]() $(c)$.) It follows from Proposition 1
$(c)$.) It follows from Proposition 1![]() $(a)$ that
$(a)$ that
which, together with Lemma 3, implies that ![]() $w\big( {x_1^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big)$ is strictly increasing in
$w\big( {x_1^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big)$ is strictly increasing in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$. Furthermore, Proposition 1
$\left( {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$. Furthermore, Proposition 1![]() $\left( {{b}} \right)$ implies that
$\left( {{b}} \right)$ implies that ![]() ${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_1}(\vartheta)}}w\big( {x_1^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big) = \infty.$ Hence,
${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_1}(\vartheta)}}w\big( {x_1^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big) = \infty.$ Hence, ![]() ${\gamma _1}(\vartheta)$ is well defined and finite.
${\gamma _1}(\vartheta)$ is well defined and finite.
Let ![]() ${\underline \vartheta _1}\,:\!=\, {\rm{inf}}\{ \vartheta |{\underline w _1}(\vartheta) \le \ell \} $. By Lemma 6
${\underline \vartheta _1}\,:\!=\, {\rm{inf}}\{ \vartheta |{\underline w _1}(\vartheta) \le \ell \} $. By Lemma 6![]() $(a)$, it is clear that
$(a)$, it is clear that ![]() ${\underline \vartheta _1} \lt 0$. If
${\underline \vartheta _1} \lt 0$. If ![]() $\vartheta \lt {\underline \vartheta _1}$, then we have
$\vartheta \lt {\underline \vartheta _1}$, then we have ![]() ${\gamma _1}(\vartheta) = \pi (0) + h(\vartheta)$, with
${\gamma _1}(\vartheta) = \pi (0) + h(\vartheta)$, with ![]() $w\!\left( {x_1^{\ast}( {\vartheta ,{\gamma _1}(\vartheta)});\,\vartheta ,{\gamma _1}(\vartheta)} \right) \gt l$. If
$w\!\left( {x_1^{\ast}( {\vartheta ,{\gamma _1}(\vartheta)});\,\vartheta ,{\gamma _1}(\vartheta)} \right) \gt l$. If ![]() $\vartheta \ge {\underline \vartheta _1}$, then we have
$\vartheta \ge {\underline \vartheta _1}$, then we have ![]() ${\gamma _1}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ and
${\gamma _1}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ and ![]() $w\!\left( {x_1^{\ast}( {\vartheta ,{\gamma _1}(\vartheta)});\,\vartheta ,{\gamma _1}(\vartheta)} \right) = \ell $. In either case, we have
$w\!\left( {x_1^{\ast}( {\vartheta ,{\gamma _1}(\vartheta)});\,\vartheta ,{\gamma _1}(\vartheta)} \right) = \ell $. In either case, we have
For ![]() $\gamma \in \left( {{\gamma _1}( \vartheta),\bar \gamma (\vartheta)} \right)$, define
$\gamma \in \left( {{\gamma _1}( \vartheta),\bar \gamma (\vartheta)} \right)$, define
Then it follows from Proposition 1 and ![]() $w\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) = 0 \lt \ell $ that both
$w\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) = 0 \lt \ell $ that both ![]() $Q( {\vartheta ,\gamma })$ and
$Q( {\vartheta ,\gamma })$ and ![]() $S( {\vartheta ,\gamma })$ are well defined, finite and unique and thus
$S( {\vartheta ,\gamma })$ are well defined, finite and unique and thus ![]() $\vartheta \lt Q( {\vartheta ,\gamma }) \lt x_1^{\ast}( {\vartheta ,\gamma }) \lt S( {\vartheta ,\gamma })$ and
$\vartheta \lt Q( {\vartheta ,\gamma }) \lt x_1^{\ast}( {\vartheta ,\gamma }) \lt S( {\vartheta ,\gamma })$ and ![]() $w\!\left( {Q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {S( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = \ell $.
$w\!\left( {Q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {S( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = \ell $.
![]() $\left( {{b}} \right)$ It follows from Proposition 1
$\left( {{b}} \right)$ It follows from Proposition 1![]() $(a)$ and the definitions of
$(a)$ and the definitions of ![]() $Q( {\vartheta ,\gamma })$ and
$Q( {\vartheta ,\gamma })$ and ![]() $S( {\vartheta ,\gamma })$ that
$S( {\vartheta ,\gamma })$ that
 \begin{align*}f_1(\vartheta,\gamma)= \left\{
\begin{array}{l@{\quad}l}
0 &\text {for $\gamma\in(\pi(0)+h(\vartheta), \gamma_1(\vartheta)]$},\\
\int_{Q(\vartheta,\gamma)}^{S(\vartheta,\gamma)} \big(w(x;\, \vartheta,\gamma)-\ell \big) \, \mathrm{d}x
& \text{for $\gamma\in(\gamma_1(\vartheta),\bar{\gamma}_1(\vartheta))$},\\
\infty & \text{for $\gamma\in[\bar{\gamma}_1(\vartheta),\infty)$},
\end{array}
\right.
\end{align*}
\begin{align*}f_1(\vartheta,\gamma)= \left\{
\begin{array}{l@{\quad}l}
0 &\text {for $\gamma\in(\pi(0)+h(\vartheta), \gamma_1(\vartheta)]$},\\
\int_{Q(\vartheta,\gamma)}^{S(\vartheta,\gamma)} \big(w(x;\, \vartheta,\gamma)-\ell \big) \, \mathrm{d}x
& \text{for $\gamma\in(\gamma_1(\vartheta),\bar{\gamma}_1(\vartheta))$},\\
\infty & \text{for $\gamma\in[\bar{\gamma}_1(\vartheta),\infty)$},
\end{array}
\right.
\end{align*}
for any ![]() $( {\vartheta ,\gamma })$ such that
$( {\vartheta ,\gamma })$ such that ![]() $\vartheta \gt \hat{\vartheta}$ and
$\vartheta \gt \hat{\vartheta}$ and ![]() $\gamma \gt \pi (0) + h(\vartheta)$.
$\gamma \gt \pi (0) + h(\vartheta)$.
Hence, by Lemma 3![]() $(a)$, we obtain that
$(a)$, we obtain that ![]() ${f_1}\!\left( {\vartheta,\gamma } \right)$ is strictly increasing in
${f_1}\!\left( {\vartheta,\gamma } \right)$ is strictly increasing in ![]() $\gamma $ on
$\gamma $ on ![]() $\left[ {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$. Besides, we have
$\left[ {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$. Besides, we have ![]() ${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_1}(\vartheta)}}{f_1}( {\vartheta ,\gamma }) = \infty $.
${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_1}(\vartheta)}}{f_1}( {\vartheta ,\gamma }) = \infty $.
If ![]() $\vartheta \ge {\underline \vartheta _1}$, then we have
$\vartheta \ge {\underline \vartheta _1}$, then we have ![]() ${\rm{li}}{{\rm{m}}_{\gamma \downarrow {\gamma _1}(\vartheta)}}{f_1}( {\vartheta ,\gamma }) = 0$. If
${\rm{li}}{{\rm{m}}_{\gamma \downarrow {\gamma _1}(\vartheta)}}{f_1}( {\vartheta ,\gamma }) = 0$. If ![]() $\vartheta \in ( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,{{\underline \vartheta }_1}})$, then
$\vartheta \in ( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } ,{{\underline \vartheta }_1}})$, then ![]() ${\rm{li}}{{\rm{m}}_{\gamma \downarrow {\gamma _1}(\vartheta)}}{f_1}( {\vartheta ,\gamma }) = {f_1}\!\left( {\vartheta ,\pi (0) + h(\vartheta)} \right)$.
${\rm{li}}{{\rm{m}}_{\gamma \downarrow {\gamma _1}(\vartheta)}}{f_1}( {\vartheta ,\gamma }) = {f_1}\!\left( {\vartheta ,\pi (0) + h(\vartheta)} \right)$.
Define
which is well defined, as we can show that (i) ![]() ${f_1}\!\left( {{{\underline \vartheta }_1},\pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)} \right) = 0$ and (ii)
${f_1}\!\left( {{{\underline \vartheta }_1},\pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)} \right) = 0$ and (ii) ![]() ${\rm{li}}{{\rm{m}}_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{f_1}\!\left( {\vartheta ,\pi (0) + h(\vartheta)} \right) = \infty $. In fact, the relation (i) follows by noting that
${\rm{li}}{{\rm{m}}_{\vartheta \downarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } }}{f_1}\!\left( {\vartheta ,\pi (0) + h(\vartheta)} \right) = \infty $. In fact, the relation (i) follows by noting that ![]() ${\gamma _1}\!\left( {{{\underline \vartheta }_1}} \right) = \pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)$ by the discussion after the definition of
${\gamma _1}\!\left( {{{\underline \vartheta }_1}} \right) = \pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)$ by the discussion after the definition of ![]() ${\underline \vartheta _1}$, which further implies
${\underline \vartheta _1}$, which further implies ![]() $Q\!\left( {{{\underline \vartheta }_1},\pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)} \right) = S\!\left( {{{\underline \vartheta }_1},\pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)} \right)$. If
$Q\!\left( {{{\underline \vartheta }_1},\pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)} \right) = S\!\left( {{{\underline \vartheta }_1},\pi (0) + h\!\left( {{{\underline \vartheta }_1}} \right)} \right)$. If ![]() $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } \ne - \infty $, relation (ii) trivially holds by the definition of
$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } \ne - \infty $, relation (ii) trivially holds by the definition of ![]() $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $. If not, using a similar argument yielding (25), we can show that for any
$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } $. If not, using a similar argument yielding (25), we can show that for any ![]() ${h_0} \gt 0$ and
${h_0} \gt 0$ and ![]() ${\vartheta ^\dagger } \lt - 1$, there exists a
${\vartheta ^\dagger } \lt - 1$, there exists a ![]() ${\vartheta ^{\dagger \dagger }} \lt {\vartheta ^\dagger }$ such that for any
${\vartheta ^{\dagger \dagger }} \lt {\vartheta ^\dagger }$ such that for any ![]() $\vartheta \in \left( { - \infty ,{\vartheta ^{\dagger \dagger }}} \right]$, it holds that
$\vartheta \in \left( { - \infty ,{\vartheta ^{\dagger \dagger }}} \right]$, it holds that
 \begin{align*}w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \ge \frac{{2{h_0}\!\left( {1 - {e^{\xi \!\left( {{\vartheta ^\dagger }{\rm{}} - {\rm{}}x} \right)}}} \right)}}{{{\sigma ^2}\xi }} \ge \frac{{2{h_0}\!\left( {1 - {e^{\xi \!\left( {{\vartheta ^\dagger } + 1} \right)}}} \right)}}{{{\sigma ^2}\xi }} \forall x \in \left[ { - 1,0} \right].\end{align*}
\begin{align*}w\!\left( {x;\, \vartheta ,\pi (0) + h(\vartheta)} \right) \ge \frac{{2{h_0}\!\left( {1 - {e^{\xi \!\left( {{\vartheta ^\dagger }{\rm{}} - {\rm{}}x} \right)}}} \right)}}{{{\sigma ^2}\xi }} \ge \frac{{2{h_0}\!\left( {1 - {e^{\xi \!\left( {{\vartheta ^\dagger } + 1} \right)}}} \right)}}{{{\sigma ^2}\xi }} \forall x \in \left[ { - 1,0} \right].\end{align*}
As a result, we have
 \begin{align*} &f_1(\vartheta, \pi(0)+h(\vartheta)) \ge \int_{-1}^0 \max\{w(x;\, \vartheta, \pi(0)+h(\vartheta)) -\ell\} dx
\\
&\quad \ge \int_{-1}^0\max\!\Big\{\frac{2h_0 (1- e^{\xi (\vartheta^\dagger+1)})}{\sigma^2 \xi}-\ell, 0 \Big\} dx.
\end{align*}
\begin{align*} &f_1(\vartheta, \pi(0)+h(\vartheta)) \ge \int_{-1}^0 \max\{w(x;\, \vartheta, \pi(0)+h(\vartheta)) -\ell\} dx
\\
&\quad \ge \int_{-1}^0\max\!\Big\{\frac{2h_0 (1- e^{\xi (\vartheta^\dagger+1)})}{\sigma^2 \xi}-\ell, 0 \Big\} dx.
\end{align*}
By the arbitrariness of ![]() ${h_0}$, we obtain (ii).
${h_0}$, we obtain (ii).
Clearly, ![]() $\underline \vartheta \lt 0$ since
$\underline \vartheta \lt 0$ since ![]() ${\underline \vartheta _1} \lt 0$. It follows from the continuity of
${\underline \vartheta _1} \lt 0$. It follows from the continuity of ![]() ${f_1}( {\vartheta ,\gamma })$ in
${f_1}( {\vartheta ,\gamma })$ in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ (the continuity of
$\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ (the continuity of ![]() ${f_1}( {\vartheta ,\gamma })$ is implied by the continuity of
${f_1}( {\vartheta ,\gamma })$ is implied by the continuity of ![]() $w( {x;\, \vartheta ,\gamma })$) that for any
$w( {x;\, \vartheta ,\gamma })$) that for any ![]() $\vartheta \ge \underline \vartheta $, there exists a unique
$\vartheta \ge \underline \vartheta $, there exists a unique ![]() $\gamma _1^{\ast}(\vartheta) \in \left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ such that
$\gamma _1^{\ast}(\vartheta) \in \left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$ such that ![]() ${f_1}\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right) = L$.
${f_1}\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right) = L$.
![]() $(c)$ By the definition of
$(c)$ By the definition of ![]() $\underline \vartheta $, we have
$\underline \vartheta $, we have ![]() $\gamma _1^{\ast}\!\left( {\underline \vartheta } \right) = \pi (0) + h\!\left( {\underline \vartheta } \right)$. That
$\gamma _1^{\ast}\!\left( {\underline \vartheta } \right) = \pi (0) + h\!\left( {\underline \vartheta } \right)$. That ![]() $\gamma _1^{\ast}(\vartheta)$ is continuous in
$\gamma _1^{\ast}(\vartheta)$ is continuous in ![]() $\vartheta $ follows from the monotonicity of
$\vartheta $ follows from the monotonicity of ![]() ${f_1}( {\vartheta ,\gamma })$ in
${f_1}( {\vartheta ,\gamma })$ in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$, the continuity of
$\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$, the continuity of ![]() ${f_1}( {\vartheta ,\gamma })$ in
${f_1}( {\vartheta ,\gamma })$ in ![]() $\vartheta $ and the implicit function theorem (see e.g. Theorem 1.1 in [Reference Kumagai24]). It remains to show that
$\vartheta $ and the implicit function theorem (see e.g. Theorem 1.1 in [Reference Kumagai24]). It remains to show that ![]() $\gamma _1^{\ast}(\vartheta)$ is strictly increasing in
$\gamma _1^{\ast}(\vartheta)$ is strictly increasing in ![]() $\vartheta $.
$\vartheta $.
Consider any ![]() ${\vartheta _1} \lt {\vartheta _2}$ on
${\vartheta _1} \lt {\vartheta _2}$ on ![]() $[ {\underline \vartheta ,\infty })$. First, we consider the case that
$[ {\underline \vartheta ,\infty })$. First, we consider the case that ![]() ${\vartheta _2} \in {\rm{\Theta }}\!\left( {\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right)$ or, equivalently, that
${\vartheta _2} \in {\rm{\Theta }}\!\left( {\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right)$ or, equivalently, that ![]() $\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right) \gt \pi (0) + h( {{\vartheta _2}})$. By Lemma 4
$\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right) \gt \pi (0) + h( {{\vartheta _2}})$. By Lemma 4![]() $\left( {{b}} \right)$, we have
$\left( {{b}} \right)$, we have ![]() $w\!\left( {x;\,{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) \gt w\!\left( {x;\,{\vartheta _2},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right)$ for any
$w\!\left( {x;\,{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) \gt w\!\left( {x;\,{\vartheta _2},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right)$ for any ![]() $x \ge {\vartheta _2}$. Consequently, we have
$x \ge {\vartheta _2}$. Consequently, we have
 \begin{align*}L & = {f_1}\!\left( {{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) = \mathop \int \nolimits_{{\vartheta _1}}^\infty {\rm{max}}\!\left\{ {w\!\left( {x;\,{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) - \ell ,0} \right\}{\rm{d}}x\\[5pt]
& \ge \mathop \int \nolimits_{{\vartheta _2}}^\infty {\rm{max}}\!\left\{ {w\!\left( {x;\,{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) - \ell ,0} \right\}{\rm{d}}x\\[5pt]
&\gt \mathop \int \nolimits_{{\vartheta _2}}^\infty {\rm{max}}\!\left\{ {w\!\left( {x;\,{\vartheta _2},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) - \ell ,0} \right\}{\rm{d}}x\\[5pt]
& = {f_1}\!\left( {{\vartheta _2},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right).\end{align*}
\begin{align*}L & = {f_1}\!\left( {{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) = \mathop \int \nolimits_{{\vartheta _1}}^\infty {\rm{max}}\!\left\{ {w\!\left( {x;\,{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) - \ell ,0} \right\}{\rm{d}}x\\[5pt]
& \ge \mathop \int \nolimits_{{\vartheta _2}}^\infty {\rm{max}}\!\left\{ {w\!\left( {x;\,{\vartheta _1},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) - \ell ,0} \right\}{\rm{d}}x\\[5pt]
&\gt \mathop \int \nolimits_{{\vartheta _2}}^\infty {\rm{max}}\!\left\{ {w\!\left( {x;\,{\vartheta _2},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right) - \ell ,0} \right\}{\rm{d}}x\\[5pt]
& = {f_1}\!\left( {{\vartheta _2},\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right)} \right).\end{align*}
Hence, ![]() $\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right) \lt \gamma _1^{\ast}( {{\vartheta _2}})$ by noting that
$\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right) \lt \gamma _1^{\ast}( {{\vartheta _2}})$ by noting that ![]() ${f_1}( {\vartheta ,\gamma })$ is strictly increasing in
${f_1}( {\vartheta ,\gamma })$ is strictly increasing in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$.
$\left( {{\gamma _1}( \vartheta),{{\bar \gamma }_1}(\vartheta)} \right)$.
For the case that ![]() $\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right) \le \pi (0) + h\!\left( {_2} \right)$, the result obviously holds by noting that
$\gamma _1^{\ast}\!\left( {{\vartheta _1}} \right) \le \pi (0) + h\!\left( {_2} \right)$, the result obviously holds by noting that ![]() $\gamma _1^{\ast}( {{\vartheta _2}}) \gt \pi (0) + h( {{\vartheta _2}})$.
$\gamma _1^{\ast}( {{\vartheta _2}}) \gt \pi (0) + h( {{\vartheta _2}})$.
Clearly, Equations (20) and (21) are implied by Proposition 2, if we let ![]() $Q(\vartheta) = Q\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right)$ and
$Q(\vartheta) = Q\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right)$ and ![]() $S(\vartheta) = S\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right)$.
$S(\vartheta) = S\!\left( {\vartheta ,\gamma _1^{\ast}(\vartheta)} \right)$.
Similarly, before stating Proposition 3, we introduce an auxiliary function:
which has the following properties. Since the proof follows the same logic as that for Lemma 6, we omit it for brevity.
(i)
 ${\bar w_2}(\vartheta) = 0$ for any
${\bar w_2}(\vartheta) = 0$ for any  $\vartheta \lt 0$; and
$\vartheta \lt 0$; and-
(ii) Define
 $\hat \vartheta \,:\!=\, sup\!\left\{ {\vartheta | {{{\bar w}_2}(\vartheta)} \gt - \infty } \right\}$, which is well defined (maybe
$\hat \vartheta \,:\!=\, sup\!\left\{ {\vartheta | {{{\bar w}_2}(\vartheta)} \gt - \infty } \right\}$, which is well defined (maybe  $\infty $).
$\infty $).  ${\bar w_2}(\vartheta)$ is strictly decreasing in
${\bar w_2}(\vartheta)$ is strictly decreasing in  $\vartheta $ on
$\vartheta $ on  $[ {0,\hat \vartheta }),$ with
$[ {0,\hat \vartheta }),$ with  $li{m_{\vartheta \uparrow \hat \vartheta }}{\bar w_2}(\vartheta) = - \infty $.
$li{m_{\vartheta \uparrow \hat \vartheta }}{\bar w_2}(\vartheta) = - \infty $. -
(iii)
 ${\bar \gamma _2}(\vartheta) \gt \pi (0) + h(\vartheta)$ if and only if
${\bar \gamma _2}(\vartheta) \gt \pi (0) + h(\vartheta)$ if and only if  $\vartheta \lt \hat \vartheta $.
$\vartheta \lt \hat \vartheta $.
Proposition 3, stated below, will imply Equation (22), if we let ![]() $s(\vartheta) = s\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right)$ and
$s(\vartheta) = s\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right)$ and ![]() $q(\vartheta) = q\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right)$.
$q(\vartheta) = q\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right)$.
(i) For any
 $\vartheta \lt \hat \vartheta $, there exists a unique number
$\vartheta \lt \hat \vartheta $, there exists a unique number  ${\gamma _2}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ such that for any
${\gamma _2}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ such that for any  $\gamma \in \left[ {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$, there are two unique and finite numbers
$\gamma \in \left[ {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$, there are two unique and finite numbers  $s( {\vartheta ,\gamma })$ and
$s( {\vartheta ,\gamma })$ and  $q( {\vartheta ,\gamma }),$ with
$q( {\vartheta ,\gamma }),$ with  $s( {\vartheta ,\gamma }) \le x_2^*( {\vartheta ,\gamma }) \le q( {\vartheta ,\gamma }) \lt \vartheta ,$ satisfying
$s( {\vartheta ,\gamma }) \le x_2^*( {\vartheta ,\gamma }) \le q( {\vartheta ,\gamma }) \lt \vartheta ,$ satisfying
 \begin{align*}w\!\left( {s( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = - k.\end{align*}
\begin{align*}w\!\left( {s( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = - k.\end{align*}
-
(ii) There exists a number
 $\bar \vartheta \in ( {0,\hat \vartheta })$ such that for any
$\bar \vartheta \in ( {0,\hat \vartheta })$ such that for any  $\vartheta \le \bar \vartheta $, there is a unique number
$\vartheta \le \bar \vartheta $, there is a unique number  $\gamma _2^*(\vartheta) \in \left[ {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ such that
(27)where
$\gamma _2^*(\vartheta) \in \left[ {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ such that
(27)where \begin{align}{f_2}\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right) = - K,\end{align}
is strictly decreasing in
\begin{align}{f_2}\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right) = - K,\end{align}
is strictly decreasing in \begin{align*}{f_2}( {\vartheta ,\gamma })\,:\!=\, \mathop \int \nolimits_{ - \infty }^\vartheta {\rm{min}}\!\left\{ {w( {x;\, \vartheta ,\gamma }) + k,0} \right\}{\rm{d}}x\end{align*}
\begin{align*}{f_2}( {\vartheta ,\gamma })\,:\!=\, \mathop \int \nolimits_{ - \infty }^\vartheta {\rm{min}}\!\left\{ {w( {x;\, \vartheta ,\gamma }) + k,0} \right\}{\rm{d}}x\end{align*}
 $\gamma $ on
$\gamma $ on  $\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$.
$\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$.
(iii)
 $\gamma _2^{\ast}(\vartheta)$ is continuous and strictly decreasing in
$\gamma _2^{\ast}(\vartheta)$ is continuous and strictly decreasing in  $\vartheta $ on
$\vartheta $ on  $\left( { - \infty ,\bar \vartheta } \right],$ with
$\left( { - \infty ,\bar \vartheta } \right],$ with  $\gamma _2^{\ast}\!\left( {\bar \vartheta } \right) = \pi (0) + h\!\left( {\bar \vartheta } \right)$.
$\gamma _2^{\ast}\!\left( {\bar \vartheta } \right) = \pi (0) + h\!\left( {\bar \vartheta } \right)$.
Proof. ![]() $(a)$ For any
$(a)$ For any ![]() $\vartheta \lt \hat \vartheta $, define
$\vartheta \lt \hat \vartheta $, define
which is well defined by Lemma 7![]() $(c)$. It follows from Proposition 1
$(c)$. It follows from Proposition 1![]() $(a)$ that
$(a)$ that
which, together with Lemma 3, implies that ![]() $w\big( {x_2^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big)$ is strictly decreasing in
$w\big( {x_2^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big)$ is strictly decreasing in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$. Furthermore, Proposition 1 also implies that
$\left( {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$. Furthermore, Proposition 1 also implies that ![]() ${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_2}(\vartheta)}}w\big( {x_2^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big) = - \infty $. Hence,
${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_2}(\vartheta)}}w\big( {x_2^{\ast}( {\vartheta ,\gamma });\,\vartheta ,\gamma } \big) = - \infty $. Hence, ![]() ${\gamma _2}(\vartheta)$ is well defined and finite.
${\gamma _2}(\vartheta)$ is well defined and finite.
Let ![]() ${\bar \vartheta _2}\,:\!=\, {\rm{supp}}\{ \vartheta \gt 0|{\bar w_2}(\vartheta) \ge - k\} $. By Lemma 7
${\bar \vartheta _2}\,:\!=\, {\rm{supp}}\{ \vartheta \gt 0|{\bar w_2}(\vartheta) \ge - k\} $. By Lemma 7![]() $(a)$, it is clear that
$(a)$, it is clear that ![]() ${\bar \vartheta _2} \gt 0$. If
${\bar \vartheta _2} \gt 0$. If ![]() $\vartheta \gt {\bar \vartheta _2}$, then we have
$\vartheta \gt {\bar \vartheta _2}$, then we have ![]() ${\gamma _2}(\vartheta) = \pi (0) + h( \vartheta),$ with
${\gamma _2}(\vartheta) = \pi (0) + h( \vartheta),$ with ![]() $w\!\left( {x_2^{\ast}( {\vartheta ,{\gamma _2}(\vartheta)});\,\vartheta ,{\gamma _2}(\vartheta)} \right) \lt - k$. If
$w\!\left( {x_2^{\ast}( {\vartheta ,{\gamma _2}(\vartheta)});\,\vartheta ,{\gamma _2}(\vartheta)} \right) \lt - k$. If ![]() $\vartheta \le {\bar \vartheta _2}$, then we have
$\vartheta \le {\bar \vartheta _2}$, then we have ![]() ${\gamma _2}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ and
${\gamma _2}(\vartheta) \in \left[ {\pi (0) + h( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ and ![]() $w\!\left( {x_2^{\ast}( {\vartheta ,{\gamma _2}(\vartheta)});\,\vartheta ,{\gamma _2}(\vartheta)} \right) = - k$. In either case, we have
$w\!\left( {x_2^{\ast}( {\vartheta ,{\gamma _2}(\vartheta)});\,\vartheta ,{\gamma _2}(\vartheta)} \right) = - k$. In either case, we have
For ![]() $\gamma \in \left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$, define
$\gamma \in \left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$, define
Then it follows from Proposition 1 and ![]() $w\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) = 0 \gt - k$ that both
$w\!\left( {\vartheta ;\,\vartheta ,\gamma } \right) = 0 \gt - k$ that both ![]() $s( {\vartheta ,\gamma })$ and
$s( {\vartheta ,\gamma })$ and ![]() $q( {\vartheta ,\gamma })$ are well defined, finite, and unique, and thus
$q( {\vartheta ,\gamma })$ are well defined, finite, and unique, and thus ![]() $s( {\vartheta ,\gamma }) \lt x_2^{\ast}( {\vartheta ,\gamma }) \lt q( {\vartheta ,\gamma }) \lt \vartheta $ and
$s( {\vartheta ,\gamma }) \lt x_2^{\ast}( {\vartheta ,\gamma }) \lt q( {\vartheta ,\gamma }) \lt \vartheta $ and ![]() $w\!\left( {s( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = - k$.
$w\!\left( {s( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = w\!\left( {q( {\vartheta ,\gamma });\,\vartheta ,\gamma } \right) = - k$.
![]() $\left( {{b}} \right)$ It follows from Proposition 1
$\left( {{b}} \right)$ It follows from Proposition 1![]() $(a)$ and the definitions of
$(a)$ and the definitions of ![]() $s( {\vartheta ,\gamma })$ and
$s( {\vartheta ,\gamma })$ and ![]() $q( {\vartheta ,\gamma })$ that
$q( {\vartheta ,\gamma })$ that
 \begin{align*}f_2(\vartheta,\gamma)= \left\{
\begin{array}{l@{\quad}l}
0 &\text {for $\gamma\in(\pi(0)+h(\vartheta), \gamma_2(\vartheta)]$},\\
\int_{s(\vartheta,\gamma)}^{q(\vartheta,\gamma)}[w(x;\, \vartheta,\gamma)+k]\, \mathrm{d}x
& \text{for $\gamma\in(\gamma_2(\vartheta),\bar{\gamma}_2(\vartheta))$},\\
-\infty & \text{for $\gamma\in[\bar{\gamma}_2(\vartheta),\infty)$}
\end{array}
\right.
\end{align*}
\begin{align*}f_2(\vartheta,\gamma)= \left\{
\begin{array}{l@{\quad}l}
0 &\text {for $\gamma\in(\pi(0)+h(\vartheta), \gamma_2(\vartheta)]$},\\
\int_{s(\vartheta,\gamma)}^{q(\vartheta,\gamma)}[w(x;\, \vartheta,\gamma)+k]\, \mathrm{d}x
& \text{for $\gamma\in(\gamma_2(\vartheta),\bar{\gamma}_2(\vartheta))$},\\
-\infty & \text{for $\gamma\in[\bar{\gamma}_2(\vartheta),\infty)$}
\end{array}
\right.
\end{align*}
for any ![]() $( {\vartheta ,\gamma })$ such that
$( {\vartheta ,\gamma })$ such that ![]() $\vartheta \lt \hat \vartheta $ and
$\vartheta \lt \hat \vartheta $ and ![]() $\gamma \gt \pi (0) + h(\vartheta)$.
$\gamma \gt \pi (0) + h(\vartheta)$.
Hence, by Lemma 3![]() $\left( {{b}} \right)$, we obtain that
$\left( {{b}} \right)$, we obtain that ![]() ${f_2}\!\left(\vartheta {,\gamma } \right)$ is strictly decreasing in
${f_2}\!\left(\vartheta {,\gamma } \right)$ is strictly decreasing in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$. Besides, we have
$\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$. Besides, we have ![]() ${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_2}(\vartheta)}}{f_2}( {\vartheta ,\gamma }) = - \infty $.
${\rm{li}}{{\rm{m}}_{\gamma \uparrow {{\bar \gamma }_2}(\vartheta)}}{f_2}( {\vartheta ,\gamma }) = - \infty $.
If ![]() $\vartheta \le {\bar \vartheta _2}$, then we have
$\vartheta \le {\bar \vartheta _2}$, then we have ![]() ${\rm{lim}}_{{\gamma \downarrow \gamma_2}(\vartheta)}{f_2}( {\vartheta ,\gamma }) = 0$. If
${\rm{lim}}_{{\gamma \downarrow \gamma_2}(\vartheta)}{f_2}( {\vartheta ,\gamma }) = 0$. If ![]() $\vartheta \in \!( {{{\bar \vartheta }_2},\hat \vartheta } )$, then
$\vartheta \in \!( {{{\bar \vartheta }_2},\hat \vartheta } )$, then ![]() ${\rm{li}}{{\rm{m}}_{\gamma \downarrow {\gamma _2}(\vartheta)}}{f_2}( {\vartheta ,\gamma }) = {f_2}\!\left( {\vartheta ,\pi (0) + h(\vartheta)} \right)$.
${\rm{li}}{{\rm{m}}_{\gamma \downarrow {\gamma _2}(\vartheta)}}{f_2}( {\vartheta ,\gamma }) = {f_2}\!\left( {\vartheta ,\pi (0) + h(\vartheta)} \right)$.
Define
(We can use a similar argument as that for ![]() $\underline{\vartheta}$ to obtain the well definedness of
$\underline{\vartheta}$ to obtain the well definedness of ![]() $\bar \vartheta $.) Clearly,
$\bar \vartheta $.) Clearly, ![]() $\bar \vartheta \gt 0$ since
$\bar \vartheta \gt 0$ since ![]() ${\bar \vartheta _2} \gt 0$. It follows from the continuity of
${\bar \vartheta _2} \gt 0$. It follows from the continuity of ![]() ${f_2}( {\vartheta ,\gamma })$ in
${f_2}( {\vartheta ,\gamma })$ in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ that the continuity of
$\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ that the continuity of ![]() ${f_2}( {\vartheta ,\gamma })$ can be implied by the continuity of
${f_2}( {\vartheta ,\gamma })$ can be implied by the continuity of ![]() $w( {x;\, \vartheta ,\gamma })$) and that for any
$w( {x;\, \vartheta ,\gamma })$) and that for any ![]() $\vartheta \le \bar \vartheta $, there exists a unique
$\vartheta \le \bar \vartheta $, there exists a unique ![]() $\gamma _2^{\ast}(\vartheta) \in \left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ such that
$\gamma _2^{\ast}(\vartheta) \in \left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$ such that ![]() ${f_2}\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right) = - K$.
${f_2}\!\left( {\vartheta ,\gamma _2^{\ast}(\vartheta)} \right) = - K$.
![]() $(c)$ By the definition of
$(c)$ By the definition of ![]() $\bar \vartheta $, we have
$\bar \vartheta $, we have ![]() $\gamma _2^{\ast}\!\left( {\bar \vartheta } \right) = \pi (0) + h\!\left( {\bar \vartheta } \right)$. That
$\gamma _2^{\ast}\!\left( {\bar \vartheta } \right) = \pi (0) + h\!\left( {\bar \vartheta } \right)$. That ![]() $\gamma _2^{\ast}(\vartheta)$ is continuous in
$\gamma _2^{\ast}(\vartheta)$ is continuous in ![]() $\vartheta $ follows from the monotonicity of
$\vartheta $ follows from the monotonicity of ![]() ${f_2}( {\vartheta ,\gamma })$ in
${f_2}( {\vartheta ,\gamma })$ in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$, the continuity of
$\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$, the continuity of ![]() ${f_2}( {\vartheta ,\gamma })$ in
${f_2}( {\vartheta ,\gamma })$ in ![]() $\vartheta $ and the implicit function theorem (see e.g. Theorem 1.1 in [Reference Kumagai24]). It remains to show that
$\vartheta $ and the implicit function theorem (see e.g. Theorem 1.1 in [Reference Kumagai24]). It remains to show that ![]() $\gamma _2^{\ast}(\vartheta)$ is strictly decreasing in
$\gamma _2^{\ast}(\vartheta)$ is strictly decreasing in ![]() $\vartheta $.
$\vartheta $.
Consider any ![]() ${\vartheta _1} \lt {\vartheta _2}$ on
${\vartheta _1} \lt {\vartheta _2}$ on ![]() $\left( { - \infty ,\bar \vartheta } \right]$. First we consider the case that
$\left( { - \infty ,\bar \vartheta } \right]$. First we consider the case that ![]() ${\vartheta _1} \in {\rm{\Theta }}\!\left( {\gamma _2^{\ast}( {{\vartheta _2}})} \right)$ or, equivalently,
${\vartheta _1} \in {\rm{\Theta }}\!\left( {\gamma _2^{\ast}( {{\vartheta _2}})} \right)$ or, equivalently, ![]() $\gamma _2^{\ast}( {{\vartheta _2}}) \gt \pi (0) + h\!\left( {{\vartheta _1}} \right)$. By Lemma 4
$\gamma _2^{\ast}( {{\vartheta _2}}) \gt \pi (0) + h\!\left( {{\vartheta _1}} \right)$. By Lemma 4![]() $\left( {{b}} \right)$, we have
$\left( {{b}} \right)$, we have ![]() $w\!\left( {x;\,{\vartheta _1},\gamma _2^{\ast}( {{\vartheta _2}})} \right) \gt w\!\left( {x;\,{\vartheta _2},\gamma _2^{\ast}( {{\vartheta _2}})} \right)$ for any
$w\!\left( {x;\,{\vartheta _1},\gamma _2^{\ast}( {{\vartheta _2}})} \right) \gt w\!\left( {x;\,{\vartheta _2},\gamma _2^{\ast}( {{\vartheta _2}})} \right)$ for any ![]() $x \le {\vartheta _1}$. Consequently, we have
$x \le {\vartheta _1}$. Consequently, we have
Hence, ![]() $\gamma _2^{\ast}\!\left( {{\vartheta _1}} \right) \gt \gamma _2^{\ast}( {{\vartheta _2}})$ by noting that
$\gamma _2^{\ast}\!\left( {{\vartheta _1}} \right) \gt \gamma _2^{\ast}( {{\vartheta _2}})$ by noting that ![]() ${f_2}( {\vartheta ,\gamma })$ is strictly decreasing in
${f_2}( {\vartheta ,\gamma })$ is strictly decreasing in ![]() $\gamma $ on
$\gamma $ on ![]() $\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$.
$\left( {{\gamma _2}( \vartheta),{{\bar \gamma }_2}(\vartheta)} \right)$.
For the case that ![]() $\gamma _2^{\ast}( {{\vartheta _2}}) \le \pi (0) + h\!\left( {{\vartheta _1}} \right)$, the result obviously holds as
$\gamma _2^{\ast}( {{\vartheta _2}}) \le \pi (0) + h\!\left( {{\vartheta _1}} \right)$, the result obviously holds as ![]() $\gamma _2^{\ast}\!\left( {{\vartheta _1}} \right) \gt \pi (0) + h\!\left( {{\vartheta _1}} \right)$.
$\gamma _2^{\ast}\!\left( {{\vartheta _1}} \right) \gt \pi (0) + h\!\left( {{\vartheta _1}} \right)$.
Proposition 4. There exists a unique number ![]() $\vartheta^{\star}\in [\underline{\vartheta}, \bar{\vartheta}]$ such that (23) holds.
$\vartheta^{\star}\in [\underline{\vartheta}, \bar{\vartheta}]$ such that (23) holds.
Proof. Let ![]() $\chi (\vartheta)\,:\!=\, \gamma _1^{\ast}(\vartheta) - \gamma _2^{\ast}(\vartheta)$. By Proposition 2
$\chi (\vartheta)\,:\!=\, \gamma _1^{\ast}(\vartheta) - \gamma _2^{\ast}(\vartheta)$. By Proposition 2![]() $(c)$ and Proposition 3
$(c)$ and Proposition 3![]() $(c)$, we have that
$(c)$, we have that ![]() $\chi(\vartheta)$ is continuous and strictly increasing in
$\chi(\vartheta)$ is continuous and strictly increasing in ![]() $\vartheta $ on
$\vartheta $ on ![]() $[ {\underline \vartheta ,\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } } ]$. In addition, we have
$[ {\underline \vartheta ,\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } } ]$. In addition, we have
where the second equality follows from Proposition 2![]() $(c)$ and the inequality uses the relation that
$(c)$ and the inequality uses the relation that ![]() $\gamma _2^{\ast}(\vartheta) \ge {\gamma _2}(\vartheta) \ge \pi (0) + h(\vartheta)$ according to Proposition 3
$\gamma _2^{\ast}(\vartheta) \ge {\gamma _2}(\vartheta) \ge \pi (0) + h(\vartheta)$ according to Proposition 3![]() $(a)$ and
$(a)$ and ![]() $\left( {{b}} \right)$. In a similar vein, we obtain
$\left( {{b}} \right)$. In a similar vein, we obtain ![]() $\chi \!\left( {\bar \vartheta } \right) \ge 0$. Therefore, there exists a unique
$\chi \!\left( {\bar \vartheta } \right) \ge 0$. Therefore, there exists a unique ![]() ${\vartheta ^{\ast}} \in \left[ {\underline \vartheta ,\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } } \right]$ such that
${\vartheta ^{\ast}} \in \left[ {\underline \vartheta ,\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over \vartheta } } \right]$ such that ![]() $\chi ( {{\vartheta ^{\ast}}}) = 0$.
$\chi ( {{\vartheta ^{\ast}}}) = 0$.
Proof of Theorem 1. ![]() $(a)$ Note that
$(a)$ Note that ![]() ${w^{\ast}}\!\left( \cdot \right)$ is a continuously differentiable solution to (6). Hence, Equations (20)–(22), together with Equation (23), ensure that Equations (6)–(10) are all satisfied. Besides, since
${w^{\ast}}\!\left( \cdot \right)$ is a continuously differentiable solution to (6). Hence, Equations (20)–(22), together with Equation (23), ensure that Equations (6)–(10) are all satisfied. Besides, since ![]() ${\gamma ^{\ast}} = \gamma _1^{\ast}( {{\vartheta ^{\ast}}}) \in \left( {\pi (0) + h( {{\vartheta ^{\ast}}}),{{\bar \gamma }_1}( {{\vartheta ^{\ast}}})} \right)$, Proposition 1 and the fact that
${\gamma ^{\ast}} = \gamma _1^{\ast}( {{\vartheta ^{\ast}}}) \in \left( {\pi (0) + h( {{\vartheta ^{\ast}}}),{{\bar \gamma }_1}( {{\vartheta ^{\ast}}})} \right)$, Proposition 1 and the fact that ![]() ${w^{\ast}}\!\left( {{q^{\ast}}} \right) = - k \lt l = {w^{\ast}}\!\left( {{Q^{\ast}}} \right)$ imply
${w^{\ast}}\!\left( {{q^{\ast}}} \right) = - k \lt l = {w^{\ast}}\!\left( {{Q^{\ast}}} \right)$ imply ![]() ${q^{\ast}} \lt {Q^{\ast}}$, which immediately concludes that
${q^{\ast}} \lt {Q^{\ast}}$, which immediately concludes that ![]() ${s^{\ast}} \lt {q^{\ast}} \lt {Q^{\ast}} \lt {S^{\ast}}$. The last assertion, that
${s^{\ast}} \lt {q^{\ast}} \lt {Q^{\ast}} \lt {S^{\ast}}$. The last assertion, that ![]() ${s^{\ast}} \lt 0 \lt {S^{\ast}}$, is obtained by noting that
${s^{\ast}} \lt 0 \lt {S^{\ast}}$, is obtained by noting that ![]() $x_1^{\ast} \gt 0 \gt x_2^{\ast}$, which follows from Proposition 1
$x_1^{\ast} \gt 0 \gt x_2^{\ast}$, which follows from Proposition 1![]() $\left( {\rm{d}} \right)$. The uniqueness of these parameters follows from the uniqueness of
$\left( {\rm{d}} \right)$. The uniqueness of these parameters follows from the uniqueness of ![]() ${\gamma ^{\ast}}$, as stated in Proposition 4.
${\gamma ^{\ast}}$, as stated in Proposition 4.
![]() $\left( {{b}} \right)$ It follows from Lemma 1 and Proposition 1
$\left( {{b}} \right)$ It follows from Lemma 1 and Proposition 1![]() $(a)$ that
$(a)$ that ![]() ${\mu ^{\ast}}(x) = \hat \mu \!\left( {{w^{\ast}}(x)} \right)$ is increasing in
${\mu ^{\ast}}(x) = \hat \mu \!\left( {{w^{\ast}}(x)} \right)$ is increasing in ![]() $x$ on
$x$ on ![]() $\left[ {{s^{\ast}},x_2^{\ast}} \right]$, decreasing in
$\left[ {{s^{\ast}},x_2^{\ast}} \right]$, decreasing in ![]() $x$ on
$x$ on ![]() $\left[ {x_2^{\ast},x_1^{\ast}} \right]$ and increasing in
$\left[ {x_2^{\ast},x_1^{\ast}} \right]$ and increasing in ![]() $x$ on
$x$ on ![]() $\left[ {x_1^{\ast},{S^{\ast}}} \right]$.
$\left[ {x_1^{\ast},{S^{\ast}}} \right]$.
4. Optimality of the Two-Sided Control Band Policy
The goal of this section is to show Theorem 2, which demonstrates the optimality of the policy ![]() ${\phi ^{\ast}}\,:\!=\, \!\left\{ {\!\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right),\!\left\{ {{\mu ^{\ast}}(x)\,:\,x \in [ {{s^{\ast}},{S^{\ast}}}]} \right\}} \right\}$. Recall that all the parameters in the policy
${\phi ^{\ast}}\,:\!=\, \!\left\{ {\!\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right),\!\left\{ {{\mu ^{\ast}}(x)\,:\,x \in [ {{s^{\ast}},{S^{\ast}}}]} \right\}} \right\}$. Recall that all the parameters in the policy ![]() ${\phi ^{\ast}}$ are specified by Theorem 1.
${\phi ^{\ast}}$ are specified by Theorem 1.
Theorem 2. The policy ![]() ${\phi ^*}$ is an optimal policy among all admissible policies, with
${\phi ^*}$ is an optimal policy among all admissible policies, with ![]() ${\gamma ^*}$ being the corresponding optimal long-run average cost.
${\gamma ^*}$ being the corresponding optimal long-run average cost.
The proof of Theorem 2 is based on the lower-bound approach, which is extensively used in the optimal control literature; see e.g. [Reference Ata, Harrison and Shepp2, Reference Dai and Yao10]. First, in Proposition 5, we present a lower-bound result, which provides a lower bound for the long-run average cost under any admissible policy if one can find a function that satisfies certain conditions. Next we show that ![]() ${\gamma ^{\ast}}$ is such a lower bound by constructing a function with these conditions all satisfied. Therefore,
${\gamma ^{\ast}}$ is such a lower bound by constructing a function with these conditions all satisfied. Therefore, ![]() ${\phi ^{\ast}}$ is an optimal policy, once we show that the long-run average cost under
${\phi ^{\ast}}$ is an optimal policy, once we show that the long-run average cost under ![]() ${\phi ^{\ast}}$ is exactly
${\phi ^{\ast}}$ is exactly ![]() ${\gamma ^{\ast}}$. This is established by Proposition 6.
${\gamma ^{\ast}}$. This is established by Proposition 6.
The following lower-bound result is established by the application of Itô’s formula.
Proposition 5. Suppose that there exists a constant ![]() $\gamma $ and a bound function
$\gamma $ and a bound function ![]() $f({\cdot}),$ with absolutely continuous and bounded derivative
$f({\cdot}),$ with absolutely continuous and bounded derivative ![]() $f'$ on
$f'$ on ![]() $\mathbb{R}$, and continuous second derivative
$\mathbb{R}$, and continuous second derivative ![]() $f''$ at all but a finite number of points, satisfying
$f''$ at all but a finite number of points, satisfying
and
Then we have ![]() $\texttt{AC}\!\left( {x,\phi } \right) \ge \gamma $ for any admissible policy
$\texttt{AC}\!\left( {x,\phi } \right) \ge \gamma $ for any admissible policy ![]() $\phi $ and initial state
$\phi $ and initial state ![]() $x$.
$x$.
Proof. It follows from Itô’s formula (see e.g. Proposition 1 in [Reference Ormeci, Dai and Vande Vate25]) that
 \begin{align} + \mathop \sum \limits_{i = 1}^2 {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^i} \!\left( {f\!\left( {{X_{\tau _n^i}}} \right) - f\!\left( {{X_{\tau _n^i - }}} \right)} \right)} \right].\end{align}
\begin{align} + \mathop \sum \limits_{i = 1}^2 {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^i} \!\left( {f\!\left( {{X_{\tau _n^i}}} \right) - f\!\left( {{X_{\tau _n^i - }}} \right)} \right)} \right].\end{align}
Notice that Equation (30) implies that
for all ![]() $x\in\mathbb{R}$ at which
$x\in\mathbb{R}$ at which ![]() $f''$ exists and
$f''$ exists and ![]() $\mu \in \mathcal{U}$. Furthermore, Equations (31) and (32) imply that for each
$\mu \in \mathcal{U}$. Furthermore, Equations (31) and (32) imply that for each ![]() $n \ge 0$, we have
$n \ge 0$, we have ![]() $f\!\left( {{X_{\tau _n^1}}} \right) - f\!\left( {{X_{\tau _n^1 - }}} \right) \ge - \!\left( {K + k\xi _n^1} \right)$ and
$f\!\left( {{X_{\tau _n^1}}} \right) - f\!\left( {{X_{\tau _n^1 - }}} \right) \ge - \!\left( {K + k\xi _n^1} \right)$ and ![]() $f\!\left( {{X_{\tau _n^2}}} \right) - f\!\left( {{X_{\tau _n^2 - }}} \right) \ge - \!\left( {L + \ell \xi _n^2} \right)$. Therefore, we have
$f\!\left( {{X_{\tau _n^2}}} \right) - f\!\left( {{X_{\tau _n^2 - }}} \right) \ge - \!\left( {L + \ell \xi _n^2} \right)$. Therefore, we have
 \begin{align*}&{\mathbb{E}_{x,\phi }}\!\left[ {f\!\left( {{X_t}} \right)} \right]\\[5pt]
&\ge {{\mathbb {E}}_{x,\phi }}\!\left[ {f\!\left( {{X_0}} \right)} \right] + {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {\gamma - c\!\left( {{\mu _s}} \right) - h\!\left( {{X_s}} \right)} \right){\rm{d}}s} \right] - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right)} \right]\\[5pt]
& \quad - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right]\\[5pt]
& = {{\mathbb {E}}_{x,\phi }}\!\left[ {f\!\left( {{X_0}} \right)} \right] + \gamma t - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {h\!\left( {{X_s}} \right) + c\!\left( {{\mu _s}} \right)} \right){\rm{d}}s + \mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right) + \mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right].\end{align*}
\begin{align*}&{\mathbb{E}_{x,\phi }}\!\left[ {f\!\left( {{X_t}} \right)} \right]\\[5pt]
&\ge {{\mathbb {E}}_{x,\phi }}\!\left[ {f\!\left( {{X_0}} \right)} \right] + {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {\gamma - c\!\left( {{\mu _s}} \right) - h\!\left( {{X_s}} \right)} \right){\rm{d}}s} \right] - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right)} \right]\\[5pt]
& \quad - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right]\\[5pt]
& = {{\mathbb {E}}_{x,\phi }}\!\left[ {f\!\left( {{X_0}} \right)} \right] + \gamma t - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {h\!\left( {{X_s}} \right) + c\!\left( {{\mu _s}} \right)} \right){\rm{d}}s + \mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right) + \mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right].\end{align*}
Dividing both sides of the inequality by ![]() $t$ and letting
$t$ and letting ![]() $t \to \infty $ gives
$t \to \infty $ gives
which further implies ![]() $\texttt{AC}\!\left( {x,\phi } \right) \ge \gamma $ by the boundedness of function
$\texttt{AC}\!\left( {x,\phi } \right) \ge \gamma $ by the boundedness of function ![]() $f$.
$f$.
It is worth mentioning that the proof of Proposition 11 in [Reference Cao and Yao7] contains an error, as (64) in that paper should take a different form. Consequently, the lower-bound result (62) there cannot be used to establish ![]() $\texttt{AC}\!\left( {x,\phi } \right) \ge \gamma $. In this paper, we show that this lower-bound result still holds, if additionally the function
$\texttt{AC}\!\left( {x,\phi } \right) \ge \gamma $. In this paper, we show that this lower-bound result still holds, if additionally the function ![]() $f$ is bounded.
$f$ is bounded.
We proceed to prove Theorem 2 by constructing a function such that the conditions in Proposition 5 are satisfied jointly with ![]() ${\gamma ^{\ast}}$. Due to the boundedness requirement for the function, the conventional construction, e.g. (3.6)–(3.8) in [Reference Jack and Zervos20], fails to work.
${\gamma ^{\ast}}$. Due to the boundedness requirement for the function, the conventional construction, e.g. (3.6)–(3.8) in [Reference Jack and Zervos20], fails to work.
The construction of such a function follows a similar procedure as that in the proof of Proposition 8 in [Reference Ata and Olsen4]. However, as there is no impulse control in their model, our construction is more involved.
Define
 \begin{align*}g(x)\,:\!=\, \!\left\{ {\begin{array}{l@{\quad}l}
{0,} & {x \in \left( { - \infty ,{s^{\ast}} - {\rm{\Delta }} - \delta } \right],}\\[5pt]
{ - \frac{{k\!\left( {x\; - {\rm{}}{s^{\ast}} + {\rm{\Delta }} + \delta } \right)}}{\delta },}& {x \in \left[ {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }}} \right],}\\[5pt]
{ - k,}& {x \in \left[ {{s^{\ast}} - {\rm{\Delta }},{s^{\ast}}} \right],}\\[5pt]
{{w^{\ast}}(x),}& {x \in [ {{s^{\ast}},{S^{\ast}}}],}\\[5pt]
{\ell ,}& {x \in \left[ {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}} \right],}\\[5pt]
{\frac{{\ell \!\left( {{S^{\ast}} + {\rm{\Delta }} + \delta \; - {\rm{}}x} \right)}}{\delta },}& {x \in \left[ {{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right],}\\[5pt]
{0,}& {x \in \left[ {{S^{\ast}} + {\rm{\Delta }} + \delta ,\infty } \right),}\end{array}} \right.\end{align*}
\begin{align*}g(x)\,:\!=\, \!\left\{ {\begin{array}{l@{\quad}l}
{0,} & {x \in \left( { - \infty ,{s^{\ast}} - {\rm{\Delta }} - \delta } \right],}\\[5pt]
{ - \frac{{k\!\left( {x\; - {\rm{}}{s^{\ast}} + {\rm{\Delta }} + \delta } \right)}}{\delta },}& {x \in \left[ {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }}} \right],}\\[5pt]
{ - k,}& {x \in \left[ {{s^{\ast}} - {\rm{\Delta }},{s^{\ast}}} \right],}\\[5pt]
{{w^{\ast}}(x),}& {x \in [ {{s^{\ast}},{S^{\ast}}}],}\\[5pt]
{\ell ,}& {x \in \left[ {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}} \right],}\\[5pt]
{\frac{{\ell \!\left( {{S^{\ast}} + {\rm{\Delta }} + \delta \; - {\rm{}}x} \right)}}{\delta },}& {x \in \left[ {{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right],}\\[5pt]
{0,}& {x \in \left[ {{S^{\ast}} + {\rm{\Delta }} + \delta ,\infty } \right),}\end{array}} \right.\end{align*}
where ![]() ${\rm{\Delta }}$ and
${\rm{\Delta }}$ and ![]() $\delta $ are positive numbers whose values will be determined later. (As we will find out, the value of
$\delta $ are positive numbers whose values will be determined later. (As we will find out, the value of ![]() $\delta $ can be arbitrarily chosen.) Clearly,
$\delta $ can be arbitrarily chosen.) Clearly, ![]() $g$ is continuous on
$g$ is continuous on ![]() $\mathbb{R}$ and differentiable on
$\mathbb{R}$ and differentiable on ![]() $\mathbb{R}\backslash \!\left\{ {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right\}$. We further define
$\mathbb{R}\backslash \!\left\{ {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right\}$. We further define ![]() $\tilde f(x)\,:\!=\, \mathop \int \nolimits_{{s^{\ast}}}^x g\!\left( y \right){\rm{d}}y$.
$\tilde f(x)\,:\!=\, \mathop \int \nolimits_{{s^{\ast}}}^x g\!\left( y \right){\rm{d}}y$.
The following result states that ![]() $\tilde f$ is such a function, as desired.
$\tilde f$ is such a function, as desired.
Lemma 8. By appropriately choosing the constant ![]() $\Delta $, the pair
$\Delta $, the pair ![]() $\left( {\tilde f,{\gamma ^*}} \right)$ satisfies the conditions stated in Proposition 5.
$\left( {\tilde f,{\gamma ^*}} \right)$ satisfies the conditions stated in Proposition 5.
Proof. It follows from Equation (10) and the definition of ![]() $\tilde f$ that
$\tilde f$ that ![]() $\tilde f$ is absolutely continuous and bounded, has bounded derivative
$\tilde f$ is absolutely continuous and bounded, has bounded derivative ![]() $g$ on
$g$ on ![]() $\mathbb{R}$ and also has continuous second derivative at
$\mathbb{R}$ and also has continuous second derivative at ![]() $\mathbb{R}\backslash \!\left\{ {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right\}$. Hence, it remains to show that we can choose a
$\mathbb{R}\backslash \!\left\{ {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right\}$. Hence, it remains to show that we can choose a ![]() ${\rm{\Delta }}$ such that
${\rm{\Delta }}$ such that ![]() $\left( {\tilde f,{\gamma ^{\ast}}} \right)$ satisfies Equations (30)–(32).
$\left( {\tilde f,{\gamma ^{\ast}}} \right)$ satisfies Equations (30)–(32).
We start by checking Equation (30). It follows from Equation (6) and the definition of ![]() $\tilde f$ that Equation (30) holds for
$\tilde f$ that Equation (30) holds for ![]() $x \in [ {{s^{\ast}},{S^{\ast}}}]$. For
$x \in [ {{s^{\ast}},{S^{\ast}}}]$. For ![]() $x \in ( {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}})$, we have
$x \in ( {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}})$, we have
 \begin{align*}& \frac{1}{2}{\sigma ^2}\tilde f''(x) + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \tilde f'(x) + c\!\left( \mu \right)} \right\} + h(x) = \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} + h(x)\\[5pt]
&\gt \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} + h\!\left( {{S^{\ast}}} \right) \gt \frac{1}{2}{\sigma ^2}\!\left( {{w^{\ast}}} \right)'\!\left( {{S^{\ast}}} \right) + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu {w^{\ast}}\!\left( {{S^{\ast}}} \right) + c\!\left( \mu \right)} \right\} + h\!\left( {{S^{\ast}}} \right) = {\gamma ^{\ast}},\end{align*}
\begin{align*}& \frac{1}{2}{\sigma ^2}\tilde f''(x) + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \tilde f'(x) + c\!\left( \mu \right)} \right\} + h(x) = \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} + h(x)\\[5pt]
&\gt \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} + h\!\left( {{S^{\ast}}} \right) \gt \frac{1}{2}{\sigma ^2}\!\left( {{w^{\ast}}} \right)'\!\left( {{S^{\ast}}} \right) + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu {w^{\ast}}\!\left( {{S^{\ast}}} \right) + c\!\left( \mu \right)} \right\} + h\!\left( {{S^{\ast}}} \right) = {\gamma ^{\ast}},\end{align*}
where the first equality follows from ![]() $\big( {{{\tilde f}^{\ast}}} \big)'(x) = \ell $ and
$\big( {{{\tilde f}^{\ast}}} \big)'(x) = \ell $ and ![]() $\big( {{{\tilde f}^{\ast}}} \big)''(x) = 0$ for
$\big( {{{\tilde f}^{\ast}}} \big)''(x) = 0$ for ![]() $x \in ( {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}});$ the first inequality follows from Assumption 1 and
$x \in ( {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}});$ the first inequality follows from Assumption 1 and ![]() $x \gt {S^{\ast}} \gt 0;$ the second inequality follows from Equation (10) and the fact that
$x \gt {S^{\ast}} \gt 0;$ the second inequality follows from Equation (10) and the fact that ![]() ${w^{\ast}}(x)$ is strictly decreasing in
${w^{\ast}}(x)$ is strictly decreasing in ![]() $x$ at
$x$ at ![]() ${S^{\ast}}$ and the last equality follows from Equation (6) with
${S^{\ast}}$ and the last equality follows from Equation (6) with ![]() $x = {S^{\ast}}$.
$x = {S^{\ast}}$.
Now we choose ![]() ${\rm{\Delta }}$ so that
${\rm{\Delta }}$ so that
which is guaranteed by Assumption 1![]() $\left( {{b}} \right)$ that
$\left( {{b}} \right)$ that ![]() ${\rm{li}}{{\rm{m}}_{x \to \infty }}h(x) = \infty $. (Recall that the constant
${\rm{li}}{{\rm{m}}_{x \to \infty }}h(x) = \infty $. (Recall that the constant ![]() $M$ is defined in Lemma 1.)
$M$ is defined in Lemma 1.)
Then for ![]() $x \in \left( {{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right)$, we have
$x \in \left( {{S^{\ast}} + {\rm{\Delta }},{S^{\ast}} + {\rm{\Delta }} + \delta } \right)$, we have
 \begin{align*}&\frac{1}{2}{\sigma ^2}\tilde f''(x) + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \tilde f'(x) + c\!\left( \mu \right)} \right\} + h(x)\\[5pt]
&= - \frac{{{\sigma ^2}\ell }}{{2\delta }} + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \frac{{\ell \!\left( {{S^{\ast}} + {\rm{\Delta }} + \delta \; - {\rm{}}x} \right)}}{\delta } + c\!\left( \mu \right)} \right\} + h(x)\\[5pt]
& \ge - \frac{{{\sigma ^2}\ell }}{{2\delta }} + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} - M\ell + h(x)\\[5pt]
& \ge \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} + h\!\left( {{S^{\ast}}} \right)\\[5pt]
& \gt {\gamma ^{\ast}},\end{align*}
\begin{align*}&\frac{1}{2}{\sigma ^2}\tilde f''(x) + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \tilde f'(x) + c\!\left( \mu \right)} \right\} + h(x)\\[5pt]
&= - \frac{{{\sigma ^2}\ell }}{{2\delta }} + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \frac{{\ell \!\left( {{S^{\ast}} + {\rm{\Delta }} + \delta \; - {\rm{}}x} \right)}}{\delta } + c\!\left( \mu \right)} \right\} + h(x)\\[5pt]
& \ge - \frac{{{\sigma ^2}\ell }}{{2\delta }} + \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} - M\ell + h(x)\\[5pt]
& \ge \mathop {{\rm{min}}}\limits_{\mu \in \mathcal{U}} \!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} + h\!\left( {{S^{\ast}}} \right)\\[5pt]
& \gt {\gamma ^{\ast}},\end{align*}
where the first inequality follows from the crude relation that ![]() ${\rm{mi}}{{\rm{n}}_{\mu \in \mathcal{U}}}\!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} \ge {\rm{mi}}{{\rm{n}}_{\mu \in \mathcal{U}}}\!\left\{ {\mu \ell ' + c\!\left( \mu \right)} \right\} - M\!\left| {\ell - \ell '} \right|;$ the second inequality follows from Equation (35) and the last inequality follows from the same argument as for the case of
${\rm{mi}}{{\rm{n}}_{\mu \in \mathcal{U}}}\!\left\{ {\mu \ell + c\!\left( \mu \right)} \right\} \ge {\rm{mi}}{{\rm{n}}_{\mu \in \mathcal{U}}}\!\left\{ {\mu \ell ' + c\!\left( \mu \right)} \right\} - M\!\left| {\ell - \ell '} \right|;$ the second inequality follows from Equation (35) and the last inequality follows from the same argument as for the case of ![]() $x \in ( {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}})$.
$x \in ( {{S^{\ast}},{S^{\ast}} + {\rm{\Delta }}})$.
For ![]() $x \in \left( {{S^{\ast}} + {\rm{\Delta }} + \delta ,\infty } \right)$, by a similar argument we obtain
$x \in \left( {{S^{\ast}} + {\rm{\Delta }} + \delta ,\infty } \right)$, by a similar argument we obtain
The cases of ![]() $ \in \left( {{s^{\ast}} - {\rm{\Delta }},{s^{\ast}}} \right)$,
$ \in \left( {{s^{\ast}} - {\rm{\Delta }},{s^{\ast}}} \right)$, ![]() $x \in \left( {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }}} \right)$ and
$x \in \left( {{s^{\ast}} - {\rm{\Delta }} - \delta ,{s^{\ast}} - {\rm{\Delta }}} \right)$ and ![]() $x \in \left( { - \infty ,{s^{\ast}} - {\rm{\Delta }} - \delta } \right)$ can be treated similarly, as long as we choose
$x \in \left( { - \infty ,{s^{\ast}} - {\rm{\Delta }} - \delta } \right)$ can be treated similarly, as long as we choose ![]() ${\rm{\Delta }}$ such that
${\rm{\Delta }}$ such that
which is guaranteed by Assumption 1![]() $\left( {{b}} \right)$ that
$\left( {{b}} \right)$ that ![]() ${\rm{li}}{{\rm{m}}_{x \to - \infty }}h(x) = \infty $.
${\rm{li}}{{\rm{m}}_{x \to - \infty }}h(x) = \infty $.
We next check (31). By the definition of ![]() $g$ as well as Propositions 1 and 3, we have that
$g$ as well as Propositions 1 and 3, we have that
 \begin{align*}g(x)\!\left\{ {\begin{array}{l@{\quad}l}{ = {w^{\ast}}(x) \lt - k,} & {x \in ( {{s^{\ast}},{q^{\ast}}}),}\\[5pt]
{ \ge - k,} & {x \notin ( {{s^{\ast}},{q^{\ast}}}).}\end{array}} \right.\end{align*}
\begin{align*}g(x)\!\left\{ {\begin{array}{l@{\quad}l}{ = {w^{\ast}}(x) \lt - k,} & {x \in ( {{s^{\ast}},{q^{\ast}}}),}\\[5pt]
{ \ge - k,} & {x \notin ( {{s^{\ast}},{q^{\ast}}}).}\end{array}} \right.\end{align*}
Therefore, for any ![]() $x \lt y$, we have
$x \lt y$, we have
where the last equality follows from Equation (7).
Finally, we check that Equation (32) holds for all ![]() $y \lt x$. Using
$y \lt x$. Using
we obtain
where the last equality follows from Equation (8).
Applying Lemma 8 to Proposition 5, we immediately obtain that ![]() ${\gamma ^{\ast}}$ is a lower bound for any admissible policy. By Theorem 1
${\gamma ^{\ast}}$ is a lower bound for any admissible policy. By Theorem 1![]() $(a)$, we are able to apply the following result with
$(a)$, we are able to apply the following result with ![]() $\left( {\phi ,V,\gamma } \right)$ being
$\left( {\phi ,V,\gamma } \right)$ being ![]() $\left( {{\phi ^{\ast}},{f^{\ast}},{\gamma ^{\ast}}} \right)$ to obtain that the long-run average cost under
$\left( {{\phi ^{\ast}},{f^{\ast}},{\gamma ^{\ast}}} \right)$ to obtain that the long-run average cost under ![]() ${\phi ^{\ast}}$ is exactly
${\phi ^{\ast}}$ is exactly ![]() ${\gamma ^{\ast}}$. This concludes the proof of Theorem 2.
${\gamma ^{\ast}}$. This concludes the proof of Theorem 2.
Proposition 6. Consider a policy ![]() $\phi = \left\{ {\left( {s,q,Q,S} \right),\!\left\{ {\mu (x) \in \mathcal{U}\,:\,x \in \left[ {s,S} \right]} \right\}} \right\},$ with
$\phi = \left\{ {\left( {s,q,Q,S} \right),\!\left\{ {\mu (x) \in \mathcal{U}\,:\,x \in \left[ {s,S} \right]} \right\}} \right\},$ with ![]() $s \lt q \le Q \lt S$. Suppose that there exist a constant
$s \lt q \le Q \lt S$. Suppose that there exist a constant ![]() $\gamma $ and a twice continuously differentiable function
$\gamma $ and a twice continuously differentiable function ![]() $V\,:\,\; [s, S]\to\mathbb{R}$ satisfying
$V\,:\,\; [s, S]\to\mathbb{R}$ satisfying
as well as
Then the average cost ![]() $\texttt{AC}\!\left( {x,\phi } \right)$ is
$\texttt{AC}\!\left( {x,\phi } \right)$ is ![]() $\gamma $ for any initial state
$\gamma $ for any initial state ![]() $x$.
$x$.
Proof. If the initial state ![]() $x \notin \!\left[ {s,S} \right]$, there will be a one-time control to bring it to
$x \notin \!\left[ {s,S} \right]$, there will be a one-time control to bring it to ![]() $q$ or
$q$ or ![]() $Q,$ and thus the state will stay in
$Q,$ and thus the state will stay in ![]() $\left[ {s,S} \right]$ forever under policy
$\left[ {s,S} \right]$ forever under policy ![]() $\phi $. The one-time finite control cost can be ignored in the long-run average cost, and thus it suffices to consider the case that the initial state
$\phi $. The one-time finite control cost can be ignored in the long-run average cost, and thus it suffices to consider the case that the initial state ![]() $x \in \left[ {s,S} \right]$.
$x \in \left[ {s,S} \right]$.
Since ![]() $V$ is twice continuously differentiable on
$V$ is twice continuously differentiable on ![]() $[ {s,S} ]$, it has a bounded derivative on
$[ {s,S} ]$, it has a bounded derivative on ![]() $[ {s,S} ]$. Furthermore, it follows from Equations (38) and (39) that under policy
$[ {s,S} ]$. Furthermore, it follows from Equations (38) and (39) that under policy ![]() $\phi $,
$\phi $, ![]() $V( {{X_{\tau _n^1}}} ) - V( {{X_{\tau _n^1 - }}} ) = - ( {K + k\xi _n^1} )$ and
$V( {{X_{\tau _n^1}}} ) - V( {{X_{\tau _n^1 - }}} ) = - ( {K + k\xi _n^1} )$ and ![]() $V( {{X_{\tau _n^2}}} ) - V( {{X_{\tau _n^2 - }}} ) = - ( {L + \ell \xi _n^2} )$. Since
$V( {{X_{\tau _n^2}}} ) - V( {{X_{\tau _n^2 - }}} ) = - ( {L + \ell \xi _n^2} )$. Since ![]() $s \le {X_t} \le S$ for all
$s \le {X_t} \le S$ for all ![]() $t \ge 0$ under policy
$t \ge 0$ under policy ![]() $\phi $, it follows from Equations (33) and (37) that
$\phi $, it follows from Equations (33) and (37) that
 \begin{align}&{{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_t}} \right)} \right]\nonumber\\[5pt]
&= {{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_0}} \right)} \right] + {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {\frac{1}{2}{\sigma ^2}V''\!\left( {{X_s}} \right) + \mu \!\left( {{X_s}} \right)V\!\left( {{X_s}} \right)} \right){\rm{d}}s} \right]\nonumber\\[5pt]
&+ \mathop \sum \limits_{i = 1}^2 {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^i} \!\left( {V\!\left( {{X_{\tau _n^i}}} \right) - V\!\left( {{X_{\tau _n^i - }}} \right)} \right)} \right]\nonumber\\[5pt]
& = {{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_0}} \right)} \right] + {{\mathbb {E}}_{\phi ,x}}\!\left[ {\mathop \int \nolimits_0^t \!\left( {\gamma - c\!\left( {\mu \!\left( {{X_s}} \right)} \right) - h\!\left( {{X_s}} \right)} \right){\rm{d}}s} \right]\nonumber\\[5pt]
& - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right)\!\left] { - {{\mathbb {E}}_{x,\phi }}} \right[\mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right]\nonumber\\[5pt]
& = {{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_0}} \right)} \right] + \gamma t\nonumber\\[5pt]
& - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {h\!\left( {{X_s}} \right) + c\!\left( {\mu \!\left( {{X_s}} \right)} \right)} \right){\rm{d}}s + \mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right) + \mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right].\end{align}
\begin{align}&{{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_t}} \right)} \right]\nonumber\\[5pt]
&= {{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_0}} \right)} \right] + {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {\frac{1}{2}{\sigma ^2}V''\!\left( {{X_s}} \right) + \mu \!\left( {{X_s}} \right)V\!\left( {{X_s}} \right)} \right){\rm{d}}s} \right]\nonumber\\[5pt]
&+ \mathop \sum \limits_{i = 1}^2 {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^i} \!\left( {V\!\left( {{X_{\tau _n^i}}} \right) - V\!\left( {{X_{\tau _n^i - }}} \right)} \right)} \right]\nonumber\\[5pt]
& = {{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_0}} \right)} \right] + {{\mathbb {E}}_{\phi ,x}}\!\left[ {\mathop \int \nolimits_0^t \!\left( {\gamma - c\!\left( {\mu \!\left( {{X_s}} \right)} \right) - h\!\left( {{X_s}} \right)} \right){\rm{d}}s} \right]\nonumber\\[5pt]
& - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right)\!\left] { - {{\mathbb {E}}_{x,\phi }}} \right[\mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right]\nonumber\\[5pt]
& = {{\mathbb {E}}_{x,\phi }}\!\left[ {V\!\left( {{X_0}} \right)} \right] + \gamma t\nonumber\\[5pt]
& - {{\mathbb {E}}_{x,\phi }}\!\left[ {\mathop \int \nolimits_0^t \!\left( {h\!\left( {{X_s}} \right) + c\!\left( {\mu \!\left( {{X_s}} \right)} \right)} \right){\rm{d}}s + \mathop \sum \limits_{n = 1}^{N_t^1} \!\left( {K + k\xi _n^1} \right) + \mathop \sum \limits_{n = 1}^{N_t^2} \!\left( {L + \ell \xi _n^2} \right)} \right].\end{align}
Note that ![]() ${\rm{mi}}{{\rm{n}}_{s \le x \le S}}V(x) \le V\!\left( {{X_t}} \right) \le {\rm{ma}}{{\rm{x}}_{s \le x \le S}}V(x)$, which implies
${\rm{mi}}{{\rm{n}}_{s \le x \le S}}V(x) \le V\!\left( {{X_t}} \right) \le {\rm{ma}}{{\rm{x}}_{s \le x \le S}}V(x)$, which implies ![]() ${\rm{li}}{{\rm{m}}_{t \to \infty }}{\mathbb{E}_{x,\phi }}\!\left[ {V\!\left( {{X_t}} \right)} \right]/$
${\rm{li}}{{\rm{m}}_{t \to \infty }}{\mathbb{E}_{x,\phi }}\!\left[ {V\!\left( {{X_t}} \right)} \right]/$ ![]() $t = 0$. Dividing both sides of Equation (40) by
$t = 0$. Dividing both sides of Equation (40) by ![]() $t$ and letting
$t$ and letting ![]() $t \to \infty $, we obtain
$t \to \infty $, we obtain ![]() $\texttt{AC}\!\left( {x,\phi } \right) = \gamma $.
$\texttt{AC}\!\left( {x,\phi } \right) = \gamma $.
5. Numerical Studies
According to Equation (3), it is clear that the long-run average cost under any policy ![]() $\phi $ is increasing in
$\phi $ is increasing in ![]() $K$,
$K$, ![]() $k$,
$k$, ![]() $L$, and
$L$, and ![]() $\ell $. Consequently, the optimal long-run average cost
$\ell $. Consequently, the optimal long-run average cost ![]() ${\gamma ^{\ast}}$ is also increasing in these values. However, it is unclear how the optimal policy parameters
${\gamma ^{\ast}}$ is also increasing in these values. However, it is unclear how the optimal policy parameters ![]() $\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ will vary with these values. Besides, it is interesting to investigate the value of joint drift rate and impulse control. That is, how much cost can be saved compared with the settings that only the drift rate control and the impulse control are allowed. In this section, we will conduct a series of numerical studies to answer these questions. The algorithms used for our numerical study are relegated to Appendix B.
$\left( {{s^{\ast}},{q^{\ast}},{Q^{\ast}},{S^{\ast}}} \right)$ will vary with these values. Besides, it is interesting to investigate the value of joint drift rate and impulse control. That is, how much cost can be saved compared with the settings that only the drift rate control and the impulse control are allowed. In this section, we will conduct a series of numerical studies to answer these questions. The algorithms used for our numerical study are relegated to Appendix B.
5.1. Impact of Cost Parameters
In the baseline model, we set the allowable drift rate ![]() $\mathcal{U}$ to be
$\mathcal{U}$ to be ![]() $\left[ { - 1,{\rm{}}1} \right]$, the drift cost function
$\left[ { - 1,{\rm{}}1} \right]$, the drift cost function ![]() $c\!\left( \mu \right)$ to be
$c\!\left( \mu \right)$ to be ![]() $\mu $, holding cost
$\mu $, holding cost ![]() $h(x)$ to be
$h(x)$ to be ![]() $\left| x \right|$, the variance
$\left| x \right|$, the variance ![]() ${\sigma ^2}$ to be 1 and all impulse cost parameters, including
${\sigma ^2}$ to be 1 and all impulse cost parameters, including ![]() $k$,
$k$, ![]() $K$,
$K$, ![]() $\ell $ and
$\ell $ and ![]() $L$, to be 1. Next we will vary cost parameters to investigate their impact on optimal policy parameters.
$L$, to be 1. Next we will vary cost parameters to investigate their impact on optimal policy parameters.
Effect of Holding Cost. We adopt the parameter setting as in the baseline model, except that now the holding cost ![]() $h(x)$ is
$h(x)$ is ![]() $a{x^ + } + b{x^ - }$. Then we let one of
$a{x^ + } + b{x^ - }$. Then we let one of ![]() $a$ or
$a$ or ![]() $b$ vary from 0.2 to 2.1, respectively, with the other one being fixed at 1. The corresponding numerical results are displayed in Figure 4.
$b$ vary from 0.2 to 2.1, respectively, with the other one being fixed at 1. The corresponding numerical results are displayed in Figure 4.

Figure 4. Impact of Holding Cost on the Optimal Control Parameters
Panel ![]() $(a)$ of Figure 4 demonstrates that when
$(a)$ of Figure 4 demonstrates that when ![]() $a$ increases, the optimal policy parameters
$a$ increases, the optimal policy parameters ![]() ${S^{\ast}}$,
${S^{\ast}}$, ![]() ${Q^{\ast}}$,
${Q^{\ast}}$, ![]() ${q^{\ast}}$ and
${q^{\ast}}$ and ![]() ${s^{\ast}}$ are all decreasing, with
${s^{\ast}}$ are all decreasing, with ![]() ${S^{\ast}}$ and
${S^{\ast}}$ and ![]() ${Q^{\ast}}$ decreasing more rapidly than
${Q^{\ast}}$ decreasing more rapidly than ![]() ${q^{\ast}}$ and
${q^{\ast}}$ and ![]() ${s^{\ast}}$. This is because when the positive holding cost
${s^{\ast}}$. This is because when the positive holding cost ![]() $a$ is large, the system manager wishes to keep the system state at a low (positive) level to reduce the overall cost, which can be achieved by choosing small values of these policy parameters. However, panel
$a$ is large, the system manager wishes to keep the system state at a low (positive) level to reduce the overall cost, which can be achieved by choosing small values of these policy parameters. However, panel ![]() $\left( {{b}} \right)$ illustrates an opposite effect of the negative holding cost
$\left( {{b}} \right)$ illustrates an opposite effect of the negative holding cost ![]() $b$. This also makes sense because when the negative holding cost is large, the system manager has a motive to keep the system state away from a large negative value.
$b$. This also makes sense because when the negative holding cost is large, the system manager has a motive to keep the system state away from a large negative value.
Effect of Drift Control Cost. Now, in the baseline model, we let the drift cost function ![]() $c\!\left( \mu \right)$ take the form
$c\!\left( \mu \right)$ take the form ![]() $c\mu $ (resp.
$c\mu $ (resp. ![]() $c\!\left| \mu \right|$), with
$c\!\left| \mu \right|$), with ![]() $c$ varying from 0.2 to 4 (resp. from 0.2 to 2). The numerical results are displayed in Figure 5.
$c$ varying from 0.2 to 4 (resp. from 0.2 to 2). The numerical results are displayed in Figure 5.

Figure 5. Impact of Drift Control Cost on the Optimal Control Parameters
Observing from panel ![]() $( {{a}} )$ of Figure 5, we find that in the case of
$( {{a}} )$ of Figure 5, we find that in the case of ![]() $c( \mu ) = c\mu $,
$c( \mu ) = c\mu $, ![]() ${S^{\ast}}$,
${S^{\ast}}$, ![]() ${Q^{\ast}}$,
${Q^{\ast}}$, ![]() ${q^{\ast}}$ and
${q^{\ast}}$ and ![]() ${s^{\ast}}$ all increase to some constants as
${s^{\ast}}$ all increase to some constants as ![]() $c$ increases. This can be explained as follows: When the drift rate cost parameter
$c$ increases. This can be explained as follows: When the drift rate cost parameter ![]() $c$ is large, to reduce the drift rate cost, the system manager would like to set the drift rate to its minimum,
$c$ is large, to reduce the drift rate cost, the system manager would like to set the drift rate to its minimum, ![]() $ - 1$. As a result, the system state has a downward trend such that the state will take a relatively long time in states having small values. To reduce the system’s holding cost, the system manager will set large relocation parameters. The observation that all these policy parameters keep fixed in fact holds in general. In fact, we can show that in the case of
$ - 1$. As a result, the system state has a downward trend such that the state will take a relatively long time in states having small values. To reduce the system’s holding cost, the system manager will set large relocation parameters. The observation that all these policy parameters keep fixed in fact holds in general. In fact, we can show that in the case of ![]() $c( \mu ) = c\mu $, there exists a number
$c( \mu ) = c\mu $, there exists a number ![]() ${c^\dagger }$ such that if
${c^\dagger }$ such that if ![]() $c \ge {c^\dagger }$, then the optimal policy
$c \ge {c^\dagger }$, then the optimal policy ![]() ${\phi ^{\ast}}( c )$ satisfies
${\phi ^{\ast}}( c )$ satisfies ![]() ${\phi ^{\ast}}( c ) = {\phi ^{\ast}}( {{c^\dagger }} ),$ and the optimal long-run average cost
${\phi ^{\ast}}( c ) = {\phi ^{\ast}}( {{c^\dagger }} ),$ and the optimal long-run average cost ![]() ${\gamma ^{\ast}}( c )$ satisfies
${\gamma ^{\ast}}( c )$ satisfies ![]() ${\gamma ^{\ast}}( c ) = {\gamma ^{\ast}}( {{c^\dagger }} ) + ( {c - {c^\dagger }} )\underline \mu $. (Here we attach the parameter
${\gamma ^{\ast}}( c ) = {\gamma ^{\ast}}( {{c^\dagger }} ) + ( {c - {c^\dagger }} )\underline \mu $. (Here we attach the parameter ![]() $c$ to emphasize the dependence on
$c$ to emphasize the dependence on ![]() $c$. This can be proved by checking that these parameters satisfy the conditions stated in Theorem 1
$c$. This can be proved by checking that these parameters satisfy the conditions stated in Theorem 1![]() $( {{a}} )$.)
$( {{a}} )$.)
Panel ![]() $\left( {{b}} \right)$ of Figure 5 displays the effect of
$\left( {{b}} \right)$ of Figure 5 displays the effect of ![]() $c$ in the case of
$c$ in the case of ![]() $c\!\left( \mu \right) = c\!\left| \mu \right|$, which demonstrates that both
$c\!\left( \mu \right) = c\!\left| \mu \right|$, which demonstrates that both ![]() ${s^{\ast}}$ and
${s^{\ast}}$ and ![]() ${q^{\ast}}$ increase to some negative constants, while both
${q^{\ast}}$ increase to some negative constants, while both ![]() ${Q^{\ast}}$ and
${Q^{\ast}}$ and ![]() ${S^{\ast}}$ decrease to positive constants. This can be explained similarly, with the except that now the drift rate will be set to be 0 when the drift rate cost parameter
${S^{\ast}}$ decrease to positive constants. This can be explained similarly, with the except that now the drift rate will be set to be 0 when the drift rate cost parameter ![]() $c$ is large.
$c$ is large.
Effect of Impulse Control Cost. Now we investigate the effect of impulse control cost, which is captured by four parameters: ![]() $\ell $,
$\ell $, ![]() $L$,
$L$, ![]() $k$ and
$k$ and ![]() $K$. Panel
$K$. Panel ![]() $(a)$ of Figure 6 is obtained by letting
$(a)$ of Figure 6 is obtained by letting ![]() $\ell $ vary from 0.1 to 2, with all other model parameters being fixed as in the baseline model. We observe that both the optimal policy parameters
$\ell $ vary from 0.1 to 2, with all other model parameters being fixed as in the baseline model. We observe that both the optimal policy parameters ![]() ${S^{\ast}}$ and
${S^{\ast}}$ and ![]() ${Q^{\ast}}$ are increasing in
${Q^{\ast}}$ are increasing in ![]() $\ell $, while both
$\ell $, while both ![]() ${s^{\ast}}$ and
${s^{\ast}}$ and ![]() ${q^{\ast}}$ are nearly constant with respect to
${q^{\ast}}$ are nearly constant with respect to ![]() $\ell $. This can be explained as follows: Since we vary only the downward impulse control cost, it can be expected that the upward control parameters
$\ell $. This can be explained as follows: Since we vary only the downward impulse control cost, it can be expected that the upward control parameters ![]() ${s^{\ast}}$ and
${s^{\ast}}$ and ![]() ${q^{\ast}}$ will not vary much with
${q^{\ast}}$ will not vary much with ![]() $\ell $. Since the upward impulse control is costly, the system manager will set large
$\ell $. Since the upward impulse control is costly, the system manager will set large ![]() ${S^{\ast}}$ and
${S^{\ast}}$ and ![]() ${Q^{\ast}}$ to reduce the frequency of upward control.
${Q^{\ast}}$ to reduce the frequency of upward control.

Figure 6. Impact of Impulse Control Cost on the Optimal Control Parameters
Similarly, panel ![]() $\left( {{b}} \right)$ of Figure 6 demonstrates how the optimal policy parameters vary with the downward fixed cost
$\left( {{b}} \right)$ of Figure 6 demonstrates how the optimal policy parameters vary with the downward fixed cost ![]() $L$. We find that
$L$. We find that ![]() ${S^{\ast}}$ is increasing in
${S^{\ast}}$ is increasing in ![]() $L$, while
$L$, while ![]() ${s^{\ast}}$,
${s^{\ast}}$, ![]() ${q^{\ast}}$ and
${q^{\ast}}$ and ![]() ${Q^{\ast}}$ are all quite insensitive with
${Q^{\ast}}$ are all quite insensitive with ![]() $L$. To explain the interesting pattern of
$L$. To explain the interesting pattern of ![]() ${Q^{\ast}}$ with respect to
${Q^{\ast}}$ with respect to ![]() $L$, we note that when the upward fixed cost is rather large, the system manager would like to take a rather large size when he performs an upward relocation. That is,
$L$, we note that when the upward fixed cost is rather large, the system manager would like to take a rather large size when he performs an upward relocation. That is, ![]() ${S^{\ast}} - {Q^{\ast}}$ should be increasing in
${S^{\ast}} - {Q^{\ast}}$ should be increasing in ![]() $L$. Hence,
$L$. Hence, ![]() ${Q^{\ast}}$ may not be necessarily increasing in
${Q^{\ast}}$ may not be necessarily increasing in ![]() $L$, which is different from the case of varying downward variable cost.
$L$, which is different from the case of varying downward variable cost.
The effects of the upward impulse control costs ![]() $k$ and
$k$ and ![]() $K$ are illustrated in panels
$K$ are illustrated in panels ![]() $(c)$ and
$(c)$ and ![]() $\left( {{d}} \right)$, whose explanation is similar and thus omitted.
$\left( {{d}} \right)$, whose explanation is similar and thus omitted.
5.2. The Value of Drift Rate Control
In this subsection, we investigate the value of drift rate control by considering a model in which only the impulse control is allowed. We still use the baseline model parameter setting, except now the drift rate cannot be adjusted but is a fixed value ![]() $\mu $, which takes its value from
$\mu $, which takes its value from ![]() $\mathcal{U} = \left[ { - 1,{\rm{}}1} \right]$. Using similar algorithms as in Appendix B, we can numerically obtain the value of the system’s optimal average cost
$\mathcal{U} = \left[ { - 1,{\rm{}}1} \right]$. Using similar algorithms as in Appendix B, we can numerically obtain the value of the system’s optimal average cost ![]() $\gamma \!\left( \mu \right)$. Figure 7 demonstrates that compared with the setting that only the impulse control is allowed, joint drift rate and impulse control can even halve the average cost, which indicates that allowing drift rate control can significantly reduce the overall operational cost.
$\gamma \!\left( \mu \right)$. Figure 7 demonstrates that compared with the setting that only the impulse control is allowed, joint drift rate and impulse control can even halve the average cost, which indicates that allowing drift rate control can significantly reduce the overall operational cost.

Figure 7. The Optimal Average Cost Without Drift Rate Control
6. Conclusion
In this paper, we present an analysis procedure for the joint drift rate and two-sided impulse control for a Brownian system, which is quite general, as our analysis requires only that the corresponding ODE takes the form of (O). As noted in [Reference Sun and Zhu30], in the presence of model uncertainty, a stochastic differential game (SDG) will appear, where the Bellman equation is also of form (O), except that the maximum instead of the minimum should be used in the definition of ![]() $\pi \!\left( w \right)$. Hence, it can be expected that our analysis procedure also applies to the SDG driven by Brownian motion.
$\pi \!\left( w \right)$. Hence, it can be expected that our analysis procedure also applies to the SDG driven by Brownian motion.
It is worth mentioning that our work can also be extended to the case that the diffusion term ![]() $\sigma $ depends on the current state, which takes the form of a function
$\sigma $ depends on the current state, which takes the form of a function ![]() $\sigma \!\left( {{X_t}} \right)$. In that case, the diffusion term
$\sigma \!\left( {{X_t}} \right)$. In that case, the diffusion term ![]() $\sigma $ in the ODE (O) is replaced with the strictly positive function
$\sigma $ in the ODE (O) is replaced with the strictly positive function ![]() $\sigma (x)$. To ensure the solvability of the ODE, the integrability of
$\sigma (x)$. To ensure the solvability of the ODE, the integrability of ![]() $1/{\sigma ^2}(x)$ is required; that is, for any
$1/{\sigma ^2}(x)$ is required; that is, for any ![]() $a \lt b, \int_a^b1/\sigma^2(x) \, \mathrm{d}x$ is finite. (One sufficient condition is that
$a \lt b, \int_a^b1/\sigma^2(x) \, \mathrm{d}x$ is finite. (One sufficient condition is that ![]() $\sigma (x)$ is continuous.) Given this requirement, we can show that most of our results still hold, with
$\sigma (x)$ is continuous.) Given this requirement, we can show that most of our results still hold, with ![]() $\sigma $ replaced by
$\sigma $ replaced by ![]() $\sigma (x)$ in accordance. However, some properties in Proposition 1 no longer hold for general diffusion function
$\sigma (x)$ in accordance. However, some properties in Proposition 1 no longer hold for general diffusion function ![]() $\sigma (x)$, since the solution
$\sigma (x)$, since the solution ![]() $w( {x;\, \vartheta ,\gamma })$ of the ODE (O) may converge to a finite value as
$w( {x;\, \vartheta ,\gamma })$ of the ODE (O) may converge to a finite value as ![]() $x \to \pm \infty $. To make the conclusions correct, we will need a stronger condition for
$x \to \pm \infty $. To make the conclusions correct, we will need a stronger condition for ![]() $\sigma (x)$; e.g. there exists a constant
$\sigma (x)$; e.g. there exists a constant ![]() $c \gt 0$ such that
$c \gt 0$ such that ![]() ${\rm{limin}}{{\rm{f}}_{x \to \pm \infty }}h(x)/{\sigma ^2}(x) \gt c$.
${\rm{limin}}{{\rm{f}}_{x \to \pm \infty }}h(x)/{\sigma ^2}(x) \gt c$.
At the end of this paper, we list several topics that are worthy of consideration in future. First, singular control is also a well-known control type, but it is not studied in this paper. Singular control arises in situations such as customer admission in queueing systems and demand outsourcing in production systems. As found in [Reference He, Yao and Zhang18], there is a close connection between singular control and impulse control. In fact, impulse control in our model will take the form of Equations (9) and (10), with Equations (7) and (8) no longer needed. Hence, it is expected that our analysis procedure can still work in the presence of singular control.
Second, in this paper the system state is one-dimensional, while in many other settings it may be multi-dimensional. In this setting, the guess-and-verify method adopted in this paper may not work well, as now the guessed policy may take a complex structure, and the best policy parameters cannot be found easily. Of course, in some models motivated by queueing controls, the corresponding multi-dimensional diffusion control problem can be reduced to a one-dimensional problem, in which case our results still can apply (see e.g. [Reference Harrison and López16, Reference Rubino and Ata29]). However, in other models, it will not be so [Reference Ke, Shen and Villas-Boas22]. Even if the guess-and-verify method can still work in some simple cases, it will be more interesting to devise theoretical methods or efficient algorithms to analyze these models.
Third, the system state dynamics in this paper is rather simple, as it follows a Brownian motion. It will be interesting to consider the case in which the system state follows some other stochastic process, such as a Lévy process. Besides, the diffusion coefficient (![]() $\sigma $ in this paper) can also be controlled in some practical situations. In this setting, the ODE (6) will be changed, and thus its analysis will be different [Reference Yamazaki33]. In addition, it will also be practically relevant to take the time-varying feature into account when modelling the state dynamics.
$\sigma $ in this paper) can also be controlled in some practical situations. In this setting, the ODE (6) will be changed, and thus its analysis will be different [Reference Yamazaki33]. In addition, it will also be practically relevant to take the time-varying feature into account when modelling the state dynamics.
Finally, we can also consider other criterions such as the infinite discounted criterion, as some literature demonstrates that the optimal control policy may take a different form than that under the long-run average criterion, with the analysis also being different [Reference Xu, Yao and Zhang32].
Appendix A. A Heuristic Argument for Equations (6)–(10)
In this appendix, we explain why the optimal parameters should satisfy the ODE [Equation (6)] and free boundary conditions Equations (7)–(10). For a given policy ![]() $\phi = \left\{ {( {s,q,Q,S}),\!\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}} \right\}$, let
$\phi = \left\{ {( {s,q,Q,S}),\!\left\{ {\mu (x)\,:\,x \in \left[ {s,S} \right]} \right\}} \right\}$, let ![]() $V(x)$ be the relative value function, which is the difference between the expected cumulative cost from state
$V(x)$ be the relative value function, which is the difference between the expected cumulative cost from state ![]() $x\in\mathbb{R}$ to state
$x\in\mathbb{R}$ to state ![]() $0$ and the cost
$0$ and the cost ![]() $\gamma \tau \!\left( {x,0} \right)$, where
$\gamma \tau \!\left( {x,0} \right)$, where ![]() $\gamma $ is the long-run average cost under policy
$\gamma $ is the long-run average cost under policy ![]() $\phi $ and
$\phi $ and ![]() $\tau \!\left( {x,0} \right)$ is the first time when the system state hits
$\tau \!\left( {x,0} \right)$ is the first time when the system state hits ![]() $0$, starting from
$0$, starting from ![]() $x$.
$x$.
First, the definition of ![]() $V$ implies that
$V$ implies that ![]() $V$ should satisfy
$V$ should satisfy ![]() $V\!\left( s \right) = V\!\left( q \right) + K + k \cdot ( {q - s})$ and
$V\!\left( s \right) = V\!\left( q \right) + K + k \cdot ( {q - s})$ and ![]() $V\!\left( S \right) = V\!\left( Q \right) + L + \ell \cdot \left( {S - Q} \right)$, which yield Equations (7) and (8), respectively, by letting
$V\!\left( S \right) = V\!\left( Q \right) + L + \ell \cdot \left( {S - Q} \right)$, which yield Equations (7) and (8), respectively, by letting ![]() ${w^{\ast}}(x) = V'(x)$. Next, we show that
${w^{\ast}}(x) = V'(x)$. Next, we show that ![]() $V$ should satisfy Equations (6), (9), and (10) if
$V$ should satisfy Equations (6), (9), and (10) if ![]() $\phi $ is optimal. If
$\phi $ is optimal. If ![]() $\phi $ is optimal, by the principle of optimality, for
$\phi $ is optimal, by the principle of optimality, for ![]() ${X_0} = x \in \left( {s,S} \right)$ and a small time interval with length
${X_0} = x \in \left( {s,S} \right)$ and a small time interval with length ![]() $\delta $,
$\delta $, ![]() $V(x)$ should satisfy
$V(x)$ should satisfy
with ![]() ${X_u} = x + \mathop \int \nolimits_0^u {\mu _\upsilon }{\rm{d}}\upsilon + \sigma {B_u}$ for
${X_u} = x + \mathop \int \nolimits_0^u {\mu _\upsilon }{\rm{d}}\upsilon + \sigma {B_u}$ for ![]() $u \in \left[ {0,\delta } \right]$. It follows from a standard argument for the dynamic programming equation [see e.g. Equation 12] that
$u \in \left[ {0,\delta } \right]$. It follows from a standard argument for the dynamic programming equation [see e.g. Equation 12] that ![]() $V(x)$ satisfies
$V(x)$ satisfies
which implies Equation (6) by noting that ![]() ${w^{\ast}} = V'$. Furthermore, starting from state
${w^{\ast}} = V'$. Furthermore, starting from state ![]() $S$, if it is optimal to jump to state
$S$, if it is optimal to jump to state ![]() $Q$, then
$Q$, then ![]() $Q$ should be chosen to minimize
$Q$ should be chosen to minimize ![]() $V\!\left( Q \right) + L + \ell \cdot \left( {S - Q} \right)$. The first-order optimality condition gives
$V\!\left( Q \right) + L + \ell \cdot \left( {S - Q} \right)$. The first-order optimality condition gives ![]() $V'\!\left( Q \right) = \ell $, which is the first equality in Equation (10). Besides, for
$V'\!\left( Q \right) = \ell $, which is the first equality in Equation (10). Besides, for ![]() $x \ge S$, under policy
$x \ge S$, under policy ![]() $\phi $, we must have
$\phi $, we must have ![]() $V(x) = V\!\left( Q \right) + L + \ell \cdot \left( {x - Q} \right)$. By the smooth-pasting principle under the optimal policy, the left and right derivatives of
$V(x) = V\!\left( Q \right) + L + \ell \cdot \left( {x - Q} \right)$. By the smooth-pasting principle under the optimal policy, the left and right derivatives of ![]() $V$ at
$V$ at ![]() $S$ should be equal, which gives
$S$ should be equal, which gives ![]() $V'\!\left( S \right) = \ell $, the second equality in Equation (10). Finally, a similar analysis gives us Equation (9).
$V'\!\left( S \right) = \ell $, the second equality in Equation (10). Finally, a similar analysis gives us Equation (9).
Appendix B. Algorithms
The procedure described in Section 3.2 in fact gives us a set of algorithms (Algorithms 1–3) to find the optimal policy parameters. Algorithm 1 in Appendix B presents a computational procedure to obtain ![]() $\gamma _1^{\ast}(\vartheta)$ for any
$\gamma _1^{\ast}(\vartheta)$ for any ![]() $\vartheta $. Since
$\vartheta $. Since ![]() $\gamma _1^{\ast}(\vartheta) \ge \pi (0) + h(\vartheta)$, the lower bound for
$\gamma _1^{\ast}(\vartheta) \ge \pi (0) + h(\vartheta)$, the lower bound for ![]() $\gamma _1^{\ast}(\vartheta)$, denoted as
$\gamma _1^{\ast}(\vartheta)$, denoted as ![]() ${\gamma _l}$, can be initialized to
${\gamma _l}$, can be initialized to ![]() $\pi (0) + h(\vartheta)$. Then, we gradually increase a number
$\pi (0) + h(\vartheta)$. Then, we gradually increase a number ![]() ${\gamma _u}$, from
${\gamma _u}$, from ![]() $\pi (0) + h(\vartheta)$ until that
$\pi (0) + h(\vartheta)$ until that ![]() ${f_1}\!\left( {\vartheta ,{\gamma _u}} \right) \gt L$, which guarantees that
${f_1}\!\left( {\vartheta ,{\gamma _u}} \right) \gt L$, which guarantees that ![]() ${\gamma _u}$ is an upper bound for
${\gamma _u}$ is an upper bound for ![]() $\gamma _1^{\ast}(\vartheta)$ by Lemma 2
$\gamma _1^{\ast}(\vartheta)$ by Lemma 2![]() $\left( b \right)$ (lines 1–7). Given these bounds,
$\left( b \right)$ (lines 1–7). Given these bounds, ![]() $\gamma _1^{\ast}(\vartheta)$ is pinned down by a bisection procedure on
$\gamma _1^{\ast}(\vartheta)$ is pinned down by a bisection procedure on ![]() $\gamma $ (lines 9–16), which is also guaranteed by Lemma 2
$\gamma $ (lines 9–16), which is also guaranteed by Lemma 2![]() $\left( {{b}} \right)$.
$\left( {{b}} \right)$.
Similarly, Algorithm 2 presents a procedure to compute ![]() $\gamma _2^{\ast}(\vartheta)$, which is justified by Lemma 3
$\gamma _2^{\ast}(\vartheta)$, which is justified by Lemma 3![]() $\left( {{b}} \right)$. Finally, Algorithm 3 performs a bisection procedure on
$\left( {{b}} \right)$. Finally, Algorithm 3 performs a bisection procedure on ![]() $\vartheta $ to obtain
$\vartheta $ to obtain ![]() ${\vartheta ^{\ast}}$, which is guaranteed by Lemma 2
${\vartheta ^{\ast}}$, which is guaranteed by Lemma 2![]() $(c)$, Lemma 3
$(c)$, Lemma 3![]() $(c)$ and Proposition 4. All other policy parameters are then immediately determined using the expressions displayed after Equation (23).
$(c)$ and Proposition 4. All other policy parameters are then immediately determined using the expressions displayed after Equation (23).
It is worth pointing out that when conducting these algorithms, we need to solve problem (O) for each ![]() $( {\vartheta ,\gamma })$. Fortunately, this problem can be readily solved by any commercial solver such as Matlab.
$( {\vartheta ,\gamma })$. Fortunately, this problem can be readily solved by any commercial solver such as Matlab.
Algorithm 1 Binary-search Routine to Find ![]() $\gamma _1^ \star (\vartheta )$
$\gamma _1^ \star (\vartheta )$

Algorithm 2 Binary-search Routine to Find ![]() $\gamma _2^ \star (\vartheta )$
$\gamma _2^ \star (\vartheta )$

Algorithm 3 Binary-search Routine to Find ![]() ${\vartheta ^ \star }$
${\vartheta ^ \star }$

Acknowledgements
We are grateful to the editors and two anonymous referees for their thoughtful and constructive comments. In addition, we thank one referee for bringing the closely related work [Reference Jack and Zervos20] to our attention.
Funding information
P. Cao is supported in part by the National Natural Science Foundation of China (Grant No. 72122019). D. Yao is supported in part by the National Key R&D Program of China (Grant Nos. 2021YFA1000300 and 2021YFA1000301), the CAS Project for Young Scientists in Basic Research (Grant No. YSBR-008) and the National Natural Science Foundation of China (Grant No. 12371325).
Competing interests
There were no competing interests that arose during the preparation or publication process of this article to declare.