Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T08:09:48.711Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of segregating sites for populations with large family sizes

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  01 July 2016

M Möhle
M Möhle*
Affiliation:
Eberhard Karls Universität Tübingen
*
∗ Postal address: Mathematisches Institut der Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present recursions for the total number, Sn, of mutations in a sample of n individuals, when the underlying genealogical tree of the sample is modelled by a coalescent process with mutation rate r>0. The coalescent is allowed to have simultaneous multiple collisions of ancestral lineages, which corresponds to the existence of large families in the underlying population model. For the subclass of Λ-coalescent processes allowing for multiple collisions, such that the measure Λ(dx)/x is finite, we prove that Sn/(nr) converges in distribution to a limiting variable, S, characterized via an exponential integral of a certain subordinator. 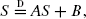When the measure Λ(dx)/x2 is finite, the distribution of S coincides with the stationary distribution of an autoregressive process of order 1 and is uniquely determined via a stochastic fixed-point equation of the form with specific independent random coefficients A and B. Examples are presented in which explicit representations for (the density of) S are available. We conjecture that Sn/E(Sn)→1 in probability if the measure Λ(dx)/x is infinite.

Keywords

Autoregressive processcoalescent processinfinitely-many-sites modelmultiple collisionssegregating sitesstochastic difference equationtotal number of mutations

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces 92D10: Genetics
Secondary: 60F05: Central limit and other weak theorems 92D15: Problems related to evolution
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 38 , Issue 3 , September 2006 , pp. 750 - 767
Copyright
Copyright © Applied Probability Trust 2006 

References

Berestycki, J., Berestycki, N. and Schweinsberg, J. (2005). Small-time behavior of beta-coalescents. Preprint.Google Scholar
Berestycki, J., Berestycki, N. and Schweinsberg, J. (2006). Beta-coalescents and continuous stable random trees. Preprint.Google Scholar
Bertoin, J. and Le Gall, J.-F. (2003). Stochastic flows associated to coalescent processes. Prob. Theory Relat. Fields 126, 261–288.Google Scholar
Bertoin, J. and Yor, M. (2001). On subordinators, self-similar Markov processes and some factorizations of the exponential variable. Electron. Commun. Prob. 6, 95–106.CrossRefGoogle Scholar
Bolthausen, E. and Sznitman, A.-S. (1998). On Ruelle's probability cascades and an abstract cavity method. Commun. Math. Phys. 197, 247–276.Google Scholar
Brandt, A. (1986). The stochastic equation Y n 1=A n Y n B n with stationary coefficients. Adv. Appl. Prob. 18, 211–220.Google Scholar
Carmona, P., Petit, F. and Yor, M. (1997). On the distribution and asymptotic results for exponential functionals of Lévy processes. In Exponential Functionals and Principal Values Related to Brownian Motion, ed. Yor, M., Biblioteca de la Revista Matematica Iberoamericana, Madrid, pp. 73–121.Google Scholar
Durrett, R. and Schweinsberg, J. (2005). A coalescent model for the effect of advantageous mutations on the genealogy of a population. Stoch. Process. Appl. 115, 1628–1657.Google Scholar
Goldschmidt, C. and Martin, J. B. (2005). Random recursive trees and the Bolthausen–Sznitman coalescent. Electron. J. Prob. 10, 718–745.CrossRefGoogle Scholar
Gut, A. (2003). On the moment problem for random sums. J. Appl. Prob. 40, 797–802.CrossRefGoogle Scholar
Hedgecock, D. (1994). Does variance in reproductive success limit effective population sizes of marine organisms? In Genetics and Evolution of Aquatic Organisms, ed. Beaumont, A., Chapman and Hall, London, pp. 122–134.Google Scholar
Kingman, J. F. C. (1982). Exchangeability and the evolution of large populations. In Exchangeability in Probability and Statistics, eds Koch, G. and Spizzichino, F., North-Holland, Amsterdam, pp. 97–112.Google Scholar
Kingman, J. F. C. (1982). On the genealogy of large populations. In Essays in Statistical Science (J. Appl. Prob. Spec. Vol. 19A), eds Gani, J. and Hannan, E. J., Applied Probability Trust, Sheffield, pp. 27–43.Google Scholar
Kingman, J. F. C. (1982). The coalescent. Stoch. Process. Appl. 13, 235–248.CrossRefGoogle Scholar
Kingman, J. F. C. (2000). Origins of the coalescent: 1974–1982. Genetics 156, 1461–1463.Google Scholar
Möhle, M. and Sagitov, S. (2001). A classification of coalescent processes for haploid exchangeable population models. Ann. Prob. 29, 1547–1562.Google Scholar
Neininger, R. and Rüschendorf, L. (2004). On the contraction method with degenerate limit equation. Ann. Prob. 32, 2838–2856.CrossRefGoogle Scholar
Pitman, J. (1999). Coalescents with multiple collisions. Ann. Prob. 27, 1870–1902.Google Scholar
Rösler, U. (1991). A limit theorem for ‘Quicksort’. RAIRO Inf. Théoret. Appl. 25, 85–100.Google Scholar
Rösler, U. (1992). A fixed point theorem for distributions. Stoch. Process. Appl. 42, 195–214.Google Scholar
Rösler, U. and Rüschendorf, L. (2001). The contraction method for recursive algorithms. Algorithmica 29, 3–33.Google Scholar
Sagitov, S. (1999). The general coalescent with asynchronous mergers of ancestral lines. J. Appl. Prob. 36, 1116–1125.CrossRefGoogle Scholar
Schweinsberg, J. (2000). A necessary and sufficient condition for the Λ-coalescent to come down from infinity. Electron. Commun. Prob. 5, 1–11.CrossRefGoogle Scholar
Schweinsberg, J. (2000). Coalescents with simultaneous multiple collisions. Electron. J. Prob. 5, 1–50.Google Scholar
Tajima, F. (1989). Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123, 585–595.CrossRefGoogle ScholarPubMed
Vervaat, W. (1979). On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.Google Scholar
Watterson, G. A. (1975). On the number of segregating sites in genetical models without recombination. Theoret. Pop. Biol. 7, 256–276.Google Scholar