Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T07:45:30.616Z Has data issue: false hasContentIssue false
  • English
  • Français

On the fraction of random points by specified nearest-neighbour interrelations and degree of attraction

Published online by Cambridge University Press:  01 July 2016

Norbert Henze
Norbert Henze*
Affiliation:
University of Hannover
*
∗Postal address: Institut für Mathematische Stochastik, Universität Hannover, Welfengarten 1, D-3000 Hannover 1, W. Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

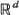Let Z1, …, Zn be i.i.d. random vectors (‘points') defined in having common density f(x) that is assumed to be continuous almost everywhere. For a fixed but otherwise arbitrary norm |.| on , consider the fraction Vn of those points Z1, …, Zn that are the lth nearest neighbour (with respect to |.|) to their own kth nearest neighbour, and write Sn for the fraction of points that are the nearest neighbour of exactly k other points. We derive the stochastic limits of Vn and Sn, as n tends to∞, and show how the results may be applied to the multivariate non-parametric two-sample problem.

Keywords

NEAREST NEIGHBOURSGEOMETRIC PROBABILITYPOISSON PROCESSMULTIVARIATE TWO-SAMPLE PROBLEM
Type
Research Article
Information
Advances in Applied Probability , Volume 19 , Issue 4 , December 1987 , pp. 873 - 895
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bickel, P. J. and Breiman, L. (1983) RK distances, moment bounds, limit theorems and a goodness of fit test. Ann. Prob. 11, 185–214.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Clark, P. J. (1955) Grouping in spatial distributions. Science 123, 373–374.Google Scholar
Clark, P. J. and Evans, F. C. (1955) On some aspects of spatial pattern in biological populations. Science 121, 397–398.Google Scholar
Cover, T. M. and Hart, P. E. (1967) Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 14, 21–27.Google Scholar
Cox, T. F. (1981) Reflexive nearest neighbours. Biometrics 37, 367–369.Google Scholar
Dacey, M. F. (1969) Proportion of reflexive nth order neighbors in spatial distribution. Geographical Analysis 1, 385–388.Google Scholar
Fritz, J. (1975) Distribution-free exponential error bound for nearest neighbor pattern classification. IEEE Trans. Inf. Theory 21, 552–557.Google Scholar
Hall, P. (1983) On near neighbour estimates of a multivariate density. J. Mult. Anal. 13, 24–39.Google Scholar
Henze, N. (1983) An asymptotic theorem on the maximum minimum distance of independent random vectors, with application to a goodness of fit test in ℝ P and on the sphere surface (in German). Metrika 30, 245–259.Google Scholar
Henze, N. (1984) On the number of random points with nearest neighbour of the same type and a multivariate two-sample test (in German). Metrika 31, 259–273.Google Scholar
Henze, N. (1985) A multivariate two- and multisample test based on the number of nearest neighbour type coincidences (in German). Habilitationsschrift, University of Hannover.Google Scholar
Henze, N. (1986a) On the probability that a random point is the jth nearest neighbour to its own kth nearest neighbour. J. Appl. Prob. 23, 221–226.Google Scholar
Henze, N. (1986b) On the fraction of random points that are the nearest neighbour of exactly k other points. 2nd Catalan Int. Symp. Statist. 2, 145–148.Google Scholar
Henze, N. (1986C) A multivariate two-sample test based on the number of nearest neighbor type coincidences. Ann. Statist.Google Scholar
Mack, Y. P. and Rosenblatt, M. (1979) Multivariate k nearest neighbor density estimates. J. Mult. Anal. 9, 1–15.Google Scholar
Maloney, L. T. (1983) Nearest neighbor analysis of point processes: Simulations and evaluations. J. Math. Psychol. 27, 251–260.Google Scholar
Miles, R. E. (1974) A synopsis of ‘Poisson flats in Euclidean spaces’. In Stochastic Geometry, ed. Harding, E. F. and Kendall, D. G.. Wiley, London, 202–227.Google Scholar
Moore, D. S. and Yackel, J. W. (1977) Consistency properties of nearest-neighbor density estimates. Ann. Statist. 5, 143–154.Google Scholar
Newman, C. M. and Rinott, Y. (1985) Nearest neighbors and Voronoi regions in high-dimensional point processes with various distance functions. Adv. Appl. Prob. 17, 794–809.Google Scholar
Newman, C. M., Rinott, Y. and Tversky, A. (1983) Nearest neighbors and Voronoi regions in certain point processes. Adv. Appl. Prob. 15, 726–751.Google Scholar
Pickard, D. K. (1982) Isolated nearest neighbors. J. Appl. Prob. 19, 444–449.Google Scholar
Roberts, F. D. K. (1969) Nearest neighbours in a Poisson ensemble. Biometrika 56, 401–406.Google Scholar
Rogers, W. H. and Wagner, T. J. (1978) A finite-sample, distribution-free performance bound for local discrimination rules. Ann. Statist. 6, 506–514.Google Scholar
Schilling, M. F. (1983) Goodness of fit testing in ℝ m based on the weighted empirical distribution of certain nearest neighbor statistics. Ann. Statist. 11, 1–12.Google Scholar
Schilling, M. F. (1986) Mutual and shared neighbor probabilities—finite and infinite-dimensional results. Adv. Appl. Prob. 18, 388–405.Google Scholar
Schwarz, G. and Tversky, A. (1980) On the reciprocity of proximity relations. J. Math. Psychol. 22, 157–175.Google Scholar
Stone, C. J. (1977) Consistent nonparametric regression. Ann. Statist. 5, 595–645.Google Scholar
Stute, W. (1984) Asymptotic normality of nearest neighbor regression function estimates. Ann. Statist. 12, 917–926.Google Scholar
Tversky, A. and Rinott, Y. (1983) Nearest neighbor analysis of point processes: Applications to multidimensional scaling. J. Math. Psychol. 27, 235–250.Google Scholar