Article contents
On a problem of ammunition rationing
Published online by Cambridge University Press: 01 July 2016
Abstract
Suppose you have u units of ammunition and want to destroy as many as possible of a sequence of attacking enemy aircraft. If you fire v = v(u), 0 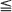 , units of your ammunition at the first enemy, it survives with probability qv, where 0 < q < 1 is given, and then kills you. With the complementary probability, 1 – qv, you destroy the aircraft and you live to face the next enemy with only u – v units of ammunition remaining. It seems almost obvious that any strategy which maximizes the expected number of enemies destroyed before you die will fire more units at the first enemy as u increases, i.e., it seems obvious that v′(u)
, units of your ammunition at the first enemy, it survives with probability qv, where 0 < q < 1 is given, and then kills you. With the complementary probability, 1 – qv, you destroy the aircraft and you live to face the next enemy with only u – v units of ammunition remaining. It seems almost obvious that any strategy which maximizes the expected number of enemies destroyed before you die will fire more units at the first enemy as u increases, i.e., it seems obvious that v′(u) 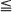 0 under optimal play. We show this to be false, thereby disproving an appealing conjecture proposed by Weber. We also consider a variant of this problem and find that the counterpart of Weber's conjecture holds in some cases.
0 under optimal play. We show this to be false, thereby disproving an appealing conjecture proposed by Weber. We also consider a variant of this problem and find that the counterpart of Weber's conjecture holds in some cases.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1991
Footnotes
Research supported by the National Science Foundation, Grant No. DMS-8701201.
References
- 5
- Cited by


