No CrossRef data available.
Article contents
A Monte Carlo algorithm for the extrema of tempered stable processes
Published online by Cambridge University Press: 30 June 2023
Abstract
We develop a novel Monte Carlo algorithm for the vector consisting of the supremum, the time at which the supremum is attained, and the position at a given (constant) time of an exponentially tempered Lévy process. The algorithm, based on the increments of the process without tempering, converges geometrically fast (as a function of the computational cost) for discontinuous and locally Lipschitz functions of the vector. We prove that the corresponding multilevel Monte Carlo estimator has optimal computational complexity (i.e. of order 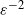 $\varepsilon^{-2}$ if the mean squared error is at most
$\varepsilon^{-2}$ if the mean squared error is at most 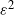 $\varepsilon^2$) and provide its central limit theorem (CLT). Using the CLT we construct confidence intervals for barrier option prices and various risk measures based on drawdown under the tempered stable (CGMY) model calibrated/estimated on real-world data. We provide non-asymptotic and asymptotic comparisons of our algorithm with existing approximations, leading to rule-of-thumb principles guiding users to the best method for a given set of parameters. We illustrate the performance of the algorithm with numerical examples.
$\varepsilon^2$) and provide its central limit theorem (CLT). Using the CLT we construct confidence intervals for barrier option prices and various risk measures based on drawdown under the tempered stable (CGMY) model calibrated/estimated on real-world data. We provide non-asymptotic and asymptotic comparisons of our algorithm with existing approximations, leading to rule-of-thumb principles guiding users to the best method for a given set of parameters. We illustrate the performance of the algorithm with numerical examples.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust



