Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T09:33:29.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for process-level Betti numbers for sparse and critical regimes

Part of: Geometric probability and stochastic geometry Algebraic combinatorics Applied homological algebra and category theory Limit theorems

Published online by Cambridge University Press:  29 April 2020

Takashi Owada  and
Andrew M. Thomas
Takashi Owada*
Affiliation:
Purdue University
Andrew M. Thomas*
Affiliation:
Purdue University
*
*Postal address: Department of Statistics, Purdue University, IN, 47907, USA
*Postal address: Department of Statistics, Purdue University, IN, 47907, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The objective of this study is to examine the asymptotic behavior of Betti numbers of Čech complexes treated as stochastic processes and formed from random points in the d-dimensional Euclidean space 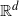${\mathbb{R}}^d$ . We consider the case where the points of the Čech complex are generated by a Poisson process with intensity nf for a probability density f. We look at the cases where the behavior of the connectivity radius of the Čech complex causes simplices of dimension greater than 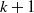$k+1$ to vanish in probability, the so-called sparse regime, as well when the connectivity radius is of the order of 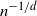$n^{-1/d}$ , the critical regime. We establish limit theorems in the aforementioned regimes: central limit theorems for the sparse and critical regimes, and a Poisson limit theorem for the sparse regime. When the connectivity radius of the Čech complex is 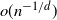$o(n^{-1/d})$ , i.e. the sparse regime, we can decompose the limiting processes into a time-changed Brownian motion or a time-changed homogeneous Poisson process respectively. In the critical regime, the limiting process is a centered Gaussian process but has a much more complicated representation, because the Čech complex becomes highly connected with many topological holes of any dimension.

Keywords

Random topologyBetti numbercentral limit theoremPoisson limit theorem

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 55U10: Simplicial sets and complexes 60F05: Central limit and other weak theorems 05E45: Combinatorial aspects of simplicial complexes
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 1 , March 2020 , pp. 1 - 31
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. J., Bobrowski, O., Borman, M. S., Subag, E. andWeinberger, S. (2010). Persistent homology for random fields and complexes. In Borrowing Strength: Theory Powering Applications; A Festschrift for Lawrence D. Brown, pp. 124–143. Institute of Mathematical Statistics.CrossRefGoogle Scholar
Adler, R. J., Bobrowski, O. andWeinberger, S. (2014). Crackle: the homology of noise. Discrete Comput. Geom. 52, 680–704.CrossRefGoogle Scholar
Billingsley, P. (1999). Convergence of Probability Measures, 2nd edn. Wiley, New York.CrossRefGoogle Scholar
Björner, A. (1995). Topological Methods. In Handbook of Combinatorics, vol. 2, eds R. L. Graham, M. Grötschel and L. Lovász, pp. 1819–1872. MIT Press, Cambridge, MA.Google Scholar
Bobrowski, O. andAdler, R. J. (2014). Distance functions, critical points, and the topology of random Čech complexes. Homology Homotopy Appl. 16, 311–344.CrossRefGoogle Scholar
Bobrowski, O. andKahle, M. (2018). Topology of random geometric complexes: a survey. J. Appl. Comput. Topology 1, 331–364.CrossRefGoogle Scholar
Bobrowski, O. andMukherjee, S. (2015). The topology of probability distributions on manifolds. Prob. Theory Relat. Fields 161, 651–686.CrossRefGoogle Scholar
Bobrowski, O. andWeinberger, S. (2017). On the vanishing of homology in random Čech complexes. Random Structures Algorithms 51, 14–51.CrossRefGoogle Scholar
Bobrowski, O., Kahle, M. andSkraba, P. (2017). Maximally persistent cycles in random geometric complexes. Ann. Appl. Prob. 27, 2032–2060.CrossRefGoogle Scholar
Carlsson, G. (2014). Topological pattern recognition for point cloud data. In Acta Numerica, vol. 23, pp. 289–368. Cambridge University Press.Google Scholar
Decreusefond, L., Ferraz, E., Randriambololona, H. andVergne, A. (2014). Simplicial homology of random configurations. Adv. Appl. Prob. 46, 325–347.CrossRefGoogle Scholar
Decreusefond, L., Schulte, M. andThäle, C. (2016). Functional Poisson approximation in Kantorovich–Rubinstein distance with applications to U-statistics and stochastic geometry. Ann. Prob. 44, 2147–2197.CrossRefGoogle Scholar
Durrett, R. (2010). Probability: Theory and Examples, 4th edn. Cambridge University Press.CrossRefGoogle Scholar
Edelsbrunner, H. andHarer, J. (2010). Computational Topology: An Introduction. American Mathematical Society.Google Scholar
Ghrist, R. (2008). Barcodes: The persistent topology of data. Bull. Amer. Math. Soc. 45, 61–76.CrossRefGoogle Scholar
Ghrist, R. W. (2014). Elementary Applied Topology. Createspace Seattle.Google Scholar
Goel, A., Trinh, K. D. andTsunoda, K. (2019). Strong law of large numbers for Betti numbers in the thermodynamic regime. J. Statist. Phys. 174, 865–892.CrossRefGoogle Scholar
Hatcher, A. (2001). Algebraic Topology. Cambridge University Press.Google Scholar
Hiraoka, Y., Shirai, T. andTrinh, K. D. (2018). Limit theorems for persistence diagrams. Ann. Appl. Prob. 28, 2740–2780.CrossRefGoogle Scholar
Kahle, M. (2011). Random geometric complexes. Discrete Comput. Geom. 45, 553–573.CrossRefGoogle Scholar
Kahle, M. andMeckes, E. (2013). Limit theorems for Betti numbers of random simplicial complexes. Homology Homotopy Appl. 15, 343–374.CrossRefGoogle Scholar
Kahle, M. andMeckes, E. (2016). Erratum to ‘Limit theorems for Betti numbers of random simplicial complexes’. Homology Homotopy Appl. 18, 129–142.CrossRefGoogle Scholar
Meester, R. andRoy, R. (1996). Continuum Percolation (Camb. Tracts. Math. 119). Cambridge University Press.CrossRefGoogle Scholar
Owada, T. (2017). Functional central limit theorem for subgraph counting processes. Electron. J. Prob. 22, 1–38, 17.CrossRefGoogle Scholar
Owada, T. (2018). Limit theorems for Betti numbers of extreme sample clouds with application to persistence barcodes. Ann. Appl. Prob. 28, 2814–2854.CrossRefGoogle Scholar
Penrose, M. (2003). Random Geometric Graphs. Oxford University Press.CrossRefGoogle Scholar
Penrose, M. D. andYukich, J. E. (2003). Weak laws of large numbers in geometric probability. Ann. Appl. Prob. 13, 277–303.CrossRefGoogle Scholar
Resnick, S. I. (1987). Extreme Values, Regular Variation and Point Processes. Springer, New York.CrossRefGoogle Scholar
Resnick, S. I. (2007). Heavy-Tail Phenomena: Probabilistic and Statistical Modeling. Springer, New York.Google Scholar
Trinh, K. D. (2017). A remark on the convergence of Betti numbers in the thermodynamic regime. Pacific J. Math. Ind. 9, 7.CrossRefGoogle Scholar
Trinh, K. D. (2018). On central limit theorems in stochastic geometry. Available at arXiv:1804.02823.Google Scholar
Wasserman, L. (2016). Topological data analysis. Ann. Rev. Statist. Appl. 5,501–532.CrossRefGoogle Scholar
Yogeshwaran, D. andAdler, R. J. (2015). On the topology of random complexes built over stationary point processes. Ann. Appl. Prob. 25, 3338–3380.CrossRefGoogle Scholar
Yogeshwaran, D., Subag, E. andAdler, R. J. (2017). Random geometric complexes in the thermodynamic regime. Prob. Theory Relat. Fields 167, 107–142.CrossRefGoogle Scholar
Zomorodian, A. andCarlsson, G. (2005). Computing persistent homology. Discrete Comput. Geom. 33, 249–274.CrossRefGoogle Scholar