Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T22:48:04.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit distributions of maximal segmental score among Markov-dependent partial sums

Part of: Limit theorems Special processes Stochastic processes

Published online by Cambridge University Press:  01 July 2016

Samuel Karlin  and
Amir Dembo
Samuel Karlin*
Affiliation:
Stanford University
Amir Dembo*
Affiliation:
Stanford University
*
∗Postal address: Department of Mathematics, Stanford University, Stanford, CA 94305, USA.
∗∗Postal address: Department of Statistics, Stanford University, Stanford, CA 94305, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

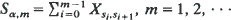Let s1, …, sn be generated governed by an r-state irreducible aperiodic Markov chain. The partial sum process is determined by a realization 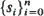of states with s0 = α and the real-valued i.i.d. bounded variables Xαß associated with the transitions si = α, si+1 = β. Assume Χ αβ has negative stationary mean. The explicit limit distribution of the maximal segmental sum 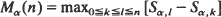is derived. Computational methods with potential applications to the analysis of random Markov-dependent letter sequences (e.g. DNA and protein sequences) are presented.

Keywords

MAXIMAL SEGMENTAL SUMSMARKOV-DEPENDENT WALD MARTINGALESMARKOV (WIENER-HOPF) THEORY

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60G70: Extreme value theory; extremal processes 60K15: Markov renewal processes, semi-Markov processes
Type
Research Article
Information
Advances in Applied Probability , Volume 24 , Issue 1 , March 1992 , pp. 113 - 140
Copyright
Copyright © Applied Probability Trust 1992 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partly supported by NIH Grants GM39907–02, GM10452–27, and NSF Grant DMS86–06244.

References

Altschul, S. F. and Lipman, D. J. (1990) Protein database searches for multiple alignments. Proc. Nat. Acad. Sci. USA 87, 5509–5513.CrossRefGoogle ScholarPubMed
Altschul, S. F., Gish, W., Miller, W., Myers, E. W. and Lipman, D. J. (1990) Local alignment search tool. J. Mol. Biol. 215, 403–417.CrossRefGoogle ScholarPubMed
Çinlar, E. (1975) Introduction to Stochastic Processes. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
Deheuvels, P. and Devroye, L. (1987) Limit laws of Erdös–Rényi–Shepp type. Ann. Prob. 15, 1363–1386.CrossRefGoogle Scholar
Dembo, A. and Karlin, S. (1991a) Limit distributions of empirical functionals for large exceedances of partial sum of i.i.d. variables. Ann. Prob. CrossRefGoogle Scholar
Dembo, A. and Karlin, S. (1991b) Limit theorems of empirical distributions for large segmental values of partial sums of Markov variables. Ann. Prob. Google Scholar
Feller, W. (1966) An Introduction to Probability Theory and Its Applications. Wiley, New York.Google Scholar
Foulser, D. E. and Karlin, S. (1987) Maximal success durations for a semi-Markov process. Stoch. Proc. Appl. 24, 203–224.Google Scholar
Iglehart, D. (1972) Extreme values in the GI/G/1 queue. Ann. Math. Statist. 43, 627–635.Google Scholar
Karlin, S. and Altschul, S. F. (1990) New methods for assessing statistical significance of molecular sequence features using general scoring schemes. Proc. Nat. Acad. Sci. USA 87, 2264–2268.Google Scholar
Karlin, S. and Ost, F. (1987) Counts of long aligned word matches among random letter sequences. Adv. Appl. Prob. 19, 293–351.Google Scholar
Karlin, S. and Taylor, H. M. (1981) A Second Course in Stochastic Processes. Academic Press, New York.Google Scholar
Karlin, S., Ost, S. and Blaisdell, B. E. (1989) Patterns in DNA and amino acid sequences and their statistical significance. In Mathematical Methods for DNA Sequences , Chapter 6. CRC Press, Boca Raton, FL.Google Scholar
Karlin, S., Dembo, A. and Kawabata, T. (1990) Statistical composition of high scoring segments from molecular sequences. Ann. Statist. 16, 547–556.Google Scholar
Karlin, S., Bucher, P., Brendel, V. and Altschul, S. F. (1991) Statistical methods and insights for protein and DNA sequences. Ann. Rev. Biophys. Biophys. Chem. 20, 175–203.Google Scholar
Ney, P. and Nummelin, E. (1987a) Markov additive processes. I. Eigenvalues properties and limit theorems. Ann. Prob. 15, 561–582.Google Scholar
Ney, P. and Nummelin, E. (1987b) Markov additive processes. II. Large deviations. Ann. Prob. 15, 593–609.CrossRefGoogle Scholar
Róotzen, H. (1988) Maxima and exceedances of stationary Markov chains. Adv. Appl. Prob. 20, 371–390.Google Scholar
Siegmund, D. (1988) Approximate tail probabilities for the maxima of some random fields. Ann. Prob. 16. 487–501.Google Scholar
Spitzer, F. (1960) A Tauberian theorem and its probability interpretation. Trans. Amer. Math. Soc. 94, 150–169.Google Scholar