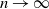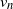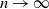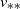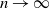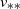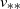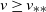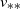1. Introduction
1.1. Model, motivation, and (informally) main results
We consider a system consisting of n particles, moving forward in jumps on the real line. A particle can jump either independently or via ‘synchronizations’ with other particles. Independent jumps of a particle occur at time points of an independent Poisson process of constant rate
![]() $\lambda \ge 0$
; the jump sizes are independent and identically distributed as a random variable
$\lambda \ge 0$
; the jump sizes are independent and identically distributed as a random variable
![]() $Z>0$
with cumulative distribution function
$Z>0$
with cumulative distribution function
![]() $J({\cdot})$
and finite mean,
$J({\cdot})$
and finite mean,
![]() $\mathbb{E} Z < \infty$
; without loss of generality we can and do assume
$\mathbb{E} Z < \infty$
; without loss of generality we can and do assume
![]() $\mathbb{E} Z =1$
. Each particle also has another independent Poisson process (of synchronizations), of constant rate
$\mathbb{E} Z =1$
. Each particle also has another independent Poisson process (of synchronizations), of constant rate
![]() $\mu>0$
, at which points it chooses another particle uniformly at random, and makes a synchronization jump to the location of the chosen particle if the latter is ahead—to the right—of its own current location. The system state at a given time is the empirical distribution of particle locations. We focus on the mean-field asymptotic regime where n becomes large.
$\mu>0$
, at which points it chooses another particle uniformly at random, and makes a synchronization jump to the location of the chosen particle if the latter is ahead—to the right—of its own current location. The system state at a given time is the empirical distribution of particle locations. We focus on the mean-field asymptotic regime where n becomes large.
Our model is of the type in which particles move both autonomously (independent jumps) and according to a synchronization mechanism. (See [Reference Balázs, Rácz and Tóth1, Reference Greenberg, Malyshev and Popov11–Reference Groisman, Jonckheere and Martínez13, Reference Malyshev and Manita17–Reference Manita and Shcherbakov22] and references therein for previous models of this type.) Such models are motivated by distributed systems, in which agents need to both evolve and synchronize their states, and the synchronization is accomplished in a distributed fashion, via random peer-to-peer communication. The special feature of our model is that, even in the asymptotic limit, the autonomous movement of a particle is discontinuous (consists of random jumps). This brings up the question of how much the synchronization mechanism affects the overall speed of advance of the system, and of what constitutes a good trade-off between the ‘self-propulsion’ (independent jump) rate and the synchronization rate. In models of technological systems, such as parallel computing/simulation or wireless systems (cf. [Reference Greenberg, Malyshev and Popov11, Reference Greenberg, Shenker and Stolyar12, Reference Malyshev and Manita17–Reference Manita and Shcherbakov22]), particles’ locations correspond to agents’ local ‘clocks’, which advance locally but need to be synchronized. Our specific system can also model a business environment, with multiple companies that can improve their products either via investments in themselves (‘self-propulsion’) or via acquisitions (‘synchronization’).
The main question that we address in this paper is very typical for this kind of system: as n becomes large, what is the average speed at which the system state (empirical distribution) moves forward? Specifically, we will be interested in two metrics of the speed of advance: the steady-state speed of advance
![]() $v_n$
, especially
$v_n$
, especially
![]() $\lim_{n\to\infty} v_n$
; and the average speed of the mean-field limit (MFL), which, informally speaking, is the deterministic limit of the system state dynamics as
$\lim_{n\to\infty} v_n$
; and the average speed of the mean-field limit (MFL), which, informally speaking, is the deterministic limit of the system state dynamics as
![]() $n\to\infty$
. Our main results are as follows:
$n\to\infty$
. Our main results are as follows:
-
• We prove that
 $v_n \to v_{**}$
as
$v_n \to v_{**}$
as
 ${n\to\infty}$
, where the value of
${n\to\infty}$
, where the value of
 $v_{**}$
can easily be found from a minimum speed selection principle.
$v_{**}$
can easily be found from a minimum speed selection principle. -
• We prove that as
 $n\to\infty$
, the system dynamics converges to that of a deterministic MFL. We also prove this for two modified systems, with a left or right boundary moving at a constant speed v.
$n\to\infty$
, the system dynamics converges to that of a deterministic MFL. We also prove this for two modified systems, with a left or right boundary moving at a constant speed v. -
• We show that the average speed of advance of any MFL is lower-bounded by
 $v_{**}$
, and the speed of a ‘benchmark’ MFL (BMFL), resulting from all particles initially being co-located, is equal to
$v_{**}$
, and the speed of a ‘benchmark’ MFL (BMFL), resulting from all particles initially being co-located, is equal to
 $v_{**}$
.
$v_{**}$
. -
• In the special case of exponentially distributed independent jump sizes, we obtain the following:
-
– We prove that a traveling-wave MFL with speed v exists if and only if
 $v\ge v_{**}$
, with
$v\ge v_{**}$
, with
 $v_{**}$
having a very simple explicit form. In addition, we show that a traveling wave with moving left boundary exists for any boundary speed
$v_{**}$
having a very simple explicit form. In addition, we show that a traveling wave with moving left boundary exists for any boundary speed
 $v > v_{**}$
, and a traveling wave with moving right boundary exists for any boundary speed
$v > v_{**}$
, and a traveling wave with moving right boundary exists for any boundary speed
 $v < v_{**}$
.
$v < v_{**}$
. -
– Using monotonicity and the traveling waves as bounds, we obtain bounds on an MFL’s average speed of advance, depending on the right tail exponent of the initial state.
-
We conjecture that the above results for exponential jump sizes extend to general jump sizes as well.
Using our results, in a large-scale system, one can easily optimize a trade-off between
![]() $\lambda$
and
$\lambda$
and
![]() $\mu$
(between self-propulsion and synchronization efforts) to achieve maximum speed. For example, one can maximize
$\mu$
(between self-propulsion and synchronization efforts) to achieve maximum speed. For example, one can maximize
![]() $v_{**} = v_{**}(\lambda,\mu)$
subject to
$v_{**} = v_{**}(\lambda,\mu)$
subject to
![]() $a \lambda + b \mu \le 1$
, where the constants
$a \lambda + b \mu \le 1$
, where the constants
![]() $a>0$
and
$a>0$
and
![]() $b>0$
describe the unit rates at which self-propulsion and synchronization consume some common resource. We provide simulation results illustrating that this approach works well when the number of particles is large.
$b>0$
describe the unit rates at which self-propulsion and synchronization consume some common resource. We provide simulation results illustrating that this approach works well when the number of particles is large.
1.2. Previous work and discussion of our results
The literature on the mean-field asymptotic behavior of large-scale particle systems is vast. We will only describe the previous work that is most closely related; the reader will find further literature reviews in the works cited here.
An MFL is a function
![]() $(f_x(t), \,x\in \mathbb{R}, \,t\ge 0)$
, where
$(f_x(t), \,x\in \mathbb{R}, \,t\ge 0)$
, where
![]() $(f_x(t), \,x\in \mathbb{R})$
is the cumulative distribution function of particle locations on the real line at time t, in the
$(f_x(t), \,x\in \mathbb{R})$
is the cumulative distribution function of particle locations on the real line at time t, in the
![]() $n\to\infty$
limit. Thus, it describes the ‘macro-behavior’ of a particle system. (The term ‘micro-behavior’ often refers to the evolution of the system when the number n of particles is finite.)
$n\to\infty$
limit. Thus, it describes the ‘macro-behavior’ of a particle system. (The term ‘micro-behavior’ often refers to the evolution of the system when the number n of particles is finite.)
It is well known that the classical Kolmogorov–Petrovskii–Piscounov (KPP) equation [Reference Kolmogorov, Petrovskii and Piscounov15],
describes MFLs (in our terminology) of many large-scale particle systems (cf. [Reference Groisman, Jonckheere and Martínez13, Reference Manita and Shcherbakov22] and references therein). In (1.1),
![]() $F({\cdot})$
is a non-positive function within a certain class (for example,
$F({\cdot})$
is a non-positive function within a certain class (for example,
![]() $F(y) = -y(1-y)$
or
$F(y) = -y(1-y)$
or
![]() $F(y) = -y(1-y^2)$
). The seminal paper [Reference Kolmogorov, Petrovskii and Piscounov15] studies Equation (1.1) and proves, in particular, that Equation (1.1) has traveling-wave solutions with any speed
$F(y) = -y(1-y^2)$
). The seminal paper [Reference Kolmogorov, Petrovskii and Piscounov15] studies Equation (1.1) and proves, in particular, that Equation (1.1) has traveling-wave solutions with any speed
![]() $v \ge v_{**}$
, where the minimum speed
$v \ge v_{**}$
, where the minimum speed
![]() $v_{**}$
depends on function
$v_{**}$
depends on function
![]() $F({\cdot})$
; it is also proved that
$F({\cdot})$
; it is also proved that
![]() $v_{**}$
is the average speed of the solution with initial condition being a Dirac distribution concentrated at 0 (we refer to such a solution as the benchmark MFL (BMFL)). It has since been found (cf. [Reference Bramson4–Reference Brunet and Derrida6, Reference Groisman, Jonckheere and Martínez13] and references therein) that in many instances, a particle system having KPP as its MFL (or, in fact, a different asymptotic limit) is such that the steady-state particle system speed
$v_{**}$
is the average speed of the solution with initial condition being a Dirac distribution concentrated at 0 (we refer to such a solution as the benchmark MFL (BMFL)). It has since been found (cf. [Reference Bramson4–Reference Brunet and Derrida6, Reference Groisman, Jonckheere and Martínez13] and references therein) that in many instances, a particle system having KPP as its MFL (or, in fact, a different asymptotic limit) is such that the steady-state particle system speed
![]() $v_n$
satisfies
$v_n$
satisfies
![]() $\lim_{n\to\infty} v_n = v_{**}$
. In other words, the micro-behavior is such that the system ‘selects the minimum speed of the traveling waves that can arise in macro-behavior’. This is sometimes referred to as a minimum speed selection principle (MSSP) [Reference Brunet and Derrida5, Reference Brunet and Derrida6]. In this paper we show that the same basic phenomenon holds for our system, even though its macro-behavior (i.e., the MFL dynamics equation), even in the special case of exponential jumps, is not within the KPP class. Our proof of the traveling-wave existence results for exponential jumps, while it follows the general approach of KPP [Reference Kolmogorov, Petrovskii and Piscounov15] (i.e., analysis of the phase portrait of a two-dimensional ordinary differential equation (ODE)), requires new observations—in particular, the use of parabolic (as opposed to linear) barriers.
$\lim_{n\to\infty} v_n = v_{**}$
. In other words, the micro-behavior is such that the system ‘selects the minimum speed of the traveling waves that can arise in macro-behavior’. This is sometimes referred to as a minimum speed selection principle (MSSP) [Reference Brunet and Derrida5, Reference Brunet and Derrida6]. In this paper we show that the same basic phenomenon holds for our system, even though its macro-behavior (i.e., the MFL dynamics equation), even in the special case of exponential jumps, is not within the KPP class. Our proof of the traveling-wave existence results for exponential jumps, while it follows the general approach of KPP [Reference Kolmogorov, Petrovskii and Piscounov15] (i.e., analysis of the phase portrait of a two-dimensional ordinary differential equation (ODE)), requires new observations—in particular, the use of parabolic (as opposed to linear) barriers.
The first paper to formally prove an MSSP for a particle system with macro-behavior within the KPP class is [Reference Bramson4]. The recent paper [Reference Groisman, Jonckheere and Martínez13] considers a particle system which is just like ours, but the independent movement of each particle is a Brownian motion (instead of forward jumps); the paper shows that the MFLs of the system are within the KPP class, and proves the MSSP for it. The MSSP is not limited to particle systems whose macro-behavior is within the KPP class. For example, the paper [Reference Durrett and Remenik7] proves the MSSP for a branching selection process whose MFL is described by an integro-differential equation with free left boundary; it proves, in particular, a traveling-wave existence result for all speeds greater than or equal to a critical speed. We note that the auxiliary systems with moving left and right boundaries are substantially different from the moving free boundary arising in MFL dynamics in [Reference Durrett and Remenik7]: our boundaries are ‘reflecting’, rather than ‘absorbing’.
The proofs of the fact that
![]() $\lim v_n = v_{**}$
in [Reference Durrett and Remenik7, Reference Groisman, Jonckheere and Martínez13] (see also references therein) rely on system monotonicity properties and on the relationship with a corresponding branching process, which is either a branching Brownian motion or a branching random walk (BRW). In fact, the critical speed
$\lim v_n = v_{**}$
in [Reference Durrett and Remenik7, Reference Groisman, Jonckheere and Martínez13] (see also references therein) rely on system monotonicity properties and on the relationship with a corresponding branching process, which is either a branching Brownian motion or a branching random walk (BRW). In fact, the critical speed
![]() $v_{**}$
is the average speed of advance of the leading (rightmost) particle of the branching process. Our proof that
$v_{**}$
is the average speed of advance of the leading (rightmost) particle of the branching process. Our proof that
![]() $\limsup v_n = v_{**}$
is essentially the same as the proofs in [Reference Durrett and Remenik7, Reference Groisman, Jonckheere and Martínez13], except that the corresponding BRW in our case is different; our proof that
$\limsup v_n = v_{**}$
is essentially the same as the proofs in [Reference Durrett and Remenik7, Reference Groisman, Jonckheere and Martínez13], except that the corresponding BRW in our case is different; our proof that
![]() $\liminf v_n = v_{**}$
is related to, but different from, the proof of the corresponding property in [Reference Durrett and Remenik7].
$\liminf v_n = v_{**}$
is related to, but different from, the proof of the corresponding property in [Reference Durrett and Remenik7].
As we just mentioned, the critical speed
![]() $v_{**}$
is the average speed of advance of the leading (rightmost) particle of the branching process. McKean [Reference McKean23] found that the BMFL for a KPP equation [Reference Kolmogorov, Petrovskii and Piscounov15] is such that
$v_{**}$
is the average speed of advance of the leading (rightmost) particle of the branching process. McKean [Reference McKean23] found that the BMFL for a KPP equation [Reference Kolmogorov, Petrovskii and Piscounov15] is such that
![]() $(f_x(t), \,x\in \mathbb{R})$
is the distribution of the leading particle location for the associated branching Brownian motion with the initial particle location at 0; we need and provide an analogous characterization of the BMFL for our system in terms of the corresponding BRW. For a general discrete-time BRW, the average speed
$(f_x(t), \,x\in \mathbb{R})$
is the distribution of the leading particle location for the associated branching Brownian motion with the initial particle location at 0; we need and provide an analogous characterization of the BMFL for our system in terms of the corresponding BRW. For a general discrete-time BRW, the average speed
![]() $v_{**}$
of the leading particle (as well as that of the trailing particle) was found by Biggins [Reference Biggins3] (who extended the results of Kingman [Reference Kingman14]); the average speed
$v_{**}$
of the leading particle (as well as that of the trailing particle) was found by Biggins [Reference Biggins3] (who extended the results of Kingman [Reference Kingman14]); the average speed
![]() $v_{**}$
of the leading particle of the continuous-time BRW in our case follows from the results of [Reference Biggins3].
$v_{**}$
of the leading particle of the continuous-time BRW in our case follows from the results of [Reference Biggins3].
The line of work in [Reference Freidlin9, Reference Freidlin10, Reference Larson16, Reference Veretennikov27] is concerned with the speed of the solutions (MFLs) of the KPP equation [Reference Kolmogorov, Petrovskii and Piscounov15], depending on the initial condition or, more precisely, the exponent of the right tail of the initial condition. The key results show that any speed
![]() $v \ge v_{**}$
can be achieved. In [Reference Larson16] this is shown via direct analysis of the KPP solutions [Reference Kolmogorov, Petrovskii and Piscounov15], while [Reference Freidlin9, Reference Freidlin10, Reference Veretennikov27] use a Feynman–Kac representation of a solution and a large-deviations approach. We obtain analogous results for our system, under the additional assumption of exponential jumps, but our approach is completely different: we prove the existence of traveling waves, including waves with moving boundaries, and use these traveling waves as lower and upper bounds of MFLs. We note that our approach can be applied to the KPP solutions [Reference Kolmogorov, Petrovskii and Piscounov15] as well, because the existence of traveling waves with moving boundaries for KPP can be obtained from [Reference Kolmogorov, Petrovskii and Piscounov15] in the same way as we do for our model. In particular, we believe this gives alternative proofs of many of the MFL speed results in [Reference Freidlin9, Reference Freidlin10, Reference Larson16, Reference Veretennikov27], and it should be applicable to other models as well.
$v \ge v_{**}$
can be achieved. In [Reference Larson16] this is shown via direct analysis of the KPP solutions [Reference Kolmogorov, Petrovskii and Piscounov15], while [Reference Freidlin9, Reference Freidlin10, Reference Veretennikov27] use a Feynman–Kac representation of a solution and a large-deviations approach. We obtain analogous results for our system, under the additional assumption of exponential jumps, but our approach is completely different: we prove the existence of traveling waves, including waves with moving boundaries, and use these traveling waves as lower and upper bounds of MFLs. We note that our approach can be applied to the KPP solutions [Reference Kolmogorov, Petrovskii and Piscounov15] as well, because the existence of traveling waves with moving boundaries for KPP can be obtained from [Reference Kolmogorov, Petrovskii and Piscounov15] in the same way as we do for our model. In particular, we believe this gives alternative proofs of many of the MFL speed results in [Reference Freidlin9, Reference Freidlin10, Reference Larson16, Reference Veretennikov27], and it should be applicable to other models as well.
In terms of motivation, this paper is closely related to the work on models where a degree of ‘synchronization’ is desired, meaning that the collection of particles remains ‘tight’; specifically, most particles remain within O(1) distance of each other, uniformly in n. This includes the ‘rank-based’ model in [Reference Greenberg, Malyshev and Popov11, Reference Greenberg, Shenker and Stolyar12, Reference Stolyar25, Reference Stolyar26], where the instantaneous rate at which a particle jumps forward is a non-increasing function of the particle’s location quantile within the empirical distribution of all of the particles’ locations. The results of [Reference Greenberg, Malyshev and Popov11, Reference Greenberg, Shenker and Stolyar12, Reference Stolyar25, Reference Stolyar26] establish most of the properties of interest: convergence to an MFL as
![]() $n\to\infty$
; convergence of an MFL to a traveling wave as time goes to infinity; and convergence of stationary distributions to a Dirac distribution concentrated on a traveling wave. Other models of distributed synchronization include those in, e.g., [Reference Balázs, Rácz and Tóth1, Reference Malyshev and Manita17–Reference Manita and Shcherbakov22]. The paper [Reference Balázs, Rácz and Tóth1] considers a ‘barycentric’ model, where the instantaneous rate at which a particle jumps forward is a non-increasing function of the particle’s location displacement from the mean of the empirical distribution of all of the particles’ locations; it establishes (under certain conditions) the results on convergence to the MFL, and it finds traveling-wave forms in some special cases. From a technical point of view, our proofs of convergence to the MFL and its uniqueness closely follow the approach used in [Reference Balázs, Rácz and Tóth1, Reference Stolyar25]. The paper [Reference Stolyar26] employs an artificial system with moving ‘reflecting’ boundaries as a tool for analysis of the original system; this approach is one of the tools used in the present paper as well.
$n\to\infty$
; convergence of an MFL to a traveling wave as time goes to infinity; and convergence of stationary distributions to a Dirac distribution concentrated on a traveling wave. Other models of distributed synchronization include those in, e.g., [Reference Balázs, Rácz and Tóth1, Reference Malyshev and Manita17–Reference Manita and Shcherbakov22]. The paper [Reference Balázs, Rácz and Tóth1] considers a ‘barycentric’ model, where the instantaneous rate at which a particle jumps forward is a non-increasing function of the particle’s location displacement from the mean of the empirical distribution of all of the particles’ locations; it establishes (under certain conditions) the results on convergence to the MFL, and it finds traveling-wave forms in some special cases. From a technical point of view, our proofs of convergence to the MFL and its uniqueness closely follow the approach used in [Reference Balázs, Rácz and Tóth1, Reference Stolyar25]. The paper [Reference Stolyar26] employs an artificial system with moving ‘reflecting’ boundaries as a tool for analysis of the original system; this approach is one of the tools used in the present paper as well.
Finally, we note that the papers [Reference Brunet and Derrida5, Reference Brunet and Derrida6] provided the first explanation of the phenomenon of ‘slow convergence’ of steady-state speeds,
![]() $v_n \to v_{**}$
, for particle systems having KPP solutions as MFLs. The first formal proof of this phenomenon was given, for a closely related particle system, in [Reference Berard and Gouere2]. Our simulations indicate that this phenomenon occurs in our system as well; proving this rigorously may be a subject of future work.
$v_n \to v_{**}$
, for particle systems having KPP solutions as MFLs. The first formal proof of this phenomenon was given, for a closely related particle system, in [Reference Berard and Gouere2]. Our simulations indicate that this phenomenon occurs in our system as well; proving this rigorously may be a subject of future work.
1.3. Outline of the rest of the paper
Section 2 gives basic notation used throughout the paper. In Section 3 we formally define the system process and describe its basic properties, while Section 4 specifically focuses on the important monotonicity properties. Section 5 presents our results on the convergence to—and properties of—mean-field limits (MFLs). Section 6 defines traveling waves. In Section 7 we formally define the critical speed
![]() $v_{**}$
via a minimum speed selection principle (MSSP). In Section 8 we define the associated BRW, give a McKean-type characterization of the original system’s BMFL in terms of this BRW, and show that
$v_{**}$
via a minimum speed selection principle (MSSP). In Section 8 we define the associated BRW, give a McKean-type characterization of the original system’s BMFL in terms of this BRW, and show that
![]() $v_{**}$
is equal to the average speed of the leading particle of the BRW; finally, we present the result that
$v_{**}$
is equal to the average speed of the leading particle of the BRW; finally, we present the result that
![]() $\lim v_n = v_{**}$
. In Section 9 we state the traveling-wave existence results in the special case of exponentially distributed jumps. In Section 10 we present the results on the MFL speeds: the lower bound
$\lim v_n = v_{**}$
. In Section 9 we state the traveling-wave existence results in the special case of exponentially distributed jumps. In Section 10 we present the results on the MFL speeds: the lower bound
![]() $v_{**}$
, which holds for general jump size distribution, and speed bounds for exponential-jumps case, which depend on the right tail exponent of the initial state. In Section 11 we state some further conjectures and present simulation results. Sections 12–20 contain proofs.
$v_{**}$
, which holds for general jump size distribution, and speed bounds for exponential-jumps case, which depend on the right tail exponent of the initial state. In Section 11 we state some further conjectures and present simulation results. Sections 12–20 contain proofs.
2. Basic notation
The set of real numbers is denoted by
![]() $\mathbb{R}$
and is viewed as the usual Euclidean space. As a measurable space,
$\mathbb{R}$
and is viewed as the usual Euclidean space. As a measurable space,
![]() $\mathbb{R}$
is endowed with the Borel
$\mathbb{R}$
is endowed with the Borel
![]() $\sigma$
-algebra. For scalar functions g(x) of a real x, we write
$\sigma$
-algebra. For scalar functions g(x) of a real x, we write
![]() $\|g\|_1 = \int_x |g(x)|dx$
for the
$\|g\|_1 = \int_x |g(x)|dx$
for the
![]() $L_1$
-norm; g(x) is called c-Lipschitz if it is Lipschitz with constant
$L_1$
-norm; g(x) is called c-Lipschitz if it is Lipschitz with constant
![]() $c \ge 0$
. Let
$c \ge 0$
. Let
![]() $\mathcal{C}_b$
be the set of continuous bounded functions on
$\mathcal{C}_b$
be the set of continuous bounded functions on
![]() $\mathbb{R}$
which are constant outside a closed interval (with one constant value to the ‘left’ of the interval, and possibly another constant value to the ‘right’ of it.)
$\mathbb{R}$
which are constant outside a closed interval (with one constant value to the ‘left’ of the interval, and possibly another constant value to the ‘right’ of it.)
For functions g(x) of a real x, we denote by
![]() $g(x+)$
and
$g(x+)$
and
![]() $g(x-)$
the right and left limits at x; a function g(x) is RCLL if it is right-continuous and has left limits at each x.
$g(x-)$
the right and left limits at x; a function g(x) is RCLL if it is right-continuous and has left limits at each x.
A function g of x may be written as either g(x) or
![]() $g_x$
. The notation
$g_x$
. The notation
![]() $d_x g(x,t)$
for a multivariate function g(x,t), where
$d_x g(x,t)$
for a multivariate function g(x,t), where
![]() $x\in \mathbb{R}$
, means the differential in x.
$x\in \mathbb{R}$
, means the differential in x.
Denote by
![]() $\mathcal{M}$
the set of scalar RCLL non-decreasing functions
$\mathcal{M}$
the set of scalar RCLL non-decreasing functions
![]() $f=(f(x), x\in \mathbb{R})$
that are (proper) probability distribution functions, i.e., such that
$f=(f(x), x\in \mathbb{R})$
that are (proper) probability distribution functions, i.e., such that
![]() $f(x) \in [0,1]$
,
$f(x) \in [0,1]$
,
![]() $\lim_{x\downarrow -\infty} f(x) = 0$
, and
$\lim_{x\downarrow -\infty} f(x) = 0$
, and
![]() $\lim_{x\uparrow \infty} f(x) = 1$
. For elements
$\lim_{x\uparrow \infty} f(x) = 1$
. For elements
![]() $f \in \mathcal{M}$
we use the terms distribution function and distribution interchangeably. The space
$f \in \mathcal{M}$
we use the terms distribution function and distribution interchangeably. The space
![]() $\mathcal{M}$
is endowed with the Lévy–Prokhorov metric (cf. [Reference Ethier and Kurtz8]) and the corresponding topology of weak convergence (which is equivalent to the convergence at every point of continuity of the limit); the weak convergence in
$\mathcal{M}$
is endowed with the Lévy–Prokhorov metric (cf. [Reference Ethier and Kurtz8]) and the corresponding topology of weak convergence (which is equivalent to the convergence at every point of continuity of the limit); the weak convergence in
![]() $\mathcal{M}$
is denoted
$\mathcal{M}$
is denoted
![]() $\stackrel{w}{\rightarrow}$
. Subspaces of
$\stackrel{w}{\rightarrow}$
. Subspaces of
![]() $\mathcal{M}$
that we define later inherit its metric. The inverse (
$\mathcal{M}$
that we define later inherit its metric. The inverse (
![]() $\nu$
th quantile) of
$\nu$
th quantile) of
![]() $f \in \mathcal{M}$
is
$f \in \mathcal{M}$
is
![]() $f_{\nu}^{-1} \doteq \inf\{y\,|\,f_y \ge \nu\}$
,
$f_{\nu}^{-1} \doteq \inf\{y\,|\,f_y \ge \nu\}$
,
![]() $\nu\in [0,1]$
;
$\nu\in [0,1]$
;
![]() $f_1^{-1} =\infty$
when
$f_1^{-1} =\infty$
when
![]() $f_y < 1$
for all y; we will also use the notation
$f_y < 1$
for all y; we will also use the notation
![]() $q_\nu(f) \doteq f_{\nu}^{-1} $
. For a given
$q_\nu(f) \doteq f_{\nu}^{-1} $
. For a given
![]() $\nu\in (0,1)$
, set
$\nu\in (0,1)$
, set
![]() $\mathring{\mathcal{M}} = \{f \in \mathcal{M} \,|\, f_{\nu}^{-1} =0\}$
; the parameter
$\mathring{\mathcal{M}} = \{f \in \mathcal{M} \,|\, f_{\nu}^{-1} =0\}$
; the parameter
![]() $\nu$
used in the definition of
$\nu$
used in the definition of
![]() $\mathring{\mathcal{M}}$
will be clear from the context.
$\mathring{\mathcal{M}}$
will be clear from the context.
Unless explicitly specified otherwise, we use the following conventions regarding random elements and random processes. A measurable space is assumed to be equipped with the Borel
![]() $\sigma$
-algebra induced by the metric, which is clear from the context. A random process
$\sigma$
-algebra induced by the metric, which is clear from the context. A random process
![]() $Y(t), \,t\ge 0,$
always takes values in a complete separable metric space (clear from the context) and has RCLL sample paths. For a random process
$Y(t), \,t\ge 0,$
always takes values in a complete separable metric space (clear from the context) and has RCLL sample paths. For a random process
![]() $Y(t), \,t\ge 0,$
we denote by
$Y(t), \,t\ge 0,$
we denote by
![]() $Y(\infty)$
the random value of Y(t) in a stationary regime (which will be clear from the context). The symbol
$Y(\infty)$
the random value of Y(t) in a stationary regime (which will be clear from the context). The symbol
![]() $\Rightarrow$
signifies convergence of random elements in distribution;
$\Rightarrow$
signifies convergence of random elements in distribution;
![]() $\stackrel{\mathbb{P}}{\longrightarrow}$
means convergence in probability. For a condition/event A,
$\stackrel{\mathbb{P}}{\longrightarrow}$
means convergence in probability. For a condition/event A,
![]() ${\mathbf{I}}\{A\}=1$
if A holds, and
${\mathbf{I}}\{A\}=1$
if A holds, and
![]() ${\mathbf{I}}\{A\}=0$
otherwise.
${\mathbf{I}}\{A\}=0$
otherwise.
The space
![]() $D([0,\infty), \mathbb{R})$
(resp.
$D([0,\infty), \mathbb{R})$
(resp.
![]() $D([0,\infty), \mathcal{M})$
) is the Skorokhod space of RCLL functions on
$D([0,\infty), \mathcal{M})$
) is the Skorokhod space of RCLL functions on
![]() $[0,\infty)$
taking values in
$[0,\infty)$
taking values in
![]() $\mathbb{R}$
[resp.
$\mathbb{R}$
[resp.
![]() $\mathcal{M}$
], with the corresponding Skorokhod (
$\mathcal{M}$
], with the corresponding Skorokhod (
![]() $J_1$
) metric and topology (cf. [Reference Ethier and Kurtz8]); the symbol
$J_1$
) metric and topology (cf. [Reference Ethier and Kurtz8]); the symbol
![]() $\stackrel{J_1}{\rightarrow}$
denotes convergence in these spaces.
$\stackrel{J_1}{\rightarrow}$
denotes convergence in these spaces.
For a distribution
![]() $f \in \mathcal{M}$
and scalar function
$f \in \mathcal{M}$
and scalar function
![]() $h(x), x \in \mathbb{R}$
, we define
$h(x), x \in \mathbb{R}$
, we define
![]() $f h \doteq \int_{\mathbb{R}} h(x) df_x$
. In some cases it is important whether or not an integral includes the endpoints of the integration interval;
$f h \doteq \int_{\mathbb{R}} h(x) df_x$
. In some cases it is important whether or not an integral includes the endpoints of the integration interval;
![]() $\int_{a+}^b h(x) df_x$
means that the integral excludes the left endpoint a, and
$\int_{a+}^b h(x) df_x$
means that the integral excludes the left endpoint a, and
![]() $\int_{a}^{b+} h(x) df_x$
means that the integral includes the right endpoint b.
$\int_{a}^{b+} h(x) df_x$
means that the integral includes the right endpoint b.
For scalar functions
![]() $h(x), x \in \mathcal{X}$
, with some domain
$h(x), x \in \mathcal{X}$
, with some domain
![]() $\mathcal{X}$
,
$\mathcal{X}$
,
![]() $\|h\| = \sup_{x\in \mathcal{X}} |h(x)|$
is the sup-norm. When
$\|h\| = \sup_{x\in \mathcal{X}} |h(x)|$
is the sup-norm. When
![]() $G_k, G$
are operators mapping the space of such functions into itself,
$G_k, G$
are operators mapping the space of such functions into itself,
![]() $\lim G_k h = Gh$
and
$\lim G_k h = Gh$
and
![]() $G_k h \to Gh$
mean uniform convergence:
$G_k h \to Gh$
mean uniform convergence:
![]() $\|G_k h - Gh\| \to 0$
.
$\|G_k h - Gh\| \to 0$
.
Suppose we have a Markov process with state space
![]() $\mathcal{X}$
and transition function
$\mathcal{X}$
and transition function
![]() $P^t(x,H),$
$P^t(x,H),$
![]() $t\ge 0$
. Then
$t\ge 0$
. Then
![]() $P^t$
, as an operator, is
$P^t$
, as an operator, is
![]() $P^t h(x) \doteq \int_y P^t(x,dy) h(y)$
, where h is a scalar function with domain
$P^t h(x) \doteq \int_y P^t(x,dy) h(y)$
, where h is a scalar function with domain
![]() $\mathcal{X}$
;
$\mathcal{X}$
;
![]() $I=P^0$
is the identity operator. The process (infinitesimal) generator B is
$I=P^0$
is the identity operator. The process (infinitesimal) generator B is
The function h is within the domain of the generator B if Bh is well-defined.
We denote by
![]() $\bar J(x) = 1- J(x)$
the complementary cumulative distribution function of the jump size distribution. The Heaviside step function (or Dirac distribution concentrated at the point 0) is denoted by
$\bar J(x) = 1- J(x)$
the complementary cumulative distribution function of the jump size distribution. The Heaviside step function (or Dirac distribution concentrated at the point 0) is denoted by
![]() $\chi=(\chi_x = {\mathbf{I}}\{x \ge 0\}) \in \mathcal{M}$
.
$\chi=(\chi_x = {\mathbf{I}}\{x \ge 0\}) \in \mathcal{M}$
.
3. System process definition
We already noted that, without loss of generality, we may assume
![]() $\mathbb{E} Z= 1$
; otherwise, this condition can be achieved by rescaling space. Note also that, without loss of generality, we can and do assume
$\mathbb{E} Z= 1$
; otherwise, this condition can be achieved by rescaling space. Note also that, without loss of generality, we can and do assume
![]() $\mu=1$
; otherwise, we can achieve this condition by rescaling time.
$\mu=1$
; otherwise, we can achieve this condition by rescaling time.
Let
![]() $f^n(t) =(f_x^n(t), \,x\in \mathbb{R})$
be the (random) empirical distribution of the particle locations at time t; that is,
$f^n(t) =(f_x^n(t), \,x\in \mathbb{R})$
be the (random) empirical distribution of the particle locations at time t; that is,
![]() $f_x^n(t)$
is the fraction of particles located in
$f_x^n(t)$
is the fraction of particles located in
![]() $({-}\infty,x]$
at time t. Clearly,
$({-}\infty,x]$
at time t. Clearly,
![]() $f^n({\cdot})$
is a Markov process with the state space
$f^n({\cdot})$
is a Markov process with the state space
![]() $\mathcal{M}^{(n)} \subset \mathcal{M}$
. Let us also consider a centered version of the process. Fix a number
$\mathcal{M}^{(n)} \subset \mathcal{M}$
. Let us also consider a centered version of the process. Fix a number
![]() $\nu \in (0,1)$
, and let
$\nu \in (0,1)$
, and let
![]() $\mathring{g}_x = g_{x+q_{\nu}(g)}, \,x \in \mathbb{R}.$
That is,
$\mathring{g}_x = g_{x+q_{\nu}(g)}, \,x \in \mathbb{R}.$
That is,
![]() $\mathring{g}$
is a version of g that is centered at its
$\mathring{g}$
is a version of g that is centered at its
![]() $\nu$
th quantile. Then
$\nu$
th quantile. Then
![]() $\mathring{f} {}^n(t)$
—the centered version of
$\mathring{f} {}^n(t)$
—the centered version of
![]() $f^n(t)$
—is also a Markov process, with state space
$f^n(t)$
—is also a Markov process, with state space
![]() $\mathring{\mathcal{M}} {}^{(n)} = \mathcal{M}^{(n)} \cap \mathring{\mathcal{M}}$
. This process is regenerative, with the regenerations occurring at time points when all particles ‘collapse’ to one location. A regeneration cycle has finite mean; indeed, for any time interval of a fixed length
$\mathring{\mathcal{M}} {}^{(n)} = \mathcal{M}^{(n)} \cap \mathring{\mathcal{M}}$
. This process is regenerative, with the regenerations occurring at time points when all particles ‘collapse’ to one location. A regeneration cycle has finite mean; indeed, for any time interval of a fixed length
![]() $\varepsilon>0$
, with probability at least some
$\varepsilon>0$
, with probability at least some
![]() $\delta=\delta(\varepsilon,n)>0$
, at the end of the interval all particles will be at a single location. Therefore the process is positive recurrent, with unique stationary distribution. Denote by
$\delta=\delta(\varepsilon,n)>0$
, at the end of the interval all particles will be at a single location. Therefore the process is positive recurrent, with unique stationary distribution. Denote by
![]() $\mathring{f} {}^n(\infty)$
a random element with distribution equal to the stationary distribution of
$\mathring{f} {}^n(\infty)$
a random element with distribution equal to the stationary distribution of
![]() $\mathring{f} {}^n({\cdot})$
.
$\mathring{f} {}^n({\cdot})$
.
Consider a version
![]() $f^n({\cdot})$
of the system process, such that the centered process
$f^n({\cdot})$
of the system process, such that the centered process
![]() $\mathring{f} {}^n({\cdot})$
is stationary. Specifically, consider the process
$\mathring{f} {}^n({\cdot})$
is stationary. Specifically, consider the process
![]() $f^n({\cdot})$
with
$f^n({\cdot})$
with
![]() $f^n(0)$
equal in distribution to
$f^n(0)$
equal in distribution to
![]() $\mathring{f} {}^n(\infty)$
. Then, for each n, the steady-state average speed
$\mathring{f} {}^n(\infty)$
. Then, for each n, the steady-state average speed
![]() $v_n$
of the particle system is finite and given by
$v_n$
of the particle system is finite and given by
where
![]() $\beta\in (0,1)$
and
$\beta\in (0,1)$
and
![]() $t>0$
can be chosen arbitrarily. Also,
$t>0$
can be chosen arbitrarily. Also,
![]() $v_n$
is the steady-state average speed of the center of mass, i.e. of the mean of the distribution
$v_n$
is the steady-state average speed of the center of mass, i.e. of the mean of the distribution
![]() $f^n(t)$
:
$f^n(t)$
:
Given the regenerative structure of the (centered) process, the steady-state speed
![]() $v_n$
can also be defined in terms of probability-one convergence, regardless of the initial state. In particular, for any initial state of the system,
$v_n$
can also be defined in terms of probability-one convergence, regardless of the initial state. In particular, for any initial state of the system,
where
![]() $D^n(t)$
is the location of the leading (rightmost) particle.
$D^n(t)$
is the location of the leading (rightmost) particle.
We remark that, trivially,
![]() $\lambda=0$
implies
$\lambda=0$
implies
![]() $v_n=0$
, because then, with probability one, all particles will end up at a single location and will stop moving after that. Therefore,
$v_n=0$
, because then, with probability one, all particles will end up at a single location and will stop moving after that. Therefore,
![]() $v_n > 0$
if and only if
$v_n > 0$
if and only if
![]() $\lambda>0$
, and we have the trivial lower bound
$\lambda>0$
, and we have the trivial lower bound
![]() $v_n \ge \lambda$
for any n.
$v_n \ge \lambda$
for any n.
Recall that we assumed
![]() $\mu=1$
. If we do need expressions for a case when
$\mu=1$
. If we do need expressions for a case when
![]() $\mu\ne 1$
, they are obtained from the corresponding expressions for the
$\mu\ne 1$
, they are obtained from the corresponding expressions for the
![]() $\mu=1$
case. For example, if
$\mu=1$
case. For example, if
![]() $v_n=v_n(\lambda,\mu)$
is the steady-state speed as a function of
$v_n=v_n(\lambda,\mu)$
is the steady-state speed as a function of
![]() $\lambda$
and
$\lambda$
and
![]() $\mu>0$
, then
$\mu>0$
, then
![]() $v_n(\lambda,\mu) = \mu v_n(\lambda/\mu,1)$
.
$v_n(\lambda,\mu) = \mu v_n(\lambda/\mu,1)$
.
4. Monotonicity properties
The order relation (stochastic dominance)
![]() $g^{(1)} \preceq g^{(2)}$
between two distributions
$g^{(1)} \preceq g^{(2)}$
between two distributions
![]() $g^{(1)}, g^{(2)} \in \mathcal{M}$
means
$g^{(1)}, g^{(2)} \in \mathcal{M}$
means
![]() $g^{(1)}_x \ge g^{(2)}_x, \,\forall x$
.
$g^{(1)}_x \ge g^{(2)}_x, \,\forall x$
.
The process
![]() $f^n({\cdot})$
possesses some simple monotonicity properties. If we have two versions of this process
$f^n({\cdot})$
possesses some simple monotonicity properties. If we have two versions of this process
![]() $f^n({\cdot})$
, labeled
$f^n({\cdot})$
, labeled
![]() $f^{n,(1)}({\cdot})$
and
$f^{n,(1)}({\cdot})$
and
![]() $f^{n,(2)}({\cdot})$
, with fixed initial conditions
$f^{n,(2)}({\cdot})$
, with fixed initial conditions
![]() $f^{n,(1)}(0) \preceq f^{n,(2)}(0)$
, then these two processes can be coupled (constructed on a common probability space) so that
$f^{n,(1)}(0) \preceq f^{n,(2)}(0)$
, then these two processes can be coupled (constructed on a common probability space) so that
![]() $f^{n,(1)}(t) \preceq f^{n,(2)}(t)$
at all times
$f^{n,(1)}(t) \preceq f^{n,(2)}(t)$
at all times
![]() $t\ge 0$
. Indeed, it suffices to set a one-to-one correspondence between particles in the two systems, such that each particle in the second system in initially ahead of the corresponding particle in the first system, and consider a probability space such that each pair of corresponding particles has the same realizations of time instants and sizes of the independent jumps, as well as the same realizations of the time instants and ‘targets’ of the synchronization jumps. Then, clearly, each particle in the second system will remain ahead of its counterpart in the first system at all times.
$t\ge 0$
. Indeed, it suffices to set a one-to-one correspondence between particles in the two systems, such that each particle in the second system in initially ahead of the corresponding particle in the first system, and consider a probability space such that each pair of corresponding particles has the same realizations of time instants and sizes of the independent jumps, as well as the same realizations of the time instants and ‘targets’ of the synchronization jumps. Then, clearly, each particle in the second system will remain ahead of its counterpart in the first system at all times.
This property easily generalizes to the case when the second (‘larger’) process has a larger number of particles, i.e. when we compare
![]() $f^{n,(1)}({\cdot})$
and
$f^{n,(1)}({\cdot})$
and
![]() $f^{k,(2)}({\cdot})$
, where
$f^{k,(2)}({\cdot})$
, where
![]() $n \le k$
. In this case, we will use the order relation
$n \le k$
. In this case, we will use the order relation
![]() $f^{n,(1)}(t) \preceq_l f^{k,(2)}(t)$
, which denotes the situation when
$f^{n,(1)}(t) \preceq_l f^{k,(2)}(t)$
, which denotes the situation when
![]() $f^{n,(1)}(t) \preceq f^{n(k),(2)}(t)$
, where
$f^{n,(1)}(t) \preceq f^{n(k),(2)}(t)$
, where
![]() $f^{n(k),(2)}(t)$
is the empirical distribution of the leading n particles of the state
$f^{n(k),(2)}(t)$
is the empirical distribution of the leading n particles of the state
![]() $f^{k,(2)}({\cdot})$
. Again, if
$f^{k,(2)}({\cdot})$
. Again, if
![]() $f^{n,(1)}(0) \preceq_l f^{k,(2)}(0)$
, then the processes can be coupled so that
$f^{n,(1)}(0) \preceq_l f^{k,(2)}(0)$
, then the processes can be coupled so that
![]() $f^{n,(1)}(t) \preceq_l f^{k,(2)}(t)$
prevails at all times. This extension has been used in the literature in different contexts (cf. the proof of Theorem 2.3(4) in [Reference Groisman, Jonckheere and Martínez13], and references therein), but is also easy to see directly. Indeed, the synchronization jumps can equivalently be defined as follows: a particle gets a ‘synchronization urge’ as a Poisson process of rate
$f^{n,(1)}(t) \preceq_l f^{k,(2)}(t)$
prevails at all times. This extension has been used in the literature in different contexts (cf. the proof of Theorem 2.3(4) in [Reference Groisman, Jonckheere and Martínez13], and references therein), but is also easy to see directly. Indeed, the synchronization jumps can equivalently be defined as follows: a particle gets a ‘synchronization urge’ as a Poisson process of rate
![]() $\mu$
(rescaled to 1), and it relocates another particle, chosen uniformly at random, to its own location if the chosen particle happens to be behind it. Given this interpretation, the coupling construction is straightforward.
$\mu$
(rescaled to 1), and it relocates another particle, chosen uniformly at random, to its own location if the chosen particle happens to be behind it. Given this interpretation, the coupling construction is straightforward.
Since the process is such that (a) for any initial state,
![]() $v_n = \lim_{t\to\infty} D^n(t)/t$
almost surely, where
$v_n = \lim_{t\to\infty} D^n(t)/t$
almost surely, where
![]() $D^n(t)$
is the location of the leading particle at time t, and (b) monotonicity with respect to
$D^n(t)$
is the location of the leading particle at time t, and (b) monotonicity with respect to
![]() $\preceq_l$
holds, we see that the steady-state speed
$\preceq_l$
holds, we see that the steady-state speed
![]() $v_n$
is non-decreasing in n:
$v_n$
is non-decreasing in n:
(Again, this property was used in the proof of Theorem 2.3(4) in [Reference Groisman, Jonckheere and Martínez13] for a different system, but it obviously holds for any system satisfying (a) and (b).)
The monotonicity with respect to
![]() $\preceq$
(and, more generally,
$\preceq$
(and, more generally,
![]() $\preceq_l$
) easily generalizes further in several directions. For example, it still holds if the ‘larger’ process
$\preceq_l$
) easily generalizes further in several directions. For example, it still holds if the ‘larger’ process
![]() $f^{k,(2)}({\cdot})$
has larger parameter
$f^{k,(2)}({\cdot})$
has larger parameter
![]() $\lambda$
, or if it is ‘helped’ by a left boundary (which can be static or moving in any way), or if the ‘smaller’ process
$\lambda$
, or if it is ‘helped’ by a left boundary (which can be static or moving in any way), or if the ‘smaller’ process
![]() $f^{n,(1)}({\cdot})$
is ‘impeded’ by a right boundary (which can be static or moving in any way), etc. We will not give formal statements for all these generalizations, and we will refer to the monotonicity properties described in this section simply as monotonicity.
$f^{n,(1)}({\cdot})$
is ‘impeded’ by a right boundary (which can be static or moving in any way), etc. We will not give formal statements for all these generalizations, and we will refer to the monotonicity properties described in this section simply as monotonicity.
5. Mean-field limits
In this section we state our results on the convergence to and characterization of MFLs. The results are for the original system, the system with fixed right boundary (which is primarily a tool for the analysis of the original system), and the two systems with moving right and left boundaries. We will use the same notation
![]() $f^n({\cdot})$
and
$f^n({\cdot})$
and
![]() $f({\cdot})$
for the process and an MFL, respectively, for each of the four systems. It should be clear that they do depend on the system, and when we use them later in the paper it will be clear from the context which system they refer to.
$f({\cdot})$
for the process and an MFL, respectively, for each of the four systems. It should be clear that they do depend on the system, and when we use them later in the paper it will be clear from the context which system they refer to.
5.1. Original system
The following definition of a mean-field model describes what it is natural to expect an MFL to be. Theorem 1 then shows that MFLs this definition.
Definition 1. A function
![]() $f_x(t), \,x\in \mathbb{R}, \,t\in \mathbb{R}_+,$
will be called a mean-field model (MFM) if it satisfies the following conditions:
$f_x(t), \,x\in \mathbb{R}, \,t\in \mathbb{R}_+,$
will be called a mean-field model (MFM) if it satisfies the following conditions:
-
(a) For any t,
 $f(t) = (f_x(t), x\in \mathbb{R}) \in \mathcal{M}$
.
$f(t) = (f_x(t), x\in \mathbb{R}) \in \mathcal{M}$
. -
(b) For any x,
 $f_x(t)$
is non-increasing and
$f_x(t)$
is non-increasing and
 $(\lambda+1)$
-Lipschitz in t.
$(\lambda+1)$
-Lipschitz in t. -
(c) For any x, for any t where the partial derivative
 $(\partial/\partial t) f_x(t)$
exists (which is almost all t with respect to the Lebesgue measure, by the Lipschitz property), the equation (5.1)holds.
$(\partial/\partial t) f_x(t)$
exists (which is almost all t with respect to the Lebesgue measure, by the Lipschitz property), the equation (5.1)holds. \begin{equation}\frac{\partial}{\partial t} f_x(t) = -\lambda \int_{-\infty}^x d_y f_y(t) (1-J(x-y)) - f_x(t) (1-f_x(t)).\end{equation}
\begin{equation}\frac{\partial}{\partial t} f_x(t) = -\lambda \int_{-\infty}^x d_y f_y(t) (1-J(x-y)) - f_x(t) (1-f_x(t)).\end{equation}
Denote by
![]() $L^{(n)}$
the generator of the process
$L^{(n)}$
the generator of the process
![]() $f^n({\cdot})$
. For any
$f^n({\cdot})$
. For any
![]() $h\in\mathcal{C}_b$
, the function
$h\in\mathcal{C}_b$
, the function
![]() $f^n h$
of an element
$f^n h$
of an element
![]() $f^n \in \mathcal{M}^{(n)}$
is within the domain of
$f^n \in \mathcal{M}^{(n)}$
is within the domain of
![]() $L^{(n)}$
(where we use the fact that each function in
$L^{(n)}$
(where we use the fact that each function in
![]() $\mathcal{C}_b$
is constant outside a closed interval), and
$\mathcal{C}_b$
is constant outside a closed interval), and
where the expectation is over the distribution of the random jump size Z. We also formally define the ‘limit’ L of
![]() $L^{(n)}$
(for elements
$L^{(n)}$
(for elements
![]() $f \in \mathcal{M}$
) as
$f \in \mathcal{M}$
) as
Theorem 1. Suppose
![]() $f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
$f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
![]() $\{f^n(0)\}$
is a deterministic sequence of elements
$\{f^n(0)\}$
is a deterministic sequence of elements
![]() $f^n(0) \in \mathcal{M}^{(n)}$
, and
$f^n(0) \in \mathcal{M}^{(n)}$
, and
![]() $f(0) \in \mathcal{M}$
. Then
$f(0) \in \mathcal{M}$
. Then
![]() $f^n({\cdot}) \Rightarrow f({\cdot})$
in
$f^n({\cdot}) \Rightarrow f({\cdot})$
in
![]() $D([0,\infty), \mathcal{M})$
, where
$D([0,\infty), \mathcal{M})$
, where
![]() $f({\cdot}) \in D([0,\infty), \mathcal{M})$
is deterministic and uniquely determined by f(0). Moreover,
$f({\cdot}) \in D([0,\infty), \mathcal{M})$
is deterministic and uniquely determined by f(0). Moreover,
![]() $f({\cdot})$
is a continuous element of
$f({\cdot})$
is a continuous element of
![]() $D([0,\infty), \mathcal{M})$
and satisfies
$D([0,\infty), \mathcal{M})$
and satisfies
The trajectory
![]() $f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, the MFL
$f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, the MFL
![]() $f({\cdot})$
is the unique MFM (see Definition 1) with initial state f(0).
$f({\cdot})$
is the unique MFM (see Definition 1) with initial state f(0).
The proof of Theorem 1 is in Section 13.
The MFL
![]() $f({\cdot})$
with initial state
$f({\cdot})$
with initial state
![]() $f(0)=\chi$
(i.e., the Dirac distribution concentrated at a single point 0) will be called the benchmark MFL (BMFL).
$f(0)=\chi$
(i.e., the Dirac distribution concentrated at a single point 0) will be called the benchmark MFL (BMFL).
5.2. System with fixed right boundary
As an intermediate step towards the proof of Theorem 1, we will prove a special case of it, Theorem 2 below, which applies to the system with fixed right boundary, defined as follows.
Note that, for any fixed B, the evolution of
![]() $f_x^n({\cdot}), x \in ({-}\infty, B)$
in our original system is independent of the actual locations and/or evolution of particles in
$f_x^n({\cdot}), x \in ({-}\infty, B)$
in our original system is independent of the actual locations and/or evolution of particles in
![]() $[B, \infty)$
. Therefore, if we are only interested in the evolution of
$[B, \infty)$
. Therefore, if we are only interested in the evolution of
![]() $f_x^n({\cdot}), x \in ({-}\infty, B)$
, we may as well assume that any particle in
$f_x^n({\cdot}), x \in ({-}\infty, B)$
, we may as well assume that any particle in
![]() $[B, \infty)$
is located exactly at B (that is,
$[B, \infty)$
is located exactly at B (that is,
![]() $f_B^n(t)=1$
at all times). In other words, we can assume that there is a fixed right boundary point B, and any particle which ‘tries to jump over B’ lands (absorbed) at exactly B. This is the modified system (with fixed right boundary) that we consider here. We see that the process
$f_B^n(t)=1$
at all times). In other words, we can assume that there is a fixed right boundary point B, and any particle which ‘tries to jump over B’ lands (absorbed) at exactly B. This is the modified system (with fixed right boundary) that we consider here. We see that the process
![]() $f^n({\cdot})$
for this system is a projection of the original process—it is such that
$f^n({\cdot})$
for this system is a projection of the original process—it is such that
![]() $f^n(t) \in \mathcal{M}^B \doteq \{g \in \mathcal{M} \,|\, g_B=1\}$
for all t.
$f^n(t) \in \mathcal{M}^B \doteq \{g \in \mathcal{M} \,|\, g_B=1\}$
for all t.
Denote by
![]() $L^{(n),B}$
the generator of the process
$L^{(n),B}$
the generator of the process
![]() $f^n({\cdot})$
for this system. For any
$f^n({\cdot})$
for this system. For any
![]() $h\in\mathcal{C}_b$
, the function
$h\in\mathcal{C}_b$
, the function
![]() $f^n h$
of an element
$f^n h$
of an element
![]() $f^n \in \mathcal{M}^{(n)} \cap \mathcal{M}^B$
is within the domain of
$f^n \in \mathcal{M}^{(n)} \cap \mathcal{M}^B$
is within the domain of
![]() $L^{(n),B}$
, and
$L^{(n),B}$
, and
where the expectation is over the distribution of the random jump size Z. We also formally define the ‘limit’
![]() $L^{B}$
of
$L^{B}$
of
![]() $L^{(n),B}$
(for elements
$L^{(n),B}$
(for elements
![]() $f \in \mathcal{M} \cap \mathcal{M}^B$
) as
$f \in \mathcal{M} \cap \mathcal{M}^B$
) as
Observe the following. For a fixed
![]() $h\in\mathcal{C}_b$
, if B is large enough so that h(x) is constant for all
$h\in\mathcal{C}_b$
, if B is large enough so that h(x) is constant for all
![]() $x \ge B$
, then
$x \ge B$
, then
![]() $L^{(n),B} [f^n h]= L^{(n)} [f^n h]$
and
$L^{(n),B} [f^n h]= L^{(n)} [f^n h]$
and
![]() $L^{B} [f^n h]= L [f^n h]$
, where
$L^{B} [f^n h]= L [f^n h]$
, where
![]() $L^{(n)}$
and L are the operators we defined for the original system.
$L^{(n)}$
and L are the operators we defined for the original system.
Theorem 2. Suppose
![]() $f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
$f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
![]() $\{f^n(0)\}$
is a deterministic sequence of elements
$\{f^n(0)\}$
is a deterministic sequence of elements
![]() $f^n(0) \in \mathcal{M}^{(n)} \cap \mathcal{M}^B$
, and
$f^n(0) \in \mathcal{M}^{(n)} \cap \mathcal{M}^B$
, and
![]() $f(0) \in \mathcal{M}^B$
. Then
$f(0) \in \mathcal{M}^B$
. Then
![]() $f^n({\cdot}) \Rightarrow f({\cdot})$
in
$f^n({\cdot}) \Rightarrow f({\cdot})$
in
![]() $D([0,\infty), \mathcal{M}^B)$
, where
$D([0,\infty), \mathcal{M}^B)$
, where
![]() $f({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
is deterministic and uniquely determined by f(0). Moreover,
$f({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
is deterministic and uniquely determined by f(0). Moreover,
![]() $f({\cdot})$
is a continuous element of
$f({\cdot})$
is a continuous element of
![]() $D([0,\infty), \mathcal{M}^B)$
which satisfies
$D([0,\infty), \mathcal{M}^B)$
which satisfies
This trajectory
![]() $f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, the MFL
$f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, the MFL
![]() $f({\cdot})$
is the unique MFM with initial state f(0); the MFM here is defined as in Definition 1 except that (5.1) holds for
$f({\cdot})$
is the unique MFM with initial state f(0); the MFM here is defined as in Definition 1 except that (5.1) holds for
![]() $x < B$
, and
$x < B$
, and
![]() $f_x(t) \equiv 1$
for
$f_x(t) \equiv 1$
for
![]() $x\ge B$
and all t.
$x\ge B$
and all t.
5.3. System with moving right boundary
Consider now the system with the right boundary point B moving to the right at constant speed
![]() $v>0$
, i.e.
$v>0$
, i.e.
![]() $B=B_0+vt$
for some constant
$B=B_0+vt$
for some constant
![]() $B_0$
. Just as in the system with fixed right boundary, any particle which ‘tries to jump over the boundary’ lands exactly at its current location. However, particles landing at the right boundary are not ‘absorbed’ in it, as the boundary keeps moving right while the particles do not move until they jump again. If B is the boundary location at time t, then the state
$B_0$
. Just as in the system with fixed right boundary, any particle which ‘tries to jump over the boundary’ lands exactly at its current location. However, particles landing at the right boundary are not ‘absorbed’ in it, as the boundary keeps moving right while the particles do not move until they jump again. If B is the boundary location at time t, then the state
![]() $f^n(t) \in \mathcal{M}^B$
. Formally speaking, the state of the Markov process has an additional component corresponding to the real number B; somewhat abusing notation, we will not include this component in the state descriptor.
$f^n(t) \in \mathcal{M}^B$
. Formally speaking, the state of the Markov process has an additional component corresponding to the real number B; somewhat abusing notation, we will not include this component in the state descriptor.
It is important to note that the process with moving right boundary is not a projection of the original process.
Denote by
![]() $L^{(n), \{r\}}$
the generator of the process
$L^{(n), \{r\}}$
the generator of the process
![]() $f^n({\cdot})$
for this system. For any
$f^n({\cdot})$
for this system. For any
![]() $h\in\mathcal{C}_b$
, the function
$h\in\mathcal{C}_b$
, the function
![]() $f^n h$
of an element
$f^n h$
of an element
![]() $f^n$
(or rather pair
$f^n$
(or rather pair
![]() $(f^n,B)$
) satisfying
$(f^n,B)$
) satisfying
![]() $f^n \in \mathcal{M}^{(n)} \cap \mathcal{M}^B$
is within the domain of
$f^n \in \mathcal{M}^{(n)} \cap \mathcal{M}^B$
is within the domain of
![]() $L^{(n), \{r\}}$
, and
$L^{(n), \{r\}}$
, and
where the expectation is over the distribution of the random jump size Z. We also formally define the ‘limit’
![]() $L^{\{r\}}$
of
$L^{\{r\}}$
of
![]() $L^{(n), \{r\}}$
(for pairs (f,B) satisfying
$L^{(n), \{r\}}$
(for pairs (f,B) satisfying
![]() $f \in \mathcal{M}^B$
) as
$f \in \mathcal{M}^B$
) as
The operators
![]() $L^{(n), \{r\}}$
and
$L^{(n), \{r\}}$
and
![]() $L^{\{r\}}$
are the same as the operators
$L^{\{r\}}$
are the same as the operators
![]() $L^{(n), B}$
and
$L^{(n), B}$
and
![]() $L^B$
, respectively, for the system with fixed right boundary at B. Here, however, B is part of the process state, rather than a fixed constant.
$L^B$
, respectively, for the system with fixed right boundary at B. Here, however, B is part of the process state, rather than a fixed constant.
Theorem 3. Let
![]() $v>0$
and
$v>0$
and
![]() $B_0$
be fixed, and recall that the boundary is given by
$B_0$
be fixed, and recall that the boundary is given by
![]() $B=B_0 +vt$
. Suppose
$B=B_0 +vt$
. Suppose
![]() $f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
$f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
![]() $\{f^n(0)\}$
is a deterministic sequence of elements
$\{f^n(0)\}$
is a deterministic sequence of elements
![]() $f^n(0) \in \mathcal{M}^{(n)} \cap \mathcal{M}^{B_0}$
, and
$f^n(0) \in \mathcal{M}^{(n)} \cap \mathcal{M}^{B_0}$
, and
![]() $f(0) \in \mathcal{M}^{B_0}$
. Then
$f(0) \in \mathcal{M}^{B_0}$
. Then
![]() $f^n({\cdot}) \Rightarrow f({\cdot})$
in
$f^n({\cdot}) \Rightarrow f({\cdot})$
in
![]() $D([0,\infty), \mathcal{M})$
, where
$D([0,\infty), \mathcal{M})$
, where
![]() $f({\cdot}) \in D([0,\infty), \mathcal{M})$
is deterministic and uniquely determined by f(0);
$f({\cdot}) \in D([0,\infty), \mathcal{M})$
is deterministic and uniquely determined by f(0);
![]() $f^n(t) \in \mathcal{M}^{(n)} \cap \mathcal{M}^{B}$
and
$f^n(t) \in \mathcal{M}^{(n)} \cap \mathcal{M}^{B}$
and
![]() $f(t) \in \mathcal{M}^{B}$
for all t. Moreover,
$f(t) \in \mathcal{M}^{B}$
for all t. Moreover,
![]() $f({\cdot})$
is a continuous element of
$f({\cdot})$
is a continuous element of
![]() $D([0,\infty), \mathcal{M})$
which satisfies
$D([0,\infty), \mathcal{M})$
which satisfies
This trajectory
![]() $f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, MFL
$f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, MFL
![]() $f({\cdot})$
is the unique MFM with initial state f(0); the MFM here is defined as in Definition 1 except that (5.1) holds for
$f({\cdot})$
is the unique MFM with initial state f(0); the MFM here is defined as in Definition 1 except that (5.1) holds for
![]() $x < B (=B_0 + vt)$
.
$x < B (=B_0 + vt)$
.
5.4. System with moving left boundary
Consider yet another modification of our original system, namely the system with left boundary A moving right at constant speed
![]() $v>0$
, i.e.
$v>0$
, i.e.
![]() $A=A_0+vt$
for some constant
$A=A_0+vt$
for some constant
![]() $A_0$
. In this system there are no particles to the left of A—as the boundary moves right it ‘drags forward’ any particle that it encounters, and each such particle stays at the (moving) boundary until it jumps forward. The corresponding process is not a projection of our original process.
$A_0$
. In this system there are no particles to the left of A—as the boundary moves right it ‘drags forward’ any particle that it encounters, and each such particle stays at the (moving) boundary until it jumps forward. The corresponding process is not a projection of our original process.
By the definition of the process, there are no particles located to the left of the moving boundary A. However, for the purposes of analysis it will be convenient to adopt an equivalent view of the process which allows particles to be to the left of A. Specifically, assume that particles make synchronization jumps as in the original system, but when a particle located at y makes an independent jump, it first instantly moves to the point
![]() $y \vee A$
and then jumps. Clearly, this process is such that the evolution in time of
$y \vee A$
and then jumps. Clearly, this process is such that the evolution in time of
![]() $(f^n_x(t), x \ge A)$
is exactly the same as it would be if the moving left boundary dragged the particles that it encountered with it. So this is how we will define the process
$(f^n_x(t), x \ge A)$
is exactly the same as it would be if the moving left boundary dragged the particles that it encountered with it. So this is how we will define the process
![]() $f^n({\cdot})$
for this system. Then
$f^n({\cdot})$
for this system. Then
![]() $f^n(t) \in \mathcal{M}^{(n)}$
for all t, and the boundary location A is implicitly a part of the definition of the process.
$f^n(t) \in \mathcal{M}^{(n)}$
for all t, and the boundary location A is implicitly a part of the definition of the process.
Denote by
![]() $L^{(n), \{l\}}$
the generator of the process
$L^{(n), \{l\}}$
the generator of the process
![]() $f^n({\cdot})$
. For any
$f^n({\cdot})$
. For any
![]() $h\in\mathcal{C}_b$
, the function
$h\in\mathcal{C}_b$
, the function
![]() $f^n h$
of an element
$f^n h$
of an element
![]() $f^n$
(or rather pair
$f^n$
(or rather pair
![]() $(f^n,A)$
) satisfying
$(f^n,A)$
) satisfying
![]() $f^n \in \mathcal{M}^{(n)}$
is within the domain of
$f^n \in \mathcal{M}^{(n)}$
is within the domain of
![]() $L^{(n), \{r\}}$
, and
$L^{(n), \{r\}}$
, and
where the expectation is over the distribution of the random jump size Z. We also formally define the ‘limit’
![]() $L^{\{l\}}$
of
$L^{\{l\}}$
of
![]() $L^{(n), \{l\}}$
(for pairs (f,A) with
$L^{(n), \{l\}}$
(for pairs (f,A) with
![]() $f \in \mathcal{M}$
) as
$f \in \mathcal{M}$
) as
Theorem 4. Let
![]() $v>0$
and
$v>0$
and
![]() $A_0$
be fixed, and recall that the boundary is given by
$A_0$
be fixed, and recall that the boundary is given by
![]() $A=A_0 +vt$
. Suppose
$A=A_0 +vt$
. Suppose
![]() $f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
$f^n(0) \stackrel{w}{\rightarrow} f(0)$
, where
![]() $\{f^n(0)\}$
is a deterministic sequence of elements
$\{f^n(0)\}$
is a deterministic sequence of elements
![]() $f^n(0) \in \mathcal{M}^{(n)}$
, and
$f^n(0) \in \mathcal{M}^{(n)}$
, and
![]() $f(0) \in \mathcal{M}$
. Then
$f(0) \in \mathcal{M}$
. Then
![]() $f^n({\cdot}) \Rightarrow f({\cdot})$
in
$f^n({\cdot}) \Rightarrow f({\cdot})$
in
![]() $D([0,\infty), \mathcal{M})$
, where
$D([0,\infty), \mathcal{M})$
, where
![]() $f({\cdot}) \in D([0,\infty), \mathcal{M})$
is deterministic and uniquely determined by f(0). Moreover,
$f({\cdot}) \in D([0,\infty), \mathcal{M})$
is deterministic and uniquely determined by f(0). Moreover,
![]() $f({\cdot})$
is a continuous element of
$f({\cdot})$
is a continuous element of
![]() $D([0,\infty), \mathcal{M})$
which satisfies
$D([0,\infty), \mathcal{M})$
which satisfies
This trajectory
![]() $f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, MFL
$f({\cdot})$
is called the mean-field limit (MFL) with initial state f(0). Furthermore, MFL
![]() $f({\cdot})$
is the unique MFM with initial state f(0); the MFM here is defined as in Definition 1 except that (5.1) is replaced by
$f({\cdot})$
is the unique MFM with initial state f(0); the MFM here is defined as in Definition 1 except that (5.1) is replaced by
5.5. Monotonicity of MFLs
The monotonicity properties described in Section 4, as well as the uniqueness of the MFL for each initial state, imply the following monotonicity property of MFLs.
Lemma 1. For two MFLs
![]() $f^{(1)}({\cdot})$
and
$f^{(1)}({\cdot})$
and
![]() $f^{(2)}({\cdot})$
,
$f^{(2)}({\cdot})$
,
![]() $f^{(1)}(0) \preceq f^{(2)}(0)$
implies
$f^{(1)}(0) \preceq f^{(2)}(0)$
implies
![]() $f^{(1)}(t) \preceq f^{(2)}(t)$
for all
$f^{(1)}(t) \preceq f^{(2)}(t)$
for all
![]() $t\ge 0$
.
$t\ge 0$
.
Just as the monotonicity properties of the process continue to hold for various generalizations (see Section 4), Lemma 1 holds under those generalizations as well.
6. MFLs that are traveling waves
An MFL (MFM)
![]() $f({\cdot})$
for our original system is a traveling wave if
$f({\cdot})$
for our original system is a traveling wave if
![]() $f_x(t) =\phi_{x-vt}$
for some speed
$f_x(t) =\phi_{x-vt}$
for some speed
![]() $v> 0$
and some
$v> 0$
and some
![]() $\phi = (\phi_x, x \in \mathbb{R}) \in \mathcal{M}$
, in which case we call
$\phi = (\phi_x, x \in \mathbb{R}) \in \mathcal{M}$
, in which case we call
![]() $\phi$
a traveling-wave shape (TWS). Substituting
$\phi$
a traveling-wave shape (TWS). Substituting
![]() $f_x(t) =\phi_{x-vt}$
into (5.1), we can easily see that a TWS, if it exists, must satisfy
$f_x(t) =\phi_{x-vt}$
into (5.1), we can easily see that a TWS, if it exists, must satisfy
for each x, and in fact the derivative
![]() $\phi^{\prime}_x$
must be continuous in x.
$\phi^{\prime}_x$
must be continuous in x.
Since a traveling wave is an MFL (which is a limit of particle system dynamics), we see that if a TWS with speed v exists, then necessarily
![]() $v \ge \lambda$
.
$v \ge \lambda$
.
In the special case when
![]() $\lambda=0$
, the integro-differential equation (6.1) becomes the logistic differential equation
$\lambda=0$
, the integro-differential equation (6.1) becomes the logistic differential equation
In this case, a unique (up to a shift) TWS does exist for every speed
![]() $v>0$
. This follows, for example, from [Reference Manita and Shcherbakov22, Proposition 5.1], but of course it is well known: the relevant solution to (6.2) is
$v>0$
. This follows, for example, from [Reference Manita and Shcherbakov22, Proposition 5.1], but of course it is well known: the relevant solution to (6.2) is
(There is no contradiction here with the fact that for any finite n,
![]() $\lambda=0$
implies that the steady-state speed
$\lambda=0$
implies that the steady-state speed
![]() $v_n=0$
. Traveling waves are MFLs, which means that we first take the
$v_n=0$
. Traveling waves are MFLs, which means that we first take the
![]() $n\to\infty$
limit and then look at the time-evolution of the limit. So, if the time interval [0,T] is fixed, n is very large, and the initial state
$n\to\infty$
limit and then look at the time-evolution of the limit. So, if the time interval [0,T] is fixed, n is very large, and the initial state
![]() $f^n(0)$
is close to
$f^n(0)$
is close to
![]() $\psi$
in (6.3), then the evolution of
$\psi$
in (6.3), then the evolution of
![]() $f_x^n(t)$
in [0,T] is close to the traveling wave
$f_x^n(t)$
in [0,T] is close to the traveling wave
![]() $\psi_{x-vt}$
moving at speed v. This does not contradict the fact that, eventually, all of the particles will assemble at the location of the leading particle and will stop moving, i.e.
$\psi_{x-vt}$
moving at speed v. This does not contradict the fact that, eventually, all of the particles will assemble at the location of the leading particle and will stop moving, i.e.
![]() $v_n=0$
.)
$v_n=0$
.)
In the special case of exponential jump size distribution,
![]() $J(x) =1- e^{-x}$
, for any
$J(x) =1- e^{-x}$
, for any
![]() $\lambda\ge 0$
, the integro-differential equation (6.1) becomes an ODE
$\lambda\ge 0$
, the integro-differential equation (6.1) becomes an ODE
Indeed, in this case (6.1) can be written as
from which, after differentiating in x, we obtain (6.4).
We will also consider MFLs that are traveling waves for the modified systems with moving right and left boundaries;
![]() $v>0$
is the speed of the boundary. Clearly, in a system with a boundary moving at speed v, the speed of any traveling wave is also v. For both systems, for a given boundary speed
$v>0$
is the speed of the boundary. Clearly, in a system with a boundary moving at speed v, the speed of any traveling wave is also v. For both systems, for a given boundary speed
![]() $v>0$
, an MFL
$v>0$
, an MFL
![]() $f({\cdot})$
is a traveling wave (of speed v) if
$f({\cdot})$
is a traveling wave (of speed v) if
![]() $f_x(t) =\phi_{x-vt}$
for some
$f_x(t) =\phi_{x-vt}$
for some
![]() $\phi = (\phi_x, x \in \mathbb{R}) \in \mathcal{M}$
, where
$\phi = (\phi_x, x \in \mathbb{R}) \in \mathcal{M}$
, where
![]() $\phi$
is called a TWS for the corresponding system; without loss of generality we can assume that the initial location of the boundary is 0.
$\phi$
is called a TWS for the corresponding system; without loss of generality we can assume that the initial location of the boundary is 0.
Substituting
![]() $f_x(t) =\phi_{x-vt}$
into (5.1), we see that a TWS
$f_x(t) =\phi_{x-vt}$
into (5.1), we see that a TWS
![]() $\phi$
for the system with moving right boundary, if it exists, must be continuous with
$\phi$
for the system with moving right boundary, if it exists, must be continuous with
![]() $\phi_0=1$
and must satisfy (6.1) for each
$\phi_0=1$
and must satisfy (6.1) for each
![]() $x<0$
; in fact, the derivative
$x<0$
; in fact, the derivative
![]() $\phi^{\prime}_x$
must be continuous in
$\phi^{\prime}_x$
must be continuous in
![]() $({-}\infty,0]$
(if at
$({-}\infty,0]$
(if at
![]() $x=0$
we consider the left derivative). In the special case of
$x=0$
we consider the left derivative). In the special case of
![]() $J(x) =1-e^{-x}$
, (6.1) reduces to (6.4).
$J(x) =1-e^{-x}$
, (6.1) reduces to (6.4).
Substituting
![]() $f_x(t) =\phi_{x-vt}$
into (5.7), we obtain that a TWS
$f_x(t) =\phi_{x-vt}$
into (5.7), we obtain that a TWS
![]() $\phi$
for the system with moving left boundary, if it exists, must be continuous for
$\phi$
for the system with moving left boundary, if it exists, must be continuous for
![]() $x\in [0,\infty)$
and must satisfy
$x\in [0,\infty)$
and must satisfy
for each
![]() $x>0$
; in fact, the derivative
$x>0$
; in fact, the derivative
![]() $\phi^{\prime}_x$
must be continuous in
$\phi^{\prime}_x$
must be continuous in
![]() $[0,\infty)$
(if at
$[0,\infty)$
(if at
![]() $x=0$
we consider the right derivative). Note that the initial condition
$x=0$
we consider the right derivative). Note that the initial condition
![]() $v \phi^{\prime}_0 = \lambda \phi_0 + \phi_0(1-\phi)$
must hold. In the special case of
$v \phi^{\prime}_0 = \lambda \phi_0 + \phi_0(1-\phi)$
must hold. In the special case of
![]() $J(x) =1-e^{-x}$
, (6.5) reduces to (6.4).
$J(x) =1-e^{-x}$
, (6.5) reduces to (6.4).
7. Definition of the critical speed
 $v_{**}$
via an MSSP
$v_{**}$
via an MSSP
In this section we formally define the critical value
![]() $v_{**}$
of the speed, which plays a central role in our results and analysis. Assume
$v_{**}$
of the speed, which plays a central role in our results and analysis. Assume
![]() $\lambda>0$
. Denote by
$\lambda>0$
. Denote by
![]() $L(s)= \int_0^\infty e^{-sx} dJ(x)$
the Laplace transform of the jump distribution
$L(s)= \int_0^\infty e^{-sx} dJ(x)$
the Laplace transform of the jump distribution
![]() $J({\cdot})$
. As a function of real s it is, of course, a convex non-negative non-increasing function. Denote by
$J({\cdot})$
. As a function of real s it is, of course, a convex non-negative non-increasing function. Denote by
![]() $\alpha$
the tail exponent of
$\alpha$
the tail exponent of
![]() $J({\cdot})$
:
$J({\cdot})$
:
Suppose
![]() $\alpha>0$
(with the case
$\alpha>0$
(with the case
![]() $\alpha=\infty$
allowed). Then
$\alpha=\infty$
allowed). Then
![]() $L(s) <+\infty$
for
$L(s) <+\infty$
for
![]() $s> - \alpha$
,
$s> - \alpha$
,
![]() $L(s) = +\infty$
for
$L(s) = +\infty$
for
![]() $s < - \alpha$
, and
$s < - \alpha$
, and
![]() $L(s) \uparrow L({-}\alpha)$
as
$L(s) \uparrow L({-}\alpha)$
as
![]() $s \downarrow -\alpha$
;
$s \downarrow -\alpha$
;
![]() $L({-}\alpha)$
may be finite or infinite, but it is necessarily infinite when
$L({-}\alpha)$
may be finite or infinite, but it is necessarily infinite when
![]() $\alpha=\infty$
.
$\alpha=\infty$
.
The following heuristic argument, leading to (7.3), is analogous to the one in, e.g., [Reference Brunet and Derrida6], where it is applied to the KPP equation (1.1). This heuristic argument serves as a motivation for the rigorous definition of the speed value
![]() $v_{**}$
. Assume that a TWS
$v_{**}$
. Assume that a TWS
![]() $\phi = (\phi_x, \,x\in \mathbb{R})$
with speed
$\phi = (\phi_x, \,x\in \mathbb{R})$
with speed
![]() $v>0$
exists, and that the front tail of
$v>0$
exists, and that the front tail of
![]() $\phi$
decays exponentially:
$\phi$
decays exponentially:
![]() $1-\phi_x \sim e^{-\zeta x}$
as
$1-\phi_x \sim e^{-\zeta x}$
as
![]() $x\to\infty$
, where
$x\to\infty$
, where
![]() $\zeta>0$
. Then, when x is large, Equation (6.1) ‘becomes’
$\zeta>0$
. Then, when x is large, Equation (6.1) ‘becomes’
In (7.2),
so we obtain the following dependence of the speed v on
![]() $\zeta>0$
:
$\zeta>0$
:
The relation (7.3), viewed formally, is a starting point for the following rigorous definitions and observations. The dependence
![]() $v(\zeta)$
is convex, because
$v(\zeta)$
is convex, because
![]() $(1/\zeta) [L({-}\zeta)-1]$
is the Laplace transform of function
$(1/\zeta) [L({-}\zeta)-1]$
is the Laplace transform of function
![]() $\bar J({\cdot})$
at the point
$\bar J({\cdot})$
at the point
![]() $s=-\zeta$
. Note also that
$s=-\zeta$
. Note also that
![]() $v(\zeta)\to +\infty$
as
$v(\zeta)\to +\infty$
as
![]() $\zeta\downarrow 0$
. It is easy to see that the minimum value
$\zeta\downarrow 0$
. It is easy to see that the minimum value
![]() $v_{**}$
of
$v_{**}$
of
![]() $v(\zeta)$
is attained at the unique positive finite value
$v(\zeta)$
is attained at the unique positive finite value
Because
![]() $\zeta_{**} \in (0,\alpha]$
and
$\zeta_{**} \in (0,\alpha]$
and
![]() $L({-}\zeta) > 1$
for
$L({-}\zeta) > 1$
for
![]() $\zeta>0$
, note from (7.3) that
$\zeta>0$
, note from (7.3) that
If
![]() $\zeta_{**} < \alpha$
, then it necessarily solves the equation
$\zeta_{**} < \alpha$
, then it necessarily solves the equation
and if
![]() $L({-}\alpha) =\infty$
, then necessarily
$L({-}\alpha) =\infty$
, then necessarily
![]() $\zeta_{**} < \alpha$
. Note for future reference that the inverse function to
$\zeta_{**} < \alpha$
. Note for future reference that the inverse function to
![]() $v(\zeta), \,0<\zeta \le \zeta_{**},$
is a continuous strictly decreasing convex function
$v(\zeta), \,0<\zeta \le \zeta_{**},$
is a continuous strictly decreasing convex function
![]() $\zeta(v), v_{**} \le v < \infty,$
with
$\zeta(v), v_{**} \le v < \infty,$
with
![]() $\zeta(v) \downarrow 0$
as
$\zeta(v) \downarrow 0$
as
![]() $v\uparrow\infty$
.
$v\uparrow\infty$
.
In the special case
![]() $\bar J(x) = e^{-x}$
, we have
$\bar J(x) = e^{-x}$
, we have
![]() $\alpha=1$
, (7.3) becomes
$\alpha=1$
, (7.3) becomes
and then
The inverse function
![]() $\zeta(v), v_{*} \le v < \infty,$
of the function
$\zeta(v), v_{*} \le v < \infty,$
of the function
![]() $v(\zeta), \,0<\zeta \le \zeta_{*},$
in this case is
$v(\zeta), \,0<\zeta \le \zeta_{*},$
in this case is
Recall that the above definition of
![]() $v_{**}$
assumes
$v_{**}$
assumes
![]() $\alpha>0$
. In view of (7.5), we adopt the convention that
$\alpha>0$
. In view of (7.5), we adopt the convention that
![]() $v_{**} = +\infty$
when
$v_{**} = +\infty$
when
![]() $\alpha=0$
. All results in this paper involving the critical speed
$\alpha=0$
. All results in this paper involving the critical speed
![]() $v_{**}$
are valid for the case when
$v_{**}$
are valid for the case when
![]() $\alpha=0$
and
$\alpha=0$
and
![]() $v_{**} = +\infty$
. They follow easily from the corresponding results for the case when
$v_{**} = +\infty$
. They follow easily from the corresponding results for the case when
![]() $\alpha > 0$
and
$\alpha > 0$
and
![]() $v_{**} < \infty$
, thanks to monotonicity (Section 4). Specifically, if
$v_{**} < \infty$
, thanks to monotonicity (Section 4). Specifically, if
![]() $\alpha=0$
, then we can compare the actual process to an auxiliary one with the jump size distribution slightly changed so that it is stochastically smaller, with an arbitrarily small positive tail exponent
$\alpha=0$
, then we can compare the actual process to an auxiliary one with the jump size distribution slightly changed so that it is stochastically smaller, with an arbitrarily small positive tail exponent
![]() $\alpha$
. The auxiliary process, which is stochastically dominated by the actual one, can have an arbitrarily large value of
$\alpha$
. The auxiliary process, which is stochastically dominated by the actual one, can have an arbitrarily large value of
![]() $v_{**}$
. Thus, the corresponding results for the actual process hold with
$v_{**}$
. Thus, the corresponding results for the actual process hold with
![]() $v_{**}=\infty$
.
$v_{**}=\infty$
.
8. Limit of steady-state speeds and the associated BRW
8.1. McKean-type characterization of the original system’s BMFL
Theorem 5 (presented in this section) and its proof are analogous to the corresponding result and its proof in [Reference McKean23], for the system in which the independent movement of each particle is a Brownian motion.
Denote by
![]() $W(t), \,t \ge 0,$
a single-particle independent-jump (Markov) process, starting at some point y at initial time
$W(t), \,t \ge 0,$
a single-particle independent-jump (Markov) process, starting at some point y at initial time
![]() $t=0$
. Specifically, W(t) is the location at time t of a particle that starts at 0 and makes independent and identically distributed jumps, distributed as
$t=0$
. Specifically, W(t) is the location at time t of a particle that starts at 0 and makes independent and identically distributed jumps, distributed as
![]() $J({\cdot})$
, at time points of a Poisson process of rate
$J({\cdot})$
, at time points of a Poisson process of rate
![]() $\lambda>0$
.
$\lambda>0$
.
Consider the following process, which we will call the associated (with our particle system) branching random walk (BRW). The process starts with a single particle, located initially at 0. Its location
![]() $W_1(t)$
evolves as a single-particle independent-jump process. Any particle present in the system generates a new particle in the same location (i.e. splits into two) according to a unit-rate Poisson process. Each newly created particle continues as a single-particle independent-jump process. We label particles in the order of their creation, so that at time t their locations are
$W_1(t)$
evolves as a single-particle independent-jump process. Any particle present in the system generates a new particle in the same location (i.e. splits into two) according to a unit-rate Poisson process. Each newly created particle continues as a single-particle independent-jump process. We label particles in the order of their creation, so that at time t their locations are
![]() $W_1(t), \ldots, W_{N(t)}(t)$
, where N(t) is the total number of particles. Let
$W_1(t), \ldots, W_{N(t)}(t)$
, where N(t) is the total number of particles. Let
![]() $D(t) \doteq \max_i W_i(t)$
be the location of the rightmost particle of the associated BRW.
$D(t) \doteq \max_i W_i(t)$
be the location of the rightmost particle of the associated BRW.
Theorem 5. The associated BRW is such that
where f(t) is the BMFL.
8.2. The value
 $v_{**}$
as the limiting average speed of the leading particle of the associated BRW
$v_{**}$
as the limiting average speed of the leading particle of the associated BRW
The following proposition can be obtained from a general result on the average speed of progress of a leading particle of a BRW in discrete time, namely Theorem 3 in [Reference Biggins3].
Proposition 1. Consider the associated BRW, starting with one particle. Let D(t) be the location of the leading particle at time t. Then
Indeed, the process can viewed as follows. Each particle already present in the process ‘waits’ for an independent, exponentially distributed time with mean
![]() $1/(1+\lambda)$
, and then either jumps forward (with probability
$1/(1+\lambda)$
, and then either jumps forward (with probability
![]() $\lambda/(1+\lambda)$
) or splits into two particles at the same location (with probability
$\lambda/(1+\lambda)$
) or splits into two particles at the same location (with probability
![]() $1/(1+\lambda)$
). Suppose we discretize time, with the time step being some small
$1/(1+\lambda)$
). Suppose we discretize time, with the time step being some small
![]() $\delta>0$
. We obtain a process ‘slower’ than the original one if we assume that the time
$\delta>0$
. We obtain a process ‘slower’ than the original one if we assume that the time
![]() $\tau$
a particle ‘waits’ until the next event is geometric, with
$\tau$
a particle ‘waits’ until the next event is geometric, with
![]() $\mathbb{P}\{\tau = j\delta\} = \varepsilon (1-\varepsilon)^{j-1}$
,
$\mathbb{P}\{\tau = j\delta\} = \varepsilon (1-\varepsilon)^{j-1}$
,
![]() $j=1,2,\ldots$
,
$j=1,2,\ldots$
,
![]() $\varepsilon=1-\exp({-}(1+\lambda)\delta)$
. The particles present at time
$\varepsilon=1-\exp({-}(1+\lambda)\delta)$
. The particles present at time
![]() $n\delta$
represent the nth generation of the particles. The process is such that, after each time step, a particle has either one descendant in the same location (with probability
$n\delta$
represent the nth generation of the particles. The process is such that, after each time step, a particle has either one descendant in the same location (with probability
![]() $1-\varepsilon$
), or two descendants in the same location (with probability
$1-\varepsilon$
), or two descendants in the same location (with probability
![]() $\varepsilon/(1+\lambda)$
), or one descendant located at the current particle location + Z. Theorem 3 in [Reference Biggins3] can be applied to this discrete-time process to obtain the leading particle’s average speed of progress, which is a lower bound on the speed of progress for the original process. To obtain a discrete-time process which is ‘faster’ than the original one, we assume that the time
$\varepsilon/(1+\lambda)$
), or one descendant located at the current particle location + Z. Theorem 3 in [Reference Biggins3] can be applied to this discrete-time process to obtain the leading particle’s average speed of progress, which is a lower bound on the speed of progress for the original process. To obtain a discrete-time process which is ‘faster’ than the original one, we assume that the time
![]() $\tau$
a particle ‘waits’ until the next event is geometric, with
$\tau$
a particle ‘waits’ until the next event is geometric, with
![]() $\mathbb{P}\{\tau = j\delta\} = \varepsilon (1-\varepsilon)^{j}$
,
$\mathbb{P}\{\tau = j\delta\} = \varepsilon (1-\varepsilon)^{j}$
,
![]() $j=0,1,2,\ldots$
. (A subtlety here is that
$j=0,1,2,\ldots$
. (A subtlety here is that
![]() $\tau=0$
with non-zero probability, so that the distribution of the set of descendants after one time step, i.e. after time
$\tau=0$
with non-zero probability, so that the distribution of the set of descendants after one time step, i.e. after time
![]() $\delta$
, has to account for that.) Applying Theorem 3 in [Reference Biggins3] to this discrete-time process, we obtain an upper bound on the leading particle’s average speed of progress for the original process. Letting
$\delta$
, has to account for that.) Applying Theorem 3 in [Reference Biggins3] to this discrete-time process, we obtain an upper bound on the leading particle’s average speed of progress for the original process. Letting
![]() $\delta\downarrow 0$
, we can check that both bounds converge to exactly
$\delta\downarrow 0$
, we can check that both bounds converge to exactly
![]() $v_{**}$
.
$v_{**}$
.
9. TWSs in the case of exponentially distributed independent jumps
Theorem 7. Consider the special case
![]() $J(x) =1-e^{-x}$
and recall the notation
$J(x) =1-e^{-x}$
and recall the notation
![]() $v_* = (1+\sqrt{\lambda})^2$
. Assume
$v_* = (1+\sqrt{\lambda})^2$
. Assume
![]() $\lambda>0$
. Then the following hold:
$\lambda>0$
. Then the following hold:
(i) A TWS
![]() $\phi$
for the original system exists if and only if
$\phi$
for the original system exists if and only if
![]() $v \ge v_*$
. If
$v \ge v_*$
. If
![]() $v>v_*$
, then
$v>v_*$
, then
where
![]() $\zeta(v)$
is defined in (7.8).
$\zeta(v)$
is defined in (7.8).
(ii) For any
![]() $v > v_*$
there exists a TWS
$v > v_*$
there exists a TWS
![]() $\phi$
for the system with moving left boundary at speed v, and it is such that (9.1) holds.
$\phi$
for the system with moving left boundary at speed v, and it is such that (9.1) holds.
(iii) For any
![]() $v < v_*$
there exists a unique TWS
$v < v_*$
there exists a unique TWS
![]() $\phi$
for the system with moving right boundary at speed v.
$\phi$
for the system with moving right boundary at speed v.
10. MFL speed results
The following is a natural and standard notion of the average speed of a given MFL. We say that the average speed of an MFL f(t) with a given initial state
![]() $f(0) \in \mathcal{M}$
is lower-bounded (upper-bounded) by v if, for any quantile
$f(0) \in \mathcal{M}$
is lower-bounded (upper-bounded) by v if, for any quantile
![]() $\nu \in (0,1)$
of f(t), its average speed of progress is lower-bounded (upper-bounded) by v; that is,
$\nu \in (0,1)$
of f(t), its average speed of progress is lower-bounded (upper-bounded) by v; that is,
An equivalent definition of a lower (upper) speed bound v is that for any
![]() $\varepsilon >0$
,
$\varepsilon >0$
,
The speed v is the average speed of an MFL if it is both a lower and an upper bound.
Clearly an MFL’s average speed depends on the initial state, and it can be arbitrarily large. (This follows from the existence of a traveling wave with
![]() $\lambda=0$
and arbitrarily large speed v.)
$\lambda=0$
and arbitrarily large speed v.)
As a corollary of Theorem 5 and Proposition 1 we obtain the following result.
Proposition 2. The average speed of the BMFL is
![]() $v_{**}$
.
$v_{**}$
.
Proposition 2 in turn is used to prove (in Section 19) the following theorem.
Theorem 8. The average speed of any MFL is lower-bounded by
![]() $v_{**}$
.
$v_{**}$
.
In cases when one can establish the existence of traveling waves, including traveling waves with moving boundaries—as we did in the case of exponential jump sizes—those traveling waves can be used as lower and/or upper bounds for MFLs to obtain more precise MFL speed bounds. Specifically, we can use the following fact, which is a corollary of Lemma 1.
Proposition 3. Consider an MFL
![]() $f({\cdot})$
. If there exists a traveling wave
$f({\cdot})$
. If there exists a traveling wave
![]() $\phi({\cdot})$
with speed v, and possibly with a lower (resp. upper) boundary with speed v, such that
$\phi({\cdot})$
with speed v, and possibly with a lower (resp. upper) boundary with speed v, such that
![]() $f(0) \preceq \phi(0)$
(resp.
$f(0) \preceq \phi(0)$
(resp.
![]() $\phi(0) \preceq f(0)$
), then
$\phi(0) \preceq f(0)$
), then
![]() $f(t) \preceq \phi(t)$
(resp.
$f(t) \preceq \phi(t)$
(resp.
![]() $\phi(t) \preceq f(t)$
) at all times, and consequently the MFL speed is lower-bounded (resp. upper-bounded) by v.
$\phi(t) \preceq f(t)$
) at all times, and consequently the MFL speed is lower-bounded (resp. upper-bounded) by v.
Theorem 9. Assume
![]() $J(x) = 1-e^{-x}$
.
$J(x) = 1-e^{-x}$
.
(i) The average speed of the BMFL is
![]() $v_*$
, and the average speed of any MFL is lower-bounded by
$v_*$
, and the average speed of any MFL is lower-bounded by
![]() $v_{*}$
.
$v_{*}$
.
(ii) If the right tail exponent of an MFL
![]() $f({\cdot})$
with initial state f(0) is lower-bounded by
$f({\cdot})$
with initial state f(0) is lower-bounded by
![]() $\zeta \le \zeta_*$
, i.e.
$\zeta \le \zeta_*$
, i.e.
![]() $\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta$
, then the MFL’s average speed is upper-bounded by
$\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta$
, then the MFL’s average speed is upper-bounded by
![]() $v(\zeta)$
. Consequently, if
$v(\zeta)$
. Consequently, if
![]() $\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta_*$
, then the MFL’s average speed is
$\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta_*$
, then the MFL’s average speed is
![]() $v_*$
.
$v_*$
.
(iii) If the right tail exponent of an MFL
![]() $f({\cdot})$
with initial state f(0) is upper-bounded by
$f({\cdot})$
with initial state f(0) is upper-bounded by
![]() $\zeta \le \zeta_*$
, i.e.
$\zeta \le \zeta_*$
, i.e.
![]() $\limsup_{x\to\infty} - \log (1-f_x(0))/x \le \zeta$
, then the MFL’s average speed is lower-bounded by
$\limsup_{x\to\infty} - \log (1-f_x(0))/x \le \zeta$
, then the MFL’s average speed is lower-bounded by
![]() $v(\zeta)$
.
$v(\zeta)$
.
The proof of Theorem 9 is in Section 20. This proof does not rely on Proposition 2, which in turn relies on the connection to the associated BRW and its properties, as described in Theorem 5 and Proposition 1. It relies only on Theorem 7 and Proposition 3. (This is why we include the statement (i) in Theorem 9, even though it is a special case of Proposition 2 and Theorem 8. We give an alternative proof of (i).)
The proof of Theorem 9 shows how MFL speed bounds can be obtained directly from the existence and properties of traveling waves. In our case these are given by Theorem 7. However, the proof is quite generic. For example, some of the MFL speed bounds for the KPP model under certain initial conditions, as obtained in [Reference Freidlin9, Reference Freidlin10, Reference Larson16, Reference Veretennikov27] via direct analysis or via Feynmann–Kac representations and large-deviations analysis, can be instead obtained in essentially the same way as our Theorem 9. Indeed, given the traveling-wave existence results for the KPP model [Reference Kolmogorov, Petrovskii and Piscounov15], it is straightforward to obtain an analogue of our Theorem 7, namely the existence of traveling waves with moving left and right boundaries for speeds larger and smaller, respectively, than the critical speed. Then an analogue of our Theorem 9 follows, with essentially the same proof.
11. Conjectures, simulation results, and discussion
11.1. Conjectures
We have proved that the limit of the steady-state speeds,
![]() $\lim_{n\to\infty} v_n = v_{**}$
, holds for our model with independent jump sizes having general distributions. However, we proved Theorem 7 and Theorem 9(ii)–(iii) only for exponential jumps. We conjecture that analogues of Theorem 7 and Theorem 9(ii)–(iii) in fact hold for generally distributed jump sizes as well. We also conjecture that stationary distributions of centered processes converge to the Dirac measure concentrated on a TWS. Formally, we put forward the following conjecture.
$\lim_{n\to\infty} v_n = v_{**}$
, holds for our model with independent jump sizes having general distributions. However, we proved Theorem 7 and Theorem 9(ii)–(iii) only for exponential jumps. We conjecture that analogues of Theorem 7 and Theorem 9(ii)–(iii) in fact hold for generally distributed jump sizes as well. We also conjecture that stationary distributions of centered processes converge to the Dirac measure concentrated on a TWS. Formally, we put forward the following conjecture.
Conjecture 1. Suppose the jump size distribution
![]() $J({\cdot})$
is such that
$J({\cdot})$
is such that
![]() $\alpha >0$
. Then the following hold:
$\alpha >0$
. Then the following hold:
(i) A unique TWS exists for any speed
![]() $v \ge v_{**}$
, and a TWS does not exist for speeds
$v \ge v_{**}$
, and a TWS does not exist for speeds
![]() $v< v_{**}$
.
$v< v_{**}$
.
(ii) If the right tail exponent of an MFL
![]() $f({\cdot})$
with initial state f(0) is lower-bounded by
$f({\cdot})$
with initial state f(0) is lower-bounded by
![]() $\zeta \le \zeta_{**}$
, i.e.
$\zeta \le \zeta_{**}$
, i.e.
![]() $\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta$
, then the MFL’s average speed is upper-bounded by
$\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta$
, then the MFL’s average speed is upper-bounded by
![]() $v(\zeta)$
. Consequently, if
$v(\zeta)$
. Consequently, if
![]() $\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta_{**}$
, then the MFL’s average speed is
$\liminf_{x\to\infty} - \log (1-f_x(0))/x \ge \zeta_{**}$
, then the MFL’s average speed is
![]() $v_{**}$
.
$v_{**}$
.
(iii) If the right tail exponent of an MFL
![]() $f({\cdot})$
with initial state f(0) is upper-bounded by
$f({\cdot})$
with initial state f(0) is upper-bounded by
![]() $\zeta \le \zeta_{**}$
, i.e.
$\zeta \le \zeta_{**}$
, i.e.
![]() $\limsup_{x\to\infty} - \log (1-f_x(0))/x \le \zeta$
, then the MFL’s average speed is lower-bounded by
$\limsup_{x\to\infty} - \log (1-f_x(0))/x \le \zeta$
, then the MFL’s average speed is lower-bounded by
![]() $v(\zeta)$
.
$v(\zeta)$
.
(iv) We have
![]() $\mathring{f} {}^n(\infty) \Rightarrow \phi^{**}$
, where
$\mathring{f} {}^n(\infty) \Rightarrow \phi^{**}$
, where
![]() $\phi^{**}$
is the TWS for the speed
$\phi^{**}$
is the TWS for the speed
![]() $v_{**}$
.
$v_{**}$
.
Proving Conjecture 1, or at least some parts of it, would be an interesting subject for future work.
11.2. Simulations and discussion
Before presenting our simulation results, we note that if the objective is to maximize the steady-state speed of progress of a large-scale system, then our Theorem 6 allows one to easily optimize the trade-off between
![]() $\lambda$
and
$\lambda$
and
![]() $\mu$
, if these quantities are chosen subject to some constraint(s). For example, one may want to optimize the trade-off between the levels of effort allocated to self-propulsion and synchronization, if both require the consumption of a common limited resource. Our simulations show good accuracy of the optimal setting based on Theorem 6.
$\mu$
, if these quantities are chosen subject to some constraint(s). For example, one may want to optimize the trade-off between the levels of effort allocated to self-propulsion and synchronization, if both require the consumption of a common limited resource. Our simulations show good accuracy of the optimal setting based on Theorem 6.
Tables 1 and 2 show steady-state speeds
![]() $v_n$
, obtained by simulation of a system with
$v_n$
, obtained by simulation of a system with
![]() $n=10000$
particles, under exponentially and uniformly (in [0, 2) distributed jump sizes, respectively. (For each simulation run, there are
$n=10000$
particles, under exponentially and uniformly (in [0, 2) distributed jump sizes, respectively. (For each simulation run, there are
![]() $400 \times n$
attempted jumps in total, i.e. 400 per particle. This corresponds to simulation time
$400 \times n$
attempted jumps in total, i.e. 400 per particle. This corresponds to simulation time
![]() $400 \times n / (\lambda+\mu)$
. The first half of the simulation run is a warm-up.) The tables also show the values of
$400 \times n / (\lambda+\mu)$
. The first half of the simulation run is a warm-up.) The tables also show the values of
![]() $v_{**}$
. (For the case of exponential jump sizes,
$v_{**}$
. (For the case of exponential jump sizes,
![]() $v_{**}= v_*=(\sqrt{\lambda} + \sqrt{\mu})^2$
.)
$v_{**}= v_*=(\sqrt{\lambda} + \sqrt{\mu})^2$
.)
Table 1. Exponential jump sizes,
![]() $n=10000$
,
$n=10000$
,
![]() $2\lambda+\mu=1$
. Steady-state speed
$2\lambda+\mu=1$
. Steady-state speed
![]() $v_n$
(simulated) and
$v_n$
(simulated) and
![]() $v_{**}=\lim_n v_n$
. (For exponential jump sizes,
$v_{**}=\lim_n v_n$
. (For exponential jump sizes,
![]() $v_{**} = (\sqrt{\lambda} + \sqrt{\mu})^2$
.) The pair
$v_{**} = (\sqrt{\lambda} + \sqrt{\mu})^2$
.) The pair
![]() $(\lambda_{opt}, \mu_{opt})$
maximizes
$(\lambda_{opt}, \mu_{opt})$
maximizes
![]() $v_{**}$
.
$v_{**}$
.

Table 2. Uniform[0, 2] jump sizes,
![]() $n=10000$
,
$n=10000$
,
![]() $2\lambda+\mu=1$
. Steady-state speed
$2\lambda+\mu=1$
. Steady-state speed
![]() $v_n$
(simulated) and
$v_n$
(simulated) and
![]() $v_{**}=\lim_n v_n$
. The pair
$v_{**}=\lim_n v_n$
. The pair
![]() $(\lambda_{opt}, \mu_{opt})$
maximizes
$(\lambda_{opt}, \mu_{opt})$
maximizes
![]() $v_{**}$
.
$v_{**}$
.

The results for exponential jump sizes are in Table 1. We see that the actual steady-state speed
![]() $v_n$
stays below
$v_n$
stays below
![]() $v_{**}$
, as we know it should. We also observe that, even for a relatively large number of particles (10000), the difference
$v_{**}$
, as we know it should. We also observe that, even for a relatively large number of particles (10000), the difference
![]() $v_{10000} - v_{**}$
is still significant. This is not unexpected, because the convergence
$v_{10000} - v_{**}$
is still significant. This is not unexpected, because the convergence
![]() $v_n \uparrow v_{**}$
in other contexts is known to be rather slow [Reference Brunet and Derrida5, Reference Brunet and Derrida6]. Formally showing that this is true for our system as well would be an interesting problem for further research. The results for the uniform jump sizes in Table 2 show the same patterns.
$v_n \uparrow v_{**}$
in other contexts is known to be rather slow [Reference Brunet and Derrida5, Reference Brunet and Derrida6]. Formally showing that this is true for our system as well would be an interesting problem for further research. The results for the uniform jump sizes in Table 2 show the same patterns.
Suppose now that independent jumps and synchronizations by a particle consume some common resource (say, computing power or energy). To be specific, suppose the maximum rate at which the resource may be consumed by a particle is normalized to 1, and the amounts of the resource consumed by one independent jump and one synchronization are
![]() $a>0$
and
$a>0$
and
![]() $b>0$
, respectively. Suppose the aim is to maximize the speed of the particle system. Assume the number of particles is large enough so that
$b>0$
, respectively. Suppose the aim is to maximize the speed of the particle system. Assume the number of particles is large enough so that
![]() $v_n \approx v_{**}$
. Then we obtain the optimization problem
$v_n \approx v_{**}$
. Then we obtain the optimization problem
In the case of exponentially distributed jumps, we have
![]() $v_{**}= (\sqrt{\lambda} + \sqrt{\mu})^2$
, and the problem (11.1) has a simple explicit solution
$v_{**}= (\sqrt{\lambda} + \sqrt{\mu})^2$
, and the problem (11.1) has a simple explicit solution
For a general jump size distribution, the optimal solution
![]() $(\lambda_{opt},\mu_{opt})$
can easily be found numerically using (7.3) and (7.4).
$(\lambda_{opt},\mu_{opt})$
can easily be found numerically using (7.3) and (7.4).
In Tables 1 and 2, for the cases of exponential and uniform jumps, we vary
![]() $(\lambda,\mu)$
while satisfying the constraint
$(\lambda,\mu)$
while satisfying the constraint
![]() $a\lambda+b\mu=1$
with
$a\lambda+b\mu=1$
with
![]() $a=2, b=1$
. In both cases we show
$a=2, b=1$
. In both cases we show
![]() $(\lambda_{opt},\mu_{opt})$
. We see that, even though the values of
$(\lambda_{opt},\mu_{opt})$
. We see that, even though the values of
![]() $v_n$
for
$v_n$
for
![]() $n=10000$
are not necessarily very close to their limiting values
$n=10000$
are not necessarily very close to their limiting values
![]() $v_{**}$
‘yet’ (because this n is not large enough), the parameter setting
$v_{**}$
‘yet’ (because this n is not large enough), the parameter setting
![]() $(\lambda_{opt},\mu_{opt})$
obtained from (11.1) essentially maximizes
$(\lambda_{opt},\mu_{opt})$
obtained from (11.1) essentially maximizes
![]() $v_n$
for this n. Thus, the setting
$v_n$
for this n. Thus, the setting
![]() $(\lambda_{opt},\mu_{opt})$
, which is easily computable, gives a practical rule of thumb for optimizing the trade-off between self-propulsion and synchronization in large-scale systems.
$(\lambda_{opt},\mu_{opt})$
, which is easily computable, gives a practical rule of thumb for optimizing the trade-off between self-propulsion and synchronization in large-scale systems.
12. Proof of Theorem 2
12.1. Characterization of distributional limit
Theorem 10. Suppose
![]() $f^n(0) \stackrel{w}{\rightarrow} f(0)$
, as in Theorem 2. Then the sequence of processes
$f^n(0) \stackrel{w}{\rightarrow} f(0)$
, as in Theorem 2. Then the sequence of processes
![]() $f^n({\cdot})$
is tight in the space
$f^n({\cdot})$
is tight in the space
![]() $D([0,\infty), \mathcal{M}^B)$
, and any sub-sequential distributional limit
$D([0,\infty), \mathcal{M}^B)$
, and any sub-sequential distributional limit
![]() $f({\cdot})$
is such that, with probability one, the trajectory
$f({\cdot})$
is such that, with probability one, the trajectory
![]() $f({\cdot})$
is a continuous element of
$f({\cdot})$
is a continuous element of
![]() $D([0,\infty), \mathcal{M}^B)$
which satisfies (5.3).
$D([0,\infty), \mathcal{M}^B)$
which satisfies (5.3).
Proof. The proof is easily obtained using the steps given in the proof of Theorem 3 in [Reference Stolyar25] (for a different particle system), namely Theorems 4–7 and Corollary 8 in [Reference Stolyar25]. (In turn, the proof of Theorem 3 in [Reference Stolyar25] closely follows the development in [Reference Balázs, Rácz and Tóth1].) The only substantial difference is the verification of the condition (i) of [Reference Perkins24], which in our notation has the following form: for any
![]() $T>0$
and
$T>0$
and
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $K>0$
such that
$K>0$
such that
 \begin{equation}\sup_n \mathbb{P} \left(\sup_{t\le T} [f^n_{-K}(t) + 1- f^n_{K}(t)] >\varepsilon \right) < \varepsilon.\end{equation}
\begin{equation}\sup_n \mathbb{P} \left(\sup_{t\le T} [f^n_{-K}(t) + 1- f^n_{K}(t)] >\varepsilon \right) < \varepsilon.\end{equation}
However, for the process under consideration, with fixed right boundary at the point B, (12.1) is trivial—it suffices to choose K large enough so that
![]() $K > B$
and
$K > B$
and
![]() $f^n_{-K}(0) \le \varepsilon/2$
uniformly in n.
$f^n_{-K}(0) \le \varepsilon/2$
uniformly in n.
12.2. Equivalent characterization of solutions to (5.3) as MFMs
Theorem 11. For any initial condition
![]() $f(0) \in \mathcal{M}^B$
, a trajectory
$f(0) \in \mathcal{M}^B$
, a trajectory
![]() $f({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
satisfies (5.3) if and only if it is an MFM.
$f({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
satisfies (5.3) if and only if it is an MFM.
Proof. This proof is very similar to the proof of Theorem 10 in [Reference Stolyar25].
‘Only if’ statement: We only need to consider points
![]() $x<B$
. Let
$x<B$
. Let
![]() $h=(h(u), \,u\in \mathbb{R})$
be the step function
$h=(h(u), \,u\in \mathbb{R})$
be the step function
![]() $h(u) = {\mathbf{I}}(u \le x)$
, jumping from 1 to 0 at the point x. Let
$h(u) = {\mathbf{I}}(u \le x)$
, jumping from 1 to 0 at the point x. Let
![]() $h_\varepsilon$
,
$h_\varepsilon$
,
![]() $\varepsilon>0$
, be a continuous approximation of h that is linearly decreasing from 1 to 0 in
$\varepsilon>0$
, be a continuous approximation of h that is linearly decreasing from 1 to 0 in
![]() $[x,x+\varepsilon]$
. We see that
$[x,x+\varepsilon]$
. We see that
Indeed,
![]() $|L^B [f(t) h_\varepsilon] - L^B [f(t) h]|$
is upper-bounded by
$|L^B [f(t) h_\varepsilon] - L^B [f(t) h]|$
is upper-bounded by
![]() $(\lambda+1)$
times the probability that a random jump—either independent of the size Z or thanks to synchronization—of a particle randomly located according to the distribution f(t) is such that the jump either originates or lands in
$(\lambda+1)$
times the probability that a random jump—either independent of the size Z or thanks to synchronization—of a particle randomly located according to the distribution f(t) is such that the jump either originates or lands in
![]() $(x,x+\varepsilon)$
; this probability vanishes as
$(x,x+\varepsilon)$
; this probability vanishes as
![]() $\varepsilon\downarrow 0$
. Also, since both
$\varepsilon\downarrow 0$
. Also, since both
![]() $L^B [f(t) h_\varepsilon]$
and
$L^B [f(t) h_\varepsilon]$
and
![]() $L^B [f(t) h_\varepsilon]$
are within
$L^B [f(t) h_\varepsilon]$
are within
![]() $[-(\lambda+1),0]$
, for all t and
$[-(\lambda+1),0]$
, for all t and
![]() $\varepsilon$
, we have a universal bound
$\varepsilon$
, we have a universal bound
![]() $|L [f(t) h_\varepsilon] - L [f(t) h]| \le \lambda+1$
. Then, for any fixed t, by taking the
$|L [f(t) h_\varepsilon] - L [f(t) h]| \le \lambda+1$
. Then, for any fixed t, by taking the
![]() $\varepsilon\downarrow 0$
limit in
$\varepsilon\downarrow 0$
limit in
![]() $f(t) h_\varepsilon - f(0) h_\varepsilon - \int_0^t L^B [f(s) h_\varepsilon] ds =0$
, we obtain
$f(t) h_\varepsilon - f(0) h_\varepsilon - \int_0^t L^B [f(s) h_\varepsilon] ds =0$
, we obtain
This means that
![]() $f(t) h = f_x(t)$
is absolutely continuous in t, with the derivative equal to
$f(t) h = f_x(t)$
is absolutely continuous in t, with the derivative equal to
![]() $(\partial/\partial t) f_x(t)=L^B [f(t) h]$
almost everywhere (with respect to the Lebesgue measure) in t. In particular this implies that for any fixed y, the difference
$(\partial/\partial t) f_x(t)=L^B [f(t) h]$
almost everywhere (with respect to the Lebesgue measure) in t. In particular this implies that for any fixed y, the difference
![]() $f_y(t)-f_{y-}(t)$
is continuous in t (in fact, Lipschitz); this, in turn, means that, possible discontinuity points y of
$f_y(t)-f_{y-}(t)$
is continuous in t (in fact, Lipschitz); this, in turn, means that, possible discontinuity points y of
![]() $f_y(t)$
‘cannot move’ at time t. We can then conclude that, for any x, the derivative
$f_y(t)$
‘cannot move’ at time t. We can then conclude that, for any x, the derivative
![]() $(\partial/\partial t) f_x(t)=L^B [f(t) h]$
is in fact continuous in t. Therefore,
$(\partial/\partial t) f_x(t)=L^B [f(t) h]$
is in fact continuous in t. Therefore,
![]() $(\partial/\partial t) f_x(t)=L^B [f(t) h]$
at every t. It remains to observe that
$(\partial/\partial t) f_x(t)=L^B [f(t) h]$
at every t. It remains to observe that
![]() $L^B [f(t) h]$
is exactly the right-hand side of (5.1).
$L^B [f(t) h]$
is exactly the right-hand side of (5.1).
‘If’ statement: The definition of an MFM
![]() $f({\cdot})$
implies that (5.3) holds for the above-defined step function h for any
$f({\cdot})$
implies that (5.3) holds for the above-defined step function h for any
![]() $x<B$
. Then we have (5.3) for any h, which is piecewise constant with a finite number of pieces; and the set of such functions h is tight within the space of test functions
$x<B$
. Then we have (5.3) for any h, which is piecewise constant with a finite number of pieces; and the set of such functions h is tight within the space of test functions
![]() $h \in \mathcal{C}_b$
, equipped with the uniform metric. Thus (5.3) holds for any
$h \in \mathcal{C}_b$
, equipped with the uniform metric. Thus (5.3) holds for any
![]() $h \in \mathcal{C}_b$
.
$h \in \mathcal{C}_b$
.
12.3. MFM uniqueness
Theorem 12. For any initial condition
![]() $f(0) \in \mathcal{M}^B$
, an MFM
$f(0) \in \mathcal{M}^B$
, an MFM
![]() $f({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
is unique.
$f({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
is unique.
Proof. The existence of an MFM for a given initial state f(0) follows from Theorems 10 and 11. For any MFM
![]() $f({\cdot})$
we know that
$f({\cdot})$
we know that
![]() $f_x(t)$
, as a function of t, is Lipschitz, uniformly in x. Consider two MFM trajectories,
$f_x(t)$
, as a function of t, is Lipschitz, uniformly in x. Consider two MFM trajectories,
![]() $f({\cdot})$
and
$f({\cdot})$
and
![]() $g({\cdot})$
, with the same initial state
$g({\cdot})$
, with the same initial state
![]() $f(0)=g(0)$
. It is easy to check that for any x and any
$f(0)=g(0)$
. It is easy to check that for any x and any
![]() $t>0$
$t>0$
for a fixed constant
![]() $C>0$
(for example, for
$C>0$
(for example, for
![]() $C=2\lambda+1$
). From (12.2) it is easy to see that
$C=2\lambda+1$
). From (12.2) it is easy to see that
as long as
![]() $\| g(t) - f(t) \| >0$
. But then, by Gronwall’s inequality,
$\| g(t) - f(t) \| >0$
. But then, by Gronwall’s inequality,
![]() $\| g(t) - f(t)\| \equiv 0$
. This proves the uniqueness.
$\| g(t) - f(t)\| \equiv 0$
. This proves the uniqueness.
13. Proof of Theorem 1
We now generalize Theorem 2 to Theorem 1. Recall that the evolution of
![]() $f_x^n({\cdot}), x \in ({-}\infty, B),$
is independent of the behavior of particles located in
$f_x^n({\cdot}), x \in ({-}\infty, B),$
is independent of the behavior of particles located in
![]() $[B, \infty)$
. Theorem 2 holds for every B for the projection
$[B, \infty)$
. Theorem 2 holds for every B for the projection
![]() $f^{n,B}({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
of our original process
$f^{n,B}({\cdot}) \in D([0,\infty), \mathcal{M}^B)$
of our original process
![]() $f^{n}({\cdot})$
, and we have convergence to the corresponding unique continuous MFL (MFM)
$f^{n}({\cdot})$
, and we have convergence to the corresponding unique continuous MFL (MFM)
![]() $f^B({\cdot})$
. By uniqueness, these MFLs for different B must be consistent; that is, for any
$f^B({\cdot})$
. By uniqueness, these MFLs for different B must be consistent; that is, for any
![]() $B_1 < B_2$
, any
$B_1 < B_2$
, any
![]() $x< B_1$
, and any t we have
$x< B_1$
, and any t we have
![]() $f_x^{B_1}(t)=f_x^{B_2}(t)$
. So we can formally define a trajectory f(t) by
$f_x^{B_1}(t)=f_x^{B_2}(t)$
. So we can formally define a trajectory f(t) by
![]() $f_x(t) \doteq \lim_{B\uparrow \infty} f_x^B(t)$
. Let us show that this trajectory is the MFL satisfying the statement of Theorem 1.
$f_x(t) \doteq \lim_{B\uparrow \infty} f_x^B(t)$
. Let us show that this trajectory is the MFL satisfying the statement of Theorem 1.
We first show that
![]() $f(t) \in \mathcal{M}$
for any t, i.e.
$f(t) \in \mathcal{M}$
for any t, i.e.
![]() $f_\infty(t) = 1$
. Recall that, for any x,
$f_\infty(t) = 1$
. Recall that, for any x,
![]() $(d/dt)f_x(t)$
is non-positive, bounded, and Lipschitz continuous in t (uniformly in x). Then
$(d/dt)f_x(t)$
is non-positive, bounded, and Lipschitz continuous in t (uniformly in x). Then
![]() $\varepsilon(t) \doteq 1-f_\infty(t)$
is non-decreasing and continuous, starting from 0 at time 0. Moreover,
$\varepsilon(t) \doteq 1-f_\infty(t)$
is non-decreasing and continuous, starting from 0 at time 0. Moreover,
![]() $(d/dt)\varepsilon(t)$
is bounded and Lipschitz continuous. Consider a sequence
$(d/dt)\varepsilon(t)$
is bounded and Lipschitz continuous. Consider a sequence
![]() $c \uparrow \infty$
and the corresponding (non-decreasing) sequence of space-rescaled versions of f(t),
$c \uparrow \infty$
and the corresponding (non-decreasing) sequence of space-rescaled versions of f(t),
Clearly,
![]() $f^{(c)}(t)$
is the limiting trajectory of the process with rescaled initial state and rescaled jumps; and for any t the limit of
$f^{(c)}(t)$
is the limiting trajectory of the process with rescaled initial state and rescaled jumps; and for any t the limit of
![]() $ f_{cx}(t)$
, as a function of x, is constant, equal to
$ f_{cx}(t)$
, as a function of x, is constant, equal to
![]() $1-\varepsilon(t)$
. Consider any fixed
$1-\varepsilon(t)$
. Consider any fixed
![]() $x>0$
and
$x>0$
and
![]() $t>0$
. As
$t>0$
. As
![]() $c\to\infty$
,
$c\to\infty$
,
![]() $1- f^{(c)}_x(t) \to \varepsilon(t)$
and
$1- f^{(c)}_x(t) \to \varepsilon(t)$
and
![]() $(d/dt)f^{(c)}_x(t) \to -\varepsilon(t)(1-\varepsilon(t))$
. For fixed
$(d/dt)f^{(c)}_x(t) \to -\varepsilon(t)(1-\varepsilon(t))$
. For fixed
![]() $t < s$
,
$t < s$
,
We conclude that
![]() $\varepsilon(t)$
, as a function of t, must be a solution to the logistic equation
$\varepsilon(t)$
, as a function of t, must be a solution to the logistic equation
![]() $\varepsilon' = \varepsilon(1-\varepsilon)$
with initial condition
$\varepsilon' = \varepsilon(1-\varepsilon)$
with initial condition
![]() $\varepsilon(0)=0$
. Therefore,
$\varepsilon(0)=0$
. Therefore,
![]() $\varepsilon(t) \equiv 0$
, and then
$\varepsilon(t) \equiv 0$
, and then
![]() $f_\infty(t)\equiv 0$
, i.e.
$f_\infty(t)\equiv 0$
, i.e.
![]() $f(t) \in \mathcal{M}$
.
$f(t) \in \mathcal{M}$
.
Now, because we know that
![]() $f(t) \in \mathcal{M}$
for any t,
$f(t) \in \mathcal{M}$
for any t,
![]() $f({\cdot})$
is clearly an MFM: it satisfies the conditions of Definition 1 for any x (because we can always choose
$f({\cdot})$
is clearly an MFM: it satisfies the conditions of Definition 1 for any x (because we can always choose
![]() $B >x$
). The condition (5.2) holds for any
$B >x$
). The condition (5.2) holds for any
![]() $h \in \mathcal{C}_b$
, because we can choose B large enough so that h(x) is constant in
$h \in \mathcal{C}_b$
, because we can choose B large enough so that h(x) is constant in
![]() $[B,\infty)$
; for such h, the operators
$[B,\infty)$
; for such h, the operators
![]() $L f(t) h = L^B f(t) h$
, and then (5.2) follows from (5.3).
$L f(t) h = L^B f(t) h$
, and then (5.2) follows from (5.3).
It remains to show the convergence
![]() $f^n({\cdot}) \Rightarrow f({\cdot})$
. Fix any
$f^n({\cdot}) \Rightarrow f({\cdot})$
. Fix any
![]() $T>0$
, any
$T>0$
, any
![]() $\varepsilon>0$
, and a sufficiently large
$\varepsilon>0$
, and a sufficiently large
![]() $B=B(T)>0$
so that
$B=B(T)>0$
so that
![]() $1-f_B(T) \le \varepsilon$
. For the modified system with the right boundary at B, we have convergence of
$1-f_B(T) \le \varepsilon$
. For the modified system with the right boundary at B, we have convergence of
![]() $f^{n,B}({\cdot}) \in D([0,T], \mathcal{M}^B)$
to a continuous
$f^{n,B}({\cdot}) \in D([0,T], \mathcal{M}^B)$
to a continuous
![]() $f^{B}({\cdot}) \in D([0,T], \mathcal{M}^B)$
. But since
$f^{B}({\cdot}) \in D([0,T], \mathcal{M}^B)$
. But since
![]() $\varepsilon>0$
can be arbitrarily small, we also have convergence of the original process
$\varepsilon>0$
can be arbitrarily small, we also have convergence of the original process
![]() $f^{n}({\cdot}) \in D([0,T], \mathcal{M})$
to a continuous
$f^{n}({\cdot}) \in D([0,T], \mathcal{M})$
to a continuous
![]() $f({\cdot}) \in D([0,T], \mathcal{M})$
. This is true for arbitrary
$f({\cdot}) \in D([0,T], \mathcal{M})$
. This is true for arbitrary
![]() $T>0$
. Therefore, we also have convergence of the original process
$T>0$
. Therefore, we also have convergence of the original process
![]() $f^{n}({\cdot}) \in D([0,\infty), \mathcal{M})$
to a continuous
$f^{n}({\cdot}) \in D([0,\infty), \mathcal{M})$
to a continuous
![]() $f({\cdot}) \in D([0,\infty), \mathcal{M})$
.
$f({\cdot}) \in D([0,\infty), \mathcal{M})$
.
14. Proof of Theorem 3
The proof is essentially the same as that of Theorems 1 and 2, with straightforward adjustments. The condition (12.1) for this process is automatic.
We only comment on the proof of MFM uniqueness. Note that for any MFM
![]() $f({\cdot})$
, for each x, the derivative
$f({\cdot})$
, for each x, the derivative
![]() $(d/dt) f_x(t)$
can have a discontinuity at time t such that
$(d/dt) f_x(t)$
can have a discontinuity at time t such that
![]() $B=x$
(i.e. when the moving boundary ‘hits’ the point x). However, this does not affect the uniqueness proof in Section 12.3—we just need to note that (12.2) and (12.3) hold for almost any
$B=x$
(i.e. when the moving boundary ‘hits’ the point x). However, this does not affect the uniqueness proof in Section 12.3—we just need to note that (12.2) and (12.3) hold for almost any
![]() $t>0$
with respect to the Lebesgue measure.
$t>0$
with respect to the Lebesgue measure.
15. Proof of Theorem 4
This proof is also essentially the same as that of Theorems 1 and 2, with straightforward adjustments.
Again, we only comment on the proof of MFM uniqueness. An MFM for this system is such that, for a given x, the derivative
![]() $(d/dt) f_x(t)$
may have a discontinuity (a jump down) at any time t such that the jump distribution has an atom at
$(d/dt) f_x(t)$
may have a discontinuity (a jump down) at any time t such that the jump distribution has an atom at
![]() $x-A$
. If we consider two MFM trajectories,
$x-A$
. If we consider two MFM trajectories,
![]() $f({\cdot})$
and
$f({\cdot})$
and
![]() $g({\cdot})$
, with the same initial state
$g({\cdot})$
, with the same initial state
![]() $f(0)=g(0)$
, as in the uniqueness proof in Section 12.3, then for each x, both
$f(0)=g(0)$
, as in the uniqueness proof in Section 12.3, then for each x, both
![]() $(d/dt) f_x(t)$
and
$(d/dt) f_x(t)$
and
![]() $(d/dt) g_x(t)$
will have the same countable set of potential discontinuities in time. We also have that, at any t,
$(d/dt) g_x(t)$
will have the same countable set of potential discontinuities in time. We also have that, at any t,
![]() $f_x(t)$
and
$f_x(t)$
and
![]() $g_x(t)$
, as functions of x, have the same set of discontinuity points. Given these facts, we see that the uniqueness proof in Section 12.3 applies—again, we just need to note that (12.2) and (12.3) hold for almost any
$g_x(t)$
, as functions of x, have the same set of discontinuity points. Given these facts, we see that the uniqueness proof in Section 12.3 applies—again, we just need to note that (12.2) and (12.3) hold for almost any
![]() $t>0$
with respect to the Lebesgue measure.
$t>0$
with respect to the Lebesgue measure.
16. Proof of Theorem 5
For the single-particle independent-jump (Markov) process
![]() $W({\cdot})$
, denote by
$W({\cdot})$
, denote by
![]() $P^t(x,H)$
its transition function and by
$P^t(x,H)$
its transition function and by
![]() $P^t$
its transition operator,
$P^t$
its transition operator,
The generator of this process is
Any function g such that
![]() $1-g \in \mathcal{M}$
(i.e. a complementary distribution function) is within the domain of the generator B, and for such functions, integration by parts in (16.1) gives
$1-g \in \mathcal{M}$
(i.e. a complementary distribution function) is within the domain of the generator B, and for such functions, integration by parts in (16.1) gives
(The integral in (16.2) includes a possible atom of measure
![]() $g_\eta$
at
$g_\eta$
at
![]() $\eta=x$
. If g is continuous, this subtlety is irrelevant.)
$\eta=x$
. If g is continuous, this subtlety is irrelevant.)
Let us fix a function g such that
![]() $1-g \in \mathcal{M}$
, and consider the function
$1-g \in \mathcal{M}$
, and consider the function
Clearly,
![]() $u_x(0)=g_x$
. Note that if
$u_x(0)=g_x$
. Note that if
![]() $g_x = {\mathbf{I}}\{x \le 0\} = \chi_{-x}$
, then
$g_x = {\mathbf{I}}\{x \le 0\} = \chi_{-x}$
, then
![]() $u_x(t) = \mathbb{P}\{\max_i W_i(t) \le 0\}$
. Considering two cases—depending on whether or not the first split of the first particles occurs in [0,t]—we obtain
$u_x(t) = \mathbb{P}\{\max_i W_i(t) \le 0\}$
. Considering two cases—depending on whether or not the first split of the first particles occurs in [0,t]—we obtain
 \begin{align*}u_x(t) = e^{-t} P^t g_x + \int_0^t & e^{-s} P^{s} u^2_x(t-s) ds = e^{-t} P^t g_x + \int_0^t e^{-(t-\xi)} P^{t-\xi} u^2_x(\xi) d\xi,\\[5pt]& e^t u_x(t) = P^t g_x + \int_0^t e^\xi P^{t-\xi} u^2_x(\xi) d\xi.\end{align*}
\begin{align*}u_x(t) = e^{-t} P^t g_x + \int_0^t & e^{-s} P^{s} u^2_x(t-s) ds = e^{-t} P^t g_x + \int_0^t e^{-(t-\xi)} P^{t-\xi} u^2_x(\xi) d\xi,\\[5pt]& e^t u_x(t) = P^t g_x + \int_0^t e^\xi P^{t-\xi} u^2_x(\xi) d\xi.\end{align*}
Differentiating in t, we obtain
then
and finally, recalling (16.2), we have
(It is easy to see from the definition of
![]() $u_x(t)$
that, for any
$u_x(t)$
that, for any
![]() $t>0$
, it is continuous in x. Therefore the subtlety mentioned immediately after (16.2) is irrelevant.)
$t>0$
, it is continuous in x. Therefore the subtlety mentioned immediately after (16.2) is irrelevant.)
Now let
![]() $g_x = {\mathbf{I}}\{x \le 0\}$
. Recall that
$g_x = {\mathbf{I}}\{x \le 0\}$
. Recall that
![]() $u_x(t) = \mathbb{P}\{\max_i W_i(t) \le 0\}$
, and then
$u_x(t) = \mathbb{P}\{\max_i W_i(t) \le 0\}$
, and then
Substituting
![]() $f_x(t)=u_{-x}(t)$
in (16.4), we obtain exactly (5.1) with
$f_x(t)=u_{-x}(t)$
in (16.4), we obtain exactly (5.1) with
![]() $f(0)=\chi$
.
$f(0)=\chi$
.
17. Proof of Theorem 6
The monotonicity,
![]() $v_n \le v_{n+1}$
, has already been observed in (4.1).
$v_n \le v_{n+1}$
, has already been observed in (4.1).
Let us show that
![]() $v_n \le v_{**}$
for all n. The proof of this fact is the same as the proof of the analogous upper bound in Theorem 2.3(4) in [Reference Groisman, Jonckheere and Martínez13], except for our process we need to use Proposition 1, instead of the analogous fact for the process in [Reference Groisman, Jonckheere and Martínez13] (which follows directly from the results of [Reference Kolmogorov, Petrovskii and Piscounov15, Reference McKean23]). Here is the proof, for completeness. Consider the system with a finite number n of particles. Consider another, artificial, system starting with the same initial state with n particles, but such that each initial particle generates its own independent associated BRW as defined above. Clearly, the two systems can be coupled so that the artificial system dominates the actual one in the sense of
$v_n \le v_{**}$
for all n. The proof of this fact is the same as the proof of the analogous upper bound in Theorem 2.3(4) in [Reference Groisman, Jonckheere and Martínez13], except for our process we need to use Proposition 1, instead of the analogous fact for the process in [Reference Groisman, Jonckheere and Martínez13] (which follows directly from the results of [Reference Kolmogorov, Petrovskii and Piscounov15, Reference McKean23]). Here is the proof, for completeness. Consider the system with a finite number n of particles. Consider another, artificial, system starting with the same initial state with n particles, but such that each initial particle generates its own independent associated BRW as defined above. Clearly, the two systems can be coupled so that the artificial system dominates the actual one in the sense of
![]() $\preceq_l$
, and in particular the location of its rightmost particle, M(t), is always to the right of location of the rightmost particle,
$\preceq_l$
, and in particular the location of its rightmost particle, M(t), is always to the right of location of the rightmost particle,
![]() $M_n(t)$
, in the actual system. But Proposition 1 holds for each of the n independent associated BRWs. We infer that
$M_n(t)$
, in the actual system. But Proposition 1 holds for each of the n independent associated BRWs. We infer that
![]() $\limsup_{t\to\infty} M_n(t)/t \le \limsup_{t\to\infty} M(t)/t = v_{**}$
with probability one, which implies
$\limsup_{t\to\infty} M_n(t)/t \le \limsup_{t\to\infty} M(t)/t = v_{**}$
with probability one, which implies
![]() $v_n \le v_{**}$
.
$v_n \le v_{**}$
.
It remains to show that
![]() $\liminf_n v_n \ge v_{**}.$
Consider an arbitrary initial state of the process with n particles. Suppose without loss of generality that the leading particle is initially at 0, and let
$\liminf_n v_n \ge v_{**}.$
Consider an arbitrary initial state of the process with n particles. Suppose without loss of generality that the leading particle is initially at 0, and let
![]() $D_n(t)$
be the location of the leading particle at time t. Consider a modified process such that all particles except the leading one are initially placed at
$D_n(t)$
be the location of the leading particle at time t. Consider a modified process such that all particles except the leading one are initially placed at
![]() $-\infty$
. By monotonicity, the location
$-\infty$
. By monotonicity, the location
![]() $\tilde D_n(t)$
of the leading particle in the modified system is stochastically dominated by
$\tilde D_n(t)$
of the leading particle in the modified system is stochastically dominated by
![]() $D_n(t)$
. The modified process is such that, in particular, at some points in time some particles located at
$D_n(t)$
. The modified process is such that, in particular, at some points in time some particles located at
![]() $-\infty$
will jump forward to join particles in
$-\infty$
will jump forward to join particles in
![]() $[0,\infty)$
; let us call the particles located in
$[0,\infty)$
; let us call the particles located in
![]() $[0,\infty)$
regular. Let us now fix a finite time interval [0,T], and consider the limit of the process of regular particles in this time interval as
$[0,\infty)$
regular. Let us now fix a finite time interval [0,T], and consider the limit of the process of regular particles in this time interval as
![]() $n\to\infty$
. It is easy to construct a coupling such that, with probability one, the process of regular particles (of the modified system) converges to an associated BRW. (Indeed, when n is large, the rate at which each regular particle is being joined by a particle from
$n\to\infty$
. It is easy to construct a coupling such that, with probability one, the process of regular particles (of the modified system) converges to an associated BRW. (Indeed, when n is large, the rate at which each regular particle is being joined by a particle from
![]() $-\infty$
is close to 1. We omit the details, which are straightforward.) By Proposition 1, if T is sufficiently large, then the average speed of advance of the leading particle of the BRW in [0,T] is close to
$-\infty$
is close to 1. We omit the details, which are straightforward.) By Proposition 1, if T is sufficiently large, then the average speed of advance of the leading particle of the BRW in [0,T] is close to
![]() $v_{**}$
. (This is if
$v_{**}$
. (This is if
![]() $\alpha>0$
and then
$\alpha>0$
and then
![]() $v_{**} < \infty$
. If
$v_{**} < \infty$
. If
![]() $\alpha=0$
and then
$\alpha=0$
and then
![]() $v_{**} = \infty$
, ‘close to
$v_{**} = \infty$
, ‘close to
![]() $v_{**}$
’ means ‘arbitrarily large’.) Consequently, for all large n, the average speed of advance of
$v_{**}$
’ means ‘arbitrarily large’.) Consequently, for all large n, the average speed of advance of
![]() $\tilde D_n(t)$
is close to
$\tilde D_n(t)$
is close to
![]() $v_{**}$
. This implies (we skip straightforward
$v_{**}$
. This implies (we skip straightforward
![]() $\varepsilon$
–
$\varepsilon$
–
![]() $\delta$
formalities) that
$\delta$
formalities) that
![]() $\liminf_n v_n \ge v_{**}$
.
$\liminf_n v_n \ge v_{**}$
.
18. Existence and properties of traveling waves in the case of exponentially distributed jump sizes; proof of Theorem 7
In this section we consider the case of exponential jump size distribution,
![]() $J(x) =1- e^{-x}$
, and develop results leading to the proof of Theorem 7.
$J(x) =1- e^{-x}$
, and develop results leading to the proof of Theorem 7.
Recall that in this case a TWS
![]() $\phi=(\phi_x)$
must satisfy the ODE (6.4):
$\phi=(\phi_x)$
must satisfy the ODE (6.4):
A function
![]() $\phi=(\phi_x)$
is a TWS for our original system if and only if it is a proper solution of the ODE (18.1)—that is, if and only if
$\phi=(\phi_x)$
is a TWS for our original system if and only if it is a proper solution of the ODE (18.1)—that is, if and only if
![]() $\phi_x \in [0,1]$
for all
$\phi_x \in [0,1]$
for all
![]() $x \in \mathbb{R}$
, (18.1) holds for all
$x \in \mathbb{R}$
, (18.1) holds for all
![]() $x \in \mathbb{R}$
,
$x \in \mathbb{R}$
,
![]() $\lim_{x \downarrow -\infty} \phi_x = 0$
, and
$\lim_{x \downarrow -\infty} \phi_x = 0$
, and
![]() $\lim_{x \uparrow \infty} \phi_x = 1$
.
$\lim_{x \uparrow \infty} \phi_x = 1$
.
It will be convenient to consider the ODE (18.1) in terms of the first-order ODE in phase space
![]() $(\phi, z=\phi')$
:
$(\phi, z=\phi')$
:
In terms of (18.2), a proper solution is a solution which starts at the point (0,0), ends at the point (1, 0), and stays within the strip
![]() $\phi \in [0,1]$
.
$\phi \in [0,1]$
.
The following are immediate observations from (18.2). Solutions to (18.2) (not necessarily proper solutions) have the following properties: a solution trajectory cannot hit the
![]() $\phi$
-axis for
$\phi$
-axis for
![]() $\phi\in (0,1)$
; given any two solution trajectories, either they coincide for
$\phi\in (0,1)$
; given any two solution trajectories, either they coincide for
![]() $\phi \in [0,1]$
or one strictly dominates another for
$\phi \in [0,1]$
or one strictly dominates another for
![]() $\phi \in (0,1)$
.
$\phi \in (0,1)$
.
18.1. Lower bound on speed v, for any proper solution
Consider the linearization of (18.2) at the point (1, 0). If we set
![]() $\nu=1-\phi$
, the linearization is
$\nu=1-\phi$
, the linearization is
The eigenvalues of this linear system satisfy the characteristic equation
We know (see Section 6) that for a proper solution to exist, we must have
![]() $v\ge \lambda$
. Given that,
$v\ge \lambda$
. Given that,
![]() $-(1+v-\lambda) < 0$
, and it is easy to check that the condition
$-(1+v-\lambda) < 0$
, and it is easy to check that the condition
![]() $(1+v-\lambda)^2 -4v \ge 0$
is equivalent to the condition
$(1+v-\lambda)^2 -4v \ge 0$
is equivalent to the condition
![]() $v \ge v_* \doteq (1+\sqrt{\lambda})^2$
. We see that both eigenvalues of (18.3) (roots of (18.4)) have negative real parts; the eigenvalues are two (different) adjoint complex numbers if and only if
$v \ge v_* \doteq (1+\sqrt{\lambda})^2$
. We see that both eigenvalues of (18.3) (roots of (18.4)) have negative real parts; the eigenvalues are two (different) adjoint complex numbers if and only if
![]() $v<(1+\sqrt{\lambda})^2$
, and they are both real otherwise. We then observe that when
$v<(1+\sqrt{\lambda})^2$
, and they are both real otherwise. We then observe that when
![]() $v<(1+\sqrt{\lambda})^2$
, a proper solution does not exist, because any solution with endpoint at (1, 0) converges to (1, 0) by oscillating around it (as illustrated in Figure 1) and thus must ‘hit’ the line
$v<(1+\sqrt{\lambda})^2$
, a proper solution does not exist, because any solution with endpoint at (1, 0) converges to (1, 0) by oscillating around it (as illustrated in Figure 1) and thus must ‘hit’ the line
![]() $\phi=1$
at a point strictly above the point (1, 0).
$\phi=1$
at a point strictly above the point (1, 0).

Figure 1. Vector field
![]() $(\phi',z')$
in the vicinity of (1, 0);
$(\phi',z')$
in the vicinity of (1, 0);
![]() $\lambda=4$
,
$\lambda=4$
,
![]() $v=7 < v_*=9$
.
$v=7 < v_*=9$
.
We conclude that if a proper solution of (18.2) exists, then necessarily
![]() $v\ge v_* = (1+\sqrt{\lambda})^2.$
$v\ge v_* = (1+\sqrt{\lambda})^2.$
18.2. Proof of Theorem 7(i)
To complete the proof of Theorem 9(i), we need to show that a a proper solution of (18.2) exists for any
![]() $v \ge v_*$
. We will prove that it exists for
$v \ge v_*$
. We will prove that it exists for
![]() $v> v_*$
, and then will obtain the existence for
$v> v_*$
, and then will obtain the existence for
![]() $v=v_*$
by continuity.
$v=v_*$
by continuity.
18.2.1. Existence, uniqueness, and continuity of solutions to (18.2)
Here we consider solutions to (18.2) (not necessarily proper solutions) within the domain
![]() $\{0\le \phi \le 1, \,z\ge 0\}$
. Consider a fixed parameter
$\{0\le \phi \le 1, \,z\ge 0\}$
. Consider a fixed parameter
![]() $v \ge v_*$
and an initial condition
$v \ge v_*$
and an initial condition
![]() $(\phi_0,z_0)$
for a solution to (18.2). (The initial condition can be viewed as a point which a solution trajectory must contain, because the trajectories satisfying (18.2) can be considered in both the forward and the reverse direction.) From the standard theory of ODEs, we see that the solution for a given triple
$(\phi_0,z_0)$
for a solution to (18.2). (The initial condition can be viewed as a point which a solution trajectory must contain, because the trajectories satisfying (18.2) can be considered in both the forward and the reverse direction.) From the standard theory of ODEs, we see that the solution for a given triple
![]() $(\phi_0,z_0,v)$
exists and is unique as long as
$(\phi_0,z_0,v)$
exists and is unique as long as
![]() $(\phi_0,z_0)\ne (0,0)$
and
$(\phi_0,z_0)\ne (0,0)$
and
![]() $(\phi_0,z_0)\ne (1, 0)$
. Moreover, the solution is continuous in
$(\phi_0,z_0)\ne (1, 0)$
. Moreover, the solution is continuous in
![]() $(\phi_0,z_0,v)$
outside those two points. The following lemma shows that the existence, uniqueness, and continuity hold for the initial condition
$(\phi_0,z_0,v)$
outside those two points. The following lemma shows that the existence, uniqueness, and continuity hold for the initial condition
![]() $(\phi_0,z_0)= (0,0)$
as well, if we consider non-trivial solutions.
$(\phi_0,z_0)= (0,0)$
as well, if we consider non-trivial solutions.
Lemma 2. For a fixed
![]() $\lambda >0$
and any speed
$\lambda >0$
and any speed
![]() $v\ge v_*$
, there exists a unique non-trivial solution
$v\ge v_*$
, there exists a unique non-trivial solution
![]() $(\phi, z(\phi))$
such that
$(\phi, z(\phi))$
such that
![]() $z(\phi)>0$
and
$z(\phi)>0$
and
![]() $(\phi, z(\phi)) \to (0,0)$
as
$(\phi, z(\phi)) \to (0,0)$
as
![]() $\phi\downarrow 0$
. This solution is such that
$\phi\downarrow 0$
. This solution is such that
![]() $dz/d\phi = \gamma$
at the initial
$dz/d\phi = \gamma$
at the initial
![]() $\phi=0$
, where
$\phi=0$
, where
Moreover, the solution is continuous with respect to
![]() $(\phi_0,z_0,v)$
.
$(\phi_0,z_0,v)$
.
Proof of Lemma 2. Recall that
![]() $v \ge v_* > 1+ \lambda$
. Then, for the linearization of (18.2) at the point (0,0), we always have two different real eigenvalues, one positive and one negative:
$v \ge v_* > 1+ \lambda$
. Then, for the linearization of (18.2) at the point (0,0), we always have two different real eigenvalues, one positive and one negative:
![]() $-\gamma_2 < 0 < \gamma$
, where
$-\gamma_2 < 0 < \gamma$
, where
![]() $\gamma$
is given by (18.5). The corresponding eigenvectors are
$\gamma$
is given by (18.5). The corresponding eigenvectors are
![]() $(1,\gamma)$
and
$(1,\gamma)$
and
![]() $(1,-\gamma_2)$
; see Figure 2.
$(1,-\gamma_2)$
; see Figure 2.

Figure 2. Vector field
![]() $(\phi',z')$
in the vicinity of (0,0);
$(\phi',z')$
in the vicinity of (0,0);
![]() $\lambda=4$
,
$\lambda=4$
,
![]() $v=10$
,
$v=10$
,
![]() $v > v_*$
.
$v > v_*$
.
The proof of existence is constructive. Consider any sequence of solutions, each starting at a point
![]() $(\phi^{(k)}_0, z^{(k)}_0) \ge (0,0)$
and corresponding to a speed
$(\phi^{(k)}_0, z^{(k)}_0) \ge (0,0)$
and corresponding to a speed
![]() $v^{(k)} \ge v_*$
; the sequence is such that, as
$v^{(k)} \ge v_*$
; the sequence is such that, as
![]() $n\to\infty$
,
$n\to\infty$
,
![]() $(\phi^{(k)}_0, z^{(k)}_0) \to (0,0)$
,
$(\phi^{(k)}_0, z^{(k)}_0) \to (0,0)$
,
![]() $v^{(k)} \to v$
, and
$v^{(k)} \to v$
, and
![]() $(\phi^{(k)}_0, z^{(k)}_0) \ne (0,0)$
for all k. We view these solutions as functions
$(\phi^{(k)}_0, z^{(k)}_0) \ne (0,0)$
for all k. We view these solutions as functions
![]() $z^{(k)}=z^{(k)}(\phi)$
; this is possible because
$z^{(k)}=z^{(k)}(\phi)$
; this is possible because
![]() $\phi'=z>0$
for
$\phi'=z>0$
for
![]() $\phi \in (\phi_0, 1)$
. Then any sub-sequential limit of this sequence of solutions must be a solution
$\phi \in (\phi_0, 1)$
. Then any sub-sequential limit of this sequence of solutions must be a solution
![]() $z=z(\phi)$
(with speed parameter v) starting from (0,0). Also, given the structure of the derivative vector field around (0,0), it is easy to see that any such solution must satisfy
$z=z(\phi)$
(with speed parameter v) starting from (0,0). Also, given the structure of the derivative vector field around (0,0), it is easy to see that any such solution must satisfy
![]() $dz/d\phi = \gamma$
at
$dz/d\phi = \gamma$
at
![]() $\phi=0$
. (Indeed, for
$\phi=0$
. (Indeed, for
![]() $c>0$
, denote by
$c>0$
, denote by
![]() $M_c = \{z=c\phi, \,\phi \ge 0\}$
the ray from the point (0,0) in the direction (1,c). For a small fixed
$M_c = \{z=c\phi, \,\phi \ge 0\}$
the ray from the point (0,0) in the direction (1,c). For a small fixed
![]() $\varepsilon>0$
, denote by W the closed cone between the rays
$\varepsilon>0$
, denote by W the closed cone between the rays
![]() $M_{\gamma-\varepsilon}$
and
$M_{\gamma-\varepsilon}$
and
![]() $M_{\gamma+\varepsilon}$
. If we look at the solution in the reverse direction, as it approaches the point (0,0), it cannot be outside W arbitrarily close to (0,0)—otherwise it will hit the z-axis strictly above (0,0).)
$M_{\gamma+\varepsilon}$
. If we look at the solution in the reverse direction, as it approaches the point (0,0), it cannot be outside W arbitrarily close to (0,0)—otherwise it will hit the z-axis strictly above (0,0).)
It remains to show the uniqueness of a solution for a given parameter v. (Then the continuity in
![]() $(\phi_0,z_0,v)$
will automatically follow.) Consider any two solutions to (18.2), viewed as functions
$(\phi_0,z_0,v)$
will automatically follow.) Consider any two solutions to (18.2), viewed as functions
![]() $z=z(\phi)$
and
$z=z(\phi)$
and
![]() $\hat z= \hat z(\phi)$
. It is easy to see from (18.2) that
$\hat z= \hat z(\phi)$
. It is easy to see from (18.2) that
Thus, the difference
![]() $\hat z(\phi) - z(\phi)$
cannot increase in
$\hat z(\phi) - z(\phi)$
cannot increase in
![]() $\phi$
, which implies uniqueness.
$\phi$
, which implies uniqueness.
18.2.2. Existence of a proper solution for
 $v \ge v_*$
$v \ge v_*$
Lemma 3. A proper solution of (18.2) exists for any
![]() $v>v_*$
. (Furthermore, by continuity of solutions in v, it exists for
$v>v_*$
. (Furthermore, by continuity of solutions in v, it exists for
![]() $v=v_*$
as well.)
$v=v_*$
as well.)
Proof of Lemma 3. Consider
![]() $C>1$
(to be determined later). Consider a point
$C>1$
(to be determined later). Consider a point
![]() $(\phi,z)$
, with
$(\phi,z)$
, with
![]() $\phi\in (0,1)$
and
$\phi\in (0,1)$
and
![]() $z\ge 0$
. Let us compare the derivative vector
$z\ge 0$
. Let us compare the derivative vector
![]() $(\phi',z')$
, given by (18.2), to the tangent vector to the parabola
$(\phi',z')$
, given by (18.2), to the tangent vector to the parabola
![]() $h(\phi) = C \phi(1-\phi)/v$
at the point
$h(\phi) = C \phi(1-\phi)/v$
at the point
![]() $\phi$
, with the
$\phi$
, with the
![]() $\phi$
-component equal to
$\phi$
-component equal to
![]() $\phi'$
; the tangent vector is then
$\phi'$
; the tangent vector is then
![]() $(\phi', \phi' C(1-2\phi)/v)$
. The difference between the z-components of these two vectors is
$(\phi', \phi' C(1-2\phi)/v)$
. The difference between the z-components of these two vectors is
If
![]() $(\phi,z)=(\phi, h(\phi))$
, i.e. the point
$(\phi,z)=(\phi, h(\phi))$
, i.e. the point
![]() $(\phi,z)$
is on the parabola, this difference is
$(\phi,z)$
is on the parabola, this difference is
Let us consider the expression in the bracket (a linear function of
![]() $\phi$
). If we can prove that it is positive for
$\phi$
). If we can prove that it is positive for
![]() $0\leq \phi\leq 1$
, then the trajectories of our dynamic system will traverse the parabola
$0\leq \phi\leq 1$
, then the trajectories of our dynamic system will traverse the parabola
![]() $h=C\phi(1-\phi)/v$
entering the domain between that parabola and
$h=C\phi(1-\phi)/v$
entering the domain between that parabola and
![]() $\phi$
-axis. (See Figure 3.) Let us check that this is the case. The coefficient in front of
$\phi$
-axis. (See Figure 3.) Let us check that this is the case. The coefficient in front of
![]() $\phi$
is negative, so it suffices to check the expression is positive at
$\phi$
is negative, so it suffices to check the expression is positive at
![]() $\phi=1$
, i.e.
$\phi=1$
, i.e.
The condition
![]() $v>(1+\sqrt{\lambda})^2$
is equivalent to
$v>(1+\sqrt{\lambda})^2$
is equivalent to
![]() $\sqrt{v}>1+\sqrt{\lambda}$
, then to
$\sqrt{v}>1+\sqrt{\lambda}$
, then to
![]() $(\sqrt{v}-1)^2>\lambda$
, then to
$(\sqrt{v}-1)^2>\lambda$
, then to
![]() $v-\lambda+1>2\sqrt{v}$
. If we take
$v-\lambda+1>2\sqrt{v}$
. If we take
![]() $C=\sqrt{v}$
, this gives exactly the last display.
$C=\sqrt{v}$
, this gives exactly the last display.

Figure 3. Vector field
![]() $(\phi',z')$
, for points inside the domain between the parabolas
$(\phi',z')$
, for points inside the domain between the parabolas
![]() $z = C \phi(1-\phi)/v$
and
$z = C \phi(1-\phi)/v$
and
![]() $z=\phi(1-\phi)/v$
; here
$z=\phi(1-\phi)/v$
; here
![]() $C=\sqrt{v}$
,
$C=\sqrt{v}$
,
![]() $\lambda=4$
,
$\lambda=4$
,
![]() $v=10$
,
$v=10$
,
![]() $v > v_*$
.
$v > v_*$
.
Now, consider the solution
![]() $z(\phi)$
to (18.2) with initial condition (0,0). The derivative
$z(\phi)$
to (18.2) with initial condition (0,0). The derivative
![]() $dz/d\phi$
at
$dz/d\phi$
at
![]() $\phi=0$
is
$\phi=0$
is
![]() $\gamma$
(in (18.5)), while the derivative of
$\gamma$
(in (18.5)), while the derivative of
![]() $h(\phi)$
(with
$h(\phi)$
(with
![]() $C=\sqrt{v}$
) is
$C=\sqrt{v}$
) is
![]() $1/\sqrt{v}$
. For
$1/\sqrt{v}$
. For
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $v \ge v_*$
, the inequality
$v \ge v_*$
, the inequality
![]() $1/\sqrt{v} > \gamma$
can be verified by simple algebra. This means that, for sufficiently small
$1/\sqrt{v} > \gamma$
can be verified by simple algebra. This means that, for sufficiently small
![]() $\phi>0$
, the solution
$\phi>0$
, the solution
![]() $z(\phi)$
is ‘under’ the parabola
$z(\phi)$
is ‘under’ the parabola
![]() $h(\phi)$
. But, as shown above, it cannot traverse
$h(\phi)$
. But, as shown above, it cannot traverse
![]() $h(\phi)$
. We also know that the solution
$h(\phi)$
. We also know that the solution
![]() $z(\phi)$
cannot hit the
$z(\phi)$
cannot hit the
![]() $\phi$
-axis while
$\phi$
-axis while
![]() $\phi\in (0,1)$
. We conclude that
$\phi\in (0,1)$
. We conclude that
![]() $z(\phi) \le h(\phi)$
for all
$z(\phi) \le h(\phi)$
for all
![]() $\phi \le 1$
, and
$\phi \le 1$
, and
![]() $z(1)=0$
. In particular,
$z(1)=0$
. In particular,
![]() $z(\phi)$
is a proper solution. (In fact, one can show that the trajectories also are transversal to the parabola
$z(\phi)$
is a proper solution. (In fact, one can show that the trajectories also are transversal to the parabola
![]() $z=\phi(1-\phi)/v$
.)
$z=\phi(1-\phi)/v$
.)
18.2.3. Derivative of the proper solution at the point (1, 0)
To complete the proof of of Theorem 7(i), it remains to show that (9.1) holds when
![]() $v > v_*$
. If
$v > v_*$
. If
![]() $v>v_*$
, the linearization of our dynamic system at the point (1, 0) has two strictly negative eigenvalues,
$v>v_*$
, the linearization of our dynamic system at the point (1, 0) has two strictly negative eigenvalues,
![]() $-\zeta_1 > -\zeta_2,$
, being roots of (18.4), so that
$-\zeta_1 > -\zeta_2,$
, being roots of (18.4), so that
Since the solution
![]() $z=z(\phi)$
for speed v is dominated by the parabola
$z=z(\phi)$
for speed v is dominated by the parabola
![]() $\phi(1-\phi)/\sqrt{v}$
, we see that in the neighborhood of (1, 0) it is dominated by the line
$\phi(1-\phi)/\sqrt{v}$
, we see that in the neighborhood of (1, 0) it is dominated by the line
![]() $z=(1-\phi)/\sqrt{v}$
. It is easy to see that
$z=(1-\phi)/\sqrt{v}$
. It is easy to see that
![]() $1/\sqrt{v} < \zeta_2$
. (Indeed, the stronger inequality
$1/\sqrt{v} < \zeta_2$
. (Indeed, the stronger inequality
![]() $1/\sqrt{v} < (1+v-\lambda)/(2v)$
is equivalent to
$1/\sqrt{v} < (1+v-\lambda)/(2v)$
is equivalent to
![]() $v > v_*$
.) Therefore, in the neighborhood of (1, 0) the solution
$v > v_*$
.) Therefore, in the neighborhood of (1, 0) the solution
![]() $z=z(\phi)$
is separated from the eigendirection
$z=z(\phi)$
is separated from the eigendirection
![]() $z=\zeta_2 (1-\phi)$
by line
$z=\zeta_2 (1-\phi)$
by line
![]() $z=(1-\phi)/\sqrt{v}$
. But then the solution
$z=(1-\phi)/\sqrt{v}$
. But then the solution
![]() $z=z(\phi)$
must approach the point (1, 0) along the eigendirection
$z=z(\phi)$
must approach the point (1, 0) along the eigendirection
![]() $z=\zeta_1 (1-\phi)$
, that is
$z=\zeta_1 (1-\phi)$
, that is
It remains to notice that
![]() $\zeta_1$
is exactly equal to
$\zeta_1$
is exactly equal to
![]() $\zeta(v)$
in (7.8).
$\zeta(v)$
in (7.8).
18.3. Existence of solutions giving TWS for systems with moving left or right boundary; proof of Theorem 7(ii)–(iii)
The following theorem is an extended version of Theorem 7(ii).
Theorem 13. Suppose
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $v>v_*$
. For any sufficiently small
$v>v_*$
. For any sufficiently small
![]() $\phi_0>0$
and
$\phi_0>0$
and
![]() $z_0=\phi_0(1-\phi_0 + \lambda)/v$
, the solution to (18.2) with initial condition
$z_0=\phi_0(1-\phi_0 + \lambda)/v$
, the solution to (18.2) with initial condition
![]() $(\phi_0,z_0)$
ends at (1, 0). This solution corresponds to the unique (up to a shift) TWS
$(\phi_0,z_0)$
ends at (1, 0). This solution corresponds to the unique (up to a shift) TWS
![]() $\phi=(\phi_x)$
for the system with moving left boundary at speed v, satisfying the conditions
$\phi=(\phi_x)$
for the system with moving left boundary at speed v, satisfying the conditions
![]() $\phi_{x_0}=\phi_0$
,
$\phi_{x_0}=\phi_0$
,
![]() $\phi^{\prime}_{x_0}=z_0$
, where
$\phi^{\prime}_{x_0}=z_0$
, where
![]() $x_0$
is the left boundary point of the TWS; moreover, the TWS
$x_0$
is the left boundary point of the TWS; moreover, the TWS
![]() $\phi$
satisfies (9.1).
$\phi$
satisfies (9.1).
Proof of Theorem 13. Since
![]() $v>v_*$
, there is a unique solution
$v>v_*$
, there is a unique solution
![]() $z(\phi)$
to (18.2) with initial condition (0,0), and it is proper. Moreover, this solution is ‘under’ the parabola
$z(\phi)$
to (18.2) with initial condition (0,0), and it is proper. Moreover, this solution is ‘under’ the parabola
![]() $h(\phi)=\sqrt{v} \phi(1-\phi)/v$
, as shown in the proof of Lemma 3. Let us consider the solution
$h(\phi)=\sqrt{v} \phi(1-\phi)/v$
, as shown in the proof of Lemma 3. Let us consider the solution
![]() $\hat z(\phi)$
to (18.2) with initial condition
$\hat z(\phi)$
to (18.2) with initial condition
![]() $(0,\varepsilon)$
, for small
$(0,\varepsilon)$
, for small
![]() $\varepsilon>0$
. By continuity of solutions to (18.2) in initial condition, we can choose
$\varepsilon>0$
. By continuity of solutions to (18.2) in initial condition, we can choose
![]() $\varepsilon$
small enough so that
$\varepsilon$
small enough so that
![]() $\hat z(\phi)$
is close to
$\hat z(\phi)$
is close to
![]() $z(\phi)$
and therefore is under the
$z(\phi)$
and therefore is under the
![]() $h(\phi)$
for some values
$h(\phi)$
for some values
![]() $\phi \in (0,1)$
. We conclude (as in the proof of Lemma 3) that solution
$\phi \in (0,1)$
. We conclude (as in the proof of Lemma 3) that solution
![]() $\hat z(\phi)$
for
$\hat z(\phi)$
for
![]() $\phi \in [0,1]$
ends at the point (1, 0). We also know that
$\phi \in [0,1]$
ends at the point (1, 0). We also know that
![]() $z(\phi) < \hat z(\phi)$
for all
$z(\phi) < \hat z(\phi)$
for all
![]() $\phi \in [0,1)$
. Recall that the derivative
$\phi \in [0,1)$
. Recall that the derivative
![]() $dz/d\phi$
at
$dz/d\phi$
at
![]() $\phi=0$
is equal to
$\phi=0$
is equal to
![]() $\gamma$
in (18.5). The dependence
$\gamma$
in (18.5). The dependence
![]() $z_0=\phi_0(1-\phi_0 + \lambda)/v$
on
$z_0=\phi_0(1-\phi_0 + \lambda)/v$
on
![]() $\phi_0$
has derivative
$\phi_0$
has derivative
![]() $(1+\lambda)/v$
at
$(1+\lambda)/v$
at
![]() $\phi_0=0$
. The inequality
$\phi_0=0$
. The inequality
![]() $(1+\lambda)/v > \gamma$
is verified by simple algebra. We conclude the following: for all sufficiently small positive
$(1+\lambda)/v > \gamma$
is verified by simple algebra. We conclude the following: for all sufficiently small positive
![]() $\phi_0$
, the point
$\phi_0$
, the point
![]() $(z_0,\phi_0)$
lies strictly between the solutions
$(z_0,\phi_0)$
lies strictly between the solutions
![]() $z(\phi)$
and
$z(\phi)$
and
![]() $\hat z(\phi)$
. Therefore, the unique solution to (18.2) with initial condition
$\hat z(\phi)$
. Therefore, the unique solution to (18.2) with initial condition
![]() $(z_0,\phi_0)$
ends at the point (1, 0).
$(z_0,\phi_0)$
ends at the point (1, 0).
Verification of (9.1) for the corresponding TWS
![]() $\phi$
is the same as in the proof of Theorem 7(i).
$\phi$
is the same as in the proof of Theorem 7(i).
Proof of Theorem 7(iii). There is a unique solution to (18.2) with initial condition (0,0). Since
![]() $v<v_*$
, this solution cannot be proper. Therefore, the solution ‘hits’ the line
$v<v_*$
, this solution cannot be proper. Therefore, the solution ‘hits’ the line
![]() $\phi=1$
strictly above the
$\phi=1$
strictly above the
![]() $\phi$
-axis, i.e. at a point
$\phi$
-axis, i.e. at a point
![]() $(1,z_1)$
with
$(1,z_1)$
with
![]() $z_1>0$
. The corresponding (unique up to a shift) distribution function
$z_1>0$
. The corresponding (unique up to a shift) distribution function
![]() $\phi=(\phi_x)$
is the unique TWS for the system with moving right boundary at speed v.
$\phi=(\phi_x)$
is the unique TWS for the system with moving right boundary at speed v.
19. Proof of Theorem 8
Consider a fixed MFL
![]() $f({\cdot})$
. Let us fix an arbitrarily small
$f({\cdot})$
. Let us fix an arbitrarily small
![]() $\nu>0$
. Without loss of generality, assume that
$\nu>0$
. Without loss of generality, assume that
![]() $f_0(0) \ge \nu$
and
$f_0(0) \ge \nu$
and
![]() $f_{0-}(0) \le \nu$
. Recall that the trajectory
$f_{0-}(0) \le \nu$
. Recall that the trajectory
![]() $f({\cdot})$
is the unique distributional limit of a sequence of processes
$f({\cdot})$
is the unique distributional limit of a sequence of processes
![]() $f^n({\cdot})$
with deterministic initial states such that
$f^n({\cdot})$
with deterministic initial states such that
![]() $f^n(0) \stackrel{w}{\rightarrow} f(0)$
. We can and will choose a sequence of initial states such that, for all n,
$f^n(0) \stackrel{w}{\rightarrow} f(0)$
. We can and will choose a sequence of initial states such that, for all n,
![]() $\nu n$
of the leftmost particles are located in
$\nu n$
of the leftmost particles are located in
![]() $({-}\infty,0]$
(let us call them ‘left particles’) and then the remaining
$({-}\infty,0]$
(let us call them ‘left particles’) and then the remaining
![]() $(1-\nu)n$
particles are located in
$(1-\nu)n$
particles are located in
![]() $[0,\infty)$
(let us call them ‘right particles’).
$[0,\infty)$
(let us call them ‘right particles’).
Now, for each n, consider a lower-bounding process
![]() $\hat f^n({\cdot})$
constructed as follows. The initial state of
$\hat f^n({\cdot})$
constructed as follows. The initial state of
![]() $\hat f^n({\cdot})$
is such that the
$\hat f^n({\cdot})$
is such that the
![]() $\nu n$
‘left’ particles’ locations are the same as in the original process, i.e.
$\nu n$
‘left’ particles’ locations are the same as in the original process, i.e.
![]() $\hat f_x^n(0) = f_x^n(0)$
for
$\hat f_x^n(0) = f_x^n(0)$
for
![]() $x< 0$
, while the
$x< 0$
, while the
![]() $(1-\nu) n$
‘right’ particles are located exactly at 0. The evolution of
$(1-\nu) n$
‘right’ particles are located exactly at 0. The evolution of
![]() $\hat f^n({\cdot})$
is such that the ‘left’ particles are ‘frozen’—they do not jump at all; the ‘right’ particles jump as usual, making both independent and synchronization jumps. Clearly,
$\hat f^n({\cdot})$
is such that the ‘left’ particles are ‘frozen’—they do not jump at all; the ‘right’ particles jump as usual, making both independent and synchronization jumps. Clearly,
![]() $\hat f^n({\cdot})$
and
$\hat f^n({\cdot})$
and
![]() $f^n({\cdot})$
can be coupled so that
$f^n({\cdot})$
can be coupled so that
![]() $\hat f^n(t) \preceq f^n(t)$
at all times; then
$\hat f^n(t) \preceq f^n(t)$
at all times; then
![]() $\hat f(t) \preceq f(t)$
for the corresponding MFLs. Now, observe that the evolution of
$\hat f(t) \preceq f(t)$
for the corresponding MFLs. Now, observe that the evolution of
![]() $\hat f^n({\cdot})$
is such that the left particles can simply be ignored, and all of the right particles are initially at 0. Next observe that the process
$\hat f^n({\cdot})$
is such that the left particles can simply be ignored, and all of the right particles are initially at 0. Next observe that the process
![]() $\hat f^n({\cdot})$
is such that the evolution of the set of
$\hat f^n({\cdot})$
is such that the evolution of the set of
![]() $(1-\nu)n$
right particles can be viewed as that of a stand-alone original system, except the synchronization rate of each particle is
$(1-\nu)n$
right particles can be viewed as that of a stand-alone original system, except the synchronization rate of each particle is
![]() $(1-\nu)$
instead of 1. (Recall that in the system under consideration we have
$(1-\nu)$
instead of 1. (Recall that in the system under consideration we have
![]() $\mu=1$
, without loss of generality.) Therefore, the MFL
$\mu=1$
, without loss of generality.) Therefore, the MFL
![]() $\hat f({\cdot})$
has the following form:
$\hat f({\cdot})$
has the following form:
![]() $\hat f_x(t) =f_x(0)(t)$
for
$\hat f_x(t) =f_x(0)(t)$
for
![]() $x<0$
, and
$x<0$
, and
where
![]() $\tilde f({\cdot})$
is the BMFL of the system with independent jump rate
$\tilde f({\cdot})$
is the BMFL of the system with independent jump rate
![]() $\lambda$
and synchronization rate
$\lambda$
and synchronization rate
![]() $1-\nu$
. For a sufficiently small
$1-\nu$
. For a sufficiently small
![]() $\nu>0$
, the speed
$\nu>0$
, the speed
![]() $v^{\prime}_{**}$
of
$v^{\prime}_{**}$
of
![]() $\tilde f({\cdot})$
is arbitrarily close to
$\tilde f({\cdot})$
is arbitrarily close to
![]() $v_{**}$
. (In particular, if
$v_{**}$
. (In particular, if
![]() $\alpha=0$
, then
$\alpha=0$
, then
![]() $v^{\prime}_{**}=v_{**}=\infty$
.) We conclude that any quantile
$v^{\prime}_{**}=v_{**}=\infty$
.) We conclude that any quantile
![]() $\beta > \nu$
of
$\beta > \nu$
of
![]() $f({\cdot})$
advances at average speed at least
$f({\cdot})$
advances at average speed at least
![]() $v^{\prime}_{**}$
. Since
$v^{\prime}_{**}$
. Since
![]() $\nu>0$
can be chosen arbitrarily small, any quantile
$\nu>0$
can be chosen arbitrarily small, any quantile
![]() $\beta > 0$
of
$\beta > 0$
of
![]() $f({\cdot})$
advances at average speed at least
$f({\cdot})$
advances at average speed at least
![]() $v_{**}$
.
$v_{**}$
.
20. Proof of Theorem 10
(i) Obviously, this property is a special case of the more general properties given in Proposition 2 and Theorem 8. However, we now give a simple alternative proof, which does not rely on the connection to and properties of the associated BRW, described in Theorem 7 and Proposition 1. The proof relies only on Theorem 8 and monotonicity.
By Theorem 7(ii)–(iii), the BMFL can be lower- and upper-dominated by the following traveling waves: a traveling wave with moving upper boundary with speed v’ slightly smaller that
![]() $v_*$
, and a traveling wave with moving lower boundary with speed v” slightly larger that
$v_*$
, and a traveling wave with moving lower boundary with speed v” slightly larger that
![]() $v_*$
. Since v’ and v” can be arbitrarily close to
$v_*$
. Since v’ and v” can be arbitrarily close to
![]() $v_*$
, the average speed of BMFL is
$v_*$
, the average speed of BMFL is
![]() $v_*$
. To prove that
$v_*$
. To prove that
![]() $v_*$
is a lower bound on any MFL’s average speed, the proof of Theorem 10 applies.
$v_*$
is a lower bound on any MFL’s average speed, the proof of Theorem 10 applies.
(ii) By Theorem 7(ii) there exists a TWS
![]() $\psi$
with moving left boundary and speed v’ slightly greater than
$\psi$
with moving left boundary and speed v’ slightly greater than
![]() $v(\zeta)$
. The right tail exponent of
$v(\zeta)$
. The right tail exponent of
![]() $\psi$
is slightly smaller than
$\psi$
is slightly smaller than
![]() $\zeta$
. We can always consider a version of this
$\zeta$
. We can always consider a version of this
![]() $\psi$
, shifted sufficiently far to the right, so that
$\psi$
, shifted sufficiently far to the right, so that
![]() $f(0) \preceq \psi$
. By monotonicity, MFL
$f(0) \preceq \psi$
. By monotonicity, MFL
![]() $f({\cdot})$
is dominated by the traveling wave (with moving left boundary) with speed v’, starting from
$f({\cdot})$
is dominated by the traveling wave (with moving left boundary) with speed v’, starting from
![]() $\psi$
. Therefore, the average speed of the MFL is upper-bounded by v’, which can chosen arbitrarily close to
$\psi$
. Therefore, the average speed of the MFL is upper-bounded by v’, which can chosen arbitrarily close to
![]() $v(\zeta)$
.
$v(\zeta)$
.
(iii) When
![]() $\zeta = \zeta_*$
, the claimed property follows from (i). Therefore, it suffices to consider the case
$\zeta = \zeta_*$
, the claimed property follows from (i). Therefore, it suffices to consider the case
![]() $\zeta < \zeta_*$
. Fix a small
$\zeta < \zeta_*$
. Fix a small
![]() $\nu>0$
. If
$\nu>0$
. If
![]() $\nu$
is small enough, by Theorem 7(iii) there exists a TWS
$\nu$
is small enough, by Theorem 7(iii) there exists a TWS
![]() $\psi$
for the system with synchronization rate
$\psi$
for the system with synchronization rate
![]() $\mu=1-\nu$
, with speed v’ slightly smaller than
$\mu=1-\nu$
, with speed v’ slightly smaller than
![]() $v(\zeta)$
, and with the right tail exponent of
$v(\zeta)$
, and with the right tail exponent of
![]() $\psi$
slightly larger than
$\psi$
slightly larger than
![]() $\zeta$
. Consider now the function
$\zeta$
. Consider now the function
![]() $\tilde \psi = \nu + (1-\nu) \psi$
, and consider the version of it shifted sufficiently far to the left, so that
$\tilde \psi = \nu + (1-\nu) \psi$
, and consider the version of it shifted sufficiently far to the left, so that
![]() $\tilde \psi \preceq f(0)$
. This
$\tilde \psi \preceq f(0)$
. This
![]() $\tilde \psi$
can be viewed as the initial state of an MFL for a system where the
$\tilde \psi$
can be viewed as the initial state of an MFL for a system where the
![]() $\nu n$
leftmost particles are located at
$\nu n$
leftmost particles are located at
![]() $-\infty$
and are frozen (i.e., never make any jumps); then the corresponding MFL is a traveling wave with speed v’, dominated by
$-\infty$
and are frozen (i.e., never make any jumps); then the corresponding MFL is a traveling wave with speed v’, dominated by
![]() $f({\cdot})$
. We see that any quantile
$f({\cdot})$
. We see that any quantile
![]() $\beta > \nu$
of f(t) advances at average speed at least v’. Since
$\beta > \nu$
of f(t) advances at average speed at least v’. Since
![]() $\nu$
can be arbitrarily small and v’ can be arbitrarily close to
$\nu$
can be arbitrarily small and v’ can be arbitrarily close to
![]() $v(\zeta)$
, we obtain the claim.
$v(\zeta)$
, we obtain the claim.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.