Article contents
Information ranking and power laws on trees
Published online by Cambridge University Press: 01 July 2016
Abstract
In this paper we consider the stochastic analysis of information ranking algorithms of large interconnected data sets, e.g. Google's PageRank algorithm for ranking pages on the World Wide Web. The stochastic formulation of the problem results in an equation of the form 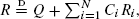 where N, Q, {Ri}i≥1, and {C, Ci}i≥1 are independent nonnegative random variables, the {C, Ci}i≥1 are identically distributed, and the {Ri}i≥1 are independent copies of
where N, Q, {Ri}i≥1, and {C, Ci}i≥1 are independent nonnegative random variables, the {C, Ci}i≥1 are identically distributed, and the {Ri}i≥1 are independent copies of 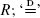 stands for equality in distribution. We study the asymptotic properties of the distribution of R that, in the context of PageRank, represents the frequencies of highly ranked pages. The preceding equation is interesting in its own right since it belongs to a more general class of weighted branching processes that have been found to be useful in the analysis of many other algorithms. Our first main result shows that if ENE[Cα] = 1, α > 0, and Q, N satisfy additional moment conditions, then R has a power law distribution of index α. This result is obtained using a new approach based on an extension of Goldie's (1991) implicit renewal theorem. Furthermore, when N is regularly varying of index α > 1, ENE[Cα] < 1, and Q, C have higher moments than α, then the distributions of R and N are tail equivalent. The latter result is derived via a novel sample path large deviation method for recursive random sums. Similarly, we characterize the situation when the distribution of R is determined by the tail of Q. The preceding approaches may be of independent interest, as they can be used for analyzing other functionals on trees. We also briefly discuss the engineering implications of our results.
stands for equality in distribution. We study the asymptotic properties of the distribution of R that, in the context of PageRank, represents the frequencies of highly ranked pages. The preceding equation is interesting in its own right since it belongs to a more general class of weighted branching processes that have been found to be useful in the analysis of many other algorithms. Our first main result shows that if ENE[Cα] = 1, α > 0, and Q, N satisfy additional moment conditions, then R has a power law distribution of index α. This result is obtained using a new approach based on an extension of Goldie's (1991) implicit renewal theorem. Furthermore, when N is regularly varying of index α > 1, ENE[Cα] < 1, and Q, C have higher moments than α, then the distributions of R and N are tail equivalent. The latter result is derived via a novel sample path large deviation method for recursive random sums. Similarly, we characterize the situation when the distribution of R is determined by the tail of Q. The preceding approaches may be of independent interest, as they can be used for analyzing other functionals on trees. We also briefly discuss the engineering implications of our results.
Keywords
MSC classification
- Type
- General Applied Probability
- Information
- Copyright
- Copyright © Applied Probability Trust 2010
References
- 36
- Cited by


