Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T20:01:23.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Heavy traffic limit theorems in fluctuation theory

Published online by Cambridge University Press:  01 July 2016

A. J. Stam
A. J. Stam*
Affiliation:
Rijksuniversiteit Groningen
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 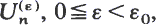be a family of random walks with 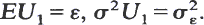For ε↓0 under certain conditions the random walk U(∊)n converges to an oscillating random walk. The ladder point distributions and expectations converge correspondingly. Let M∊ = max {U(∊)n, n ≧ 0}, v0 = min {n : U(∊)n = M∊}, v1 = max {n : U(∊)n = M∊}. The joint limiting distribution of ∊2σ∊–2v0 and ∊σ∊–2M∊ is determined. It is the same as for ∊2σ∊–2v1 and ∊σ–2∊M∊. The marginal ∊σ–2∊M∊ gives Kingman's heavy traffic theorem. Also lim ∊–1P(M∊ = 0) and lim ∊–1P(M∊ < x) are determined. Proofs are by direct comparison of corresponding probabilities for U(∊)n and for a special family of random walks related to MI/M/1 queues, using the central limit theorem.

Keywords

CONVERGENCE TO OSCILLATING RANDOM WALKSLADDER VARIABLESMAXIMUMQUEUEING
Type
Research Article
Information
Advances in Applied Probability , Volume 10 , Issue 4 , December 1978 , pp. 852 - 866
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chow, Y. S. and Lai, T. L. (1975) Some one-sided theorems on the tail distribution of sample sums with applications to the last time and largest excess of boundary crossings. Trans. Amer. Math. Soc. 208, 51–72.Google Scholar
Chung, K. L. (1968) A Course in Probability Theory, Harcourt, Brace & World, New York.Google Scholar
Cohen, J. W. (1969) The Single Server Queue. North-Holland, Amsterdam.Google Scholar
Feller, W. (1957) An Introduction to Probability Theory and its Applications. Vol. I. Wiley, New York.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. II, 2nd edn. Wiley, New York. (See also first edn, (1966).) Google Scholar
Heyde, C. C. (1975) A supplement to the strong law of large numbers. J. Appl. Prob. 12, 173–175.Google Scholar
Kingman, J. F. C. (1962a) On queues in heavy traffic. J. R. Statist. Soc. B24, 383–392.Google Scholar
Kingman, J. F. C. (1962b) Some inequalities for the queue GI/G/1. Biometrika 49, 315–324.CrossRefGoogle Scholar
Kingman, J. F. C. (1966) On the Algebra of Queues. Methuen, London.Google Scholar
Loève, M. (1963) Probability Theory, 3rd edn. Van Nostrand, Princeton N. J. Google Scholar
Müller, D. W. (1968) Verteilungs-Invarianz-prinzipien fur das starke Gesetz der groszen Zahl. Z. Wahrscheinlichkeitsth. 10, 173–192.Google Scholar
Robbins, H., Siegmund, D. and Wendel, J. (1968) The limiting distribution of the last time sn ≧ n∊. Proc. Natn. Acad. Sci. U.S.A. 61, 1228–1230.CrossRefGoogle Scholar
Roberts, G. E. and Kaufman, H. (1966) Table of Laplace Transforms. W. B. Saunders, Philadelphia.Google Scholar
Rosén, B. (1962) On the asymptotic distribution of sums of independent identically distributed random variables. Ark. Mat. 4, 323–332.CrossRefGoogle Scholar