Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T23:12:53.707Z Has data issue: false hasContentIssue false
  • English
  • Français

The geometry of random drift I. Stochastic distance and diffusion

Published online by Cambridge University Press:  01 July 2016

Peter L. Antonelli  and
Curtis Strobeck
Peter L. Antonelli
Affiliation:
University of Alberta
Curtis Strobeck*
Affiliation:
University of Sussex
*
∗Now at the University of Alberta.
Get access Rights & Permissions [Opens in a new window]

Abstract

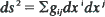A stochastic distance measure is defined for a general diffusion process on a parameter space X. This distance is defined by where (gij) is the inverse of the covariance matrix of the diffusion equation. This permits the study of the geometry associated with a diffusion equation, since the matrix (gij) is the fundamental tensor of the Riemannian space (X, gij), and of a diffusion process in terms of Brownian motion. For the diffusion equation approximation to random drift with n alleles the covariance matrix is that of a multinomial distribution. The resulting stochastic distance is equal to twice the genetic distance as defined by Cavalli-Sforza and Edwards and is a generalization of the angular transformation of Fisher to n alleles. The geometry associated with the diffusion equation for random drift with n alleles is that of a 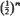part of an (n − 1)-sphere of radius two. We also show that the diffusion equation for random drift is not spherical Brownian motion, although it is approximated by it near the centroid of frequency space.

Keywords

STOCHASTIC DISTANCERANDOM GENETIC DRIFTDIFFUSION PROCESSRIEMANNIAN GEOMETRYGENERALIZED LAPLACIANSPHERICAL BROWNIAN MOTIONCHRISTOFFEL VELOCITY FIELDFISHER'S ANGULAR TRANSFORMATIONMULTINOMIAL DISTRIBUTIONMAHALANOBIS DISTANCE MEASUREEDWARDS AND CAVALLI-SFORZA DISTANCE MEASURE
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 2 , June 1977 , pp. 238 - 249
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhattacharyya, A. (1946) On a measure of divergence between two multinomial populations. Sankhyā 7, 401–406.Google Scholar
Cavalli-Sforza, L. L. and Edwards, A. W. I. (1967) Phylogenetic analysis: models and estimation procedures. Evolution 21, 550–570.Google Scholar
Douglas, J. (1927) The general geometry of path Ann. Math. (2) 29, 143–168.CrossRefGoogle Scholar
Dynkin, E. B. (1965) Markov Processes. Springer-Verlag, Berlin.Google Scholar
Dynkin, E. B. and Yushkevich, A. A. (1969) Markov Processes, Theorems and Problems. Plenum Press, New York.Google Scholar
Edwards, A. W. F. and Cavalli-Sforza, L. L. (1972) In The Assessment of Population Affinities in Man, ed. Weiner, J. S. and Huizinga, J. Clarendon Press, Oxford.Google Scholar
Eisenhart, L. P. (1926) Riemannian Geometry. Princeton University Press, Princeton, N.J. Google Scholar
Fisher, R. A. (1930) The distribution of gene ratios for rare mutations. Proc. R. Soc. Edinburgh 50, 204–219.Google Scholar
Helgason, S. (1961) Differential Geometry and Symmetric Spaces. Academic Press, New York.Google Scholar
Kelly, J. L. (1955) General Topology. Van Nostrand, Princeton, N.J. Google Scholar
Kimura, M. (1955) Random genetic drift in multi-allelic locus. Evolution 9, 419–435.Google Scholar
Kimura, M. (1964) Diffusion Models in Population Genetics. Methuen, London.CrossRefGoogle Scholar
Mahalanobis, P. C. (1936) On the generalised distance in statistics. Proc. Natn. Inst. Sci. India 2, 49–55.Google Scholar
Spain, B. (1965) Tensor Calculus. Oliver and Boyd, London.Google Scholar
Wright, S. (1945) The differential equation of the distribution of gene frequencies. Proc. Natn. Acad. Sci. U.S.A. 31, 382–389.CrossRefGoogle ScholarPubMed