Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T10:17:45.488Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalised Dickman distribution and the number of species in a negative binomial process model

Part of: Stochastic processes Distribution theory Applications

Published online by Cambridge University Press:  01 July 2021

Yuguang Ipsen ,
Ross A. Maller Open the ORCID record for Ross A. Maller [Opens in a new window]  and
Soudabeh Shemehsavar
Yuguang Ipsen*
Affiliation:
The Australian National University
Ross A. Maller*
Affiliation:
The Australian National University
Soudabeh Shemehsavar*
Affiliation:
University of Tehran
*
*Postal address: Research School of Finance, Actuarial Studies and Statistics, Australian National University, Canberra, ACT, 0200, Australia.
*Postal address: Research School of Finance, Actuarial Studies and Statistics, Australian National University, Canberra, ACT, 0200, Australia.
**Postal address: School of Mathematics, Statistics & Computer Sciences, University of Tehran. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We derive the large-sample distribution of the number of species in a version of Kingman’s Poisson–Dirichlet model constructed from an $\alpha$ -stable subordinator but with an underlying negative binomial process instead of a Poisson process. Thus it depends on parameters $\alpha\in (0,1)$ from the subordinator and 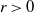$r>0$ from the negative binomial process. The large-sample distribution of the number of species is derived as sample size 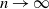$n\to\infty$ . An important component in the derivation is the introduction of a two-parameter version of the Dickman distribution, generalising the existing one-parameter version. Our analysis adds to the range of Poisson–Dirichlet-related distributions available for modeling purposes.

Keywords

Generalised Poisson–Dirichlet lawsnegative binomial point processnumber of speciesEwens sampling formulasize-biased samplinggeneralised Dickman distribution

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes 60G52: Stable processes 60G55: Point processes
Secondary: 60G57: Random measures 62E20: Asymptotic distribution theory 62P10: Applications to biology and medical sciences
Type
Original Article
Information
Advances in Applied Probability , Volume 53 , Issue 2 , June 2021 , pp. 370 - 399
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, R., Barbour, A. and Tavaré, S. (2003). Logarithmic Combinatorial Structures: a Probabilistic Approach. European Mathematical Society, Zurich.CrossRefGoogle Scholar
Arratia, R. and Baxendale, P. (2015). Bounded size bias coupling: a Gamma function bound, and universal Dickman-function behavior. Prob. Theory Relat. Fields 162, 411–429.CrossRefGoogle Scholar
Caravenna, F., Sun, R. and Zygouras, N. (2019). The Dickman subordinator, renewal theorems, and disordered systems. Electron. J. Prob. 24, paper no. 101.CrossRefGoogle Scholar
Diaconis, P. (1980). Average running time of the fast Fourier transform. J. Algorithms 1, 187–208.CrossRefGoogle Scholar
Dickman, K. (1930). On the frequency of numbers containing primes of a certain relative magnitude. Ark. Mat. Astron. Fys. 22, 1–14.Google Scholar
Ewens, W. (1972). The sampling theory of selectively neutral alleles. Theoret. Pop. Biol. 3, 87–112.CrossRefGoogle ScholarPubMed
Fill, J. A. and Huber, M. L. (2010). Perfect simulation of Vervaat perpetuities. Electron. J. Prob. 15, 96–109.CrossRefGoogle Scholar
Gil-Pelaez, J. (1951). Note on the inversion theorem. Biometrika 38, 481–482.CrossRefGoogle Scholar
Gregoire, G. (1984). Negative binomial distributions for point processes. Stoch. Process. Appl. 16, 179–188.CrossRefGoogle Scholar
Gnedenko, B. V. and Kolmogorov, A. N. (1968). Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Cambridge, MA.Google Scholar
Handa, K. (2009). The two-parameter Poisson–Dirichlet point process. Bernoulli 15, 1082–1116.CrossRefGoogle Scholar
Ipsen, Y. F. and Maller, R. A. (2017). Negative binomial construction of random discrete distributions on the infinite simplex. Theory Stoch. Process. 22, 34–46.Google Scholar
Ipsen, Y. F., Maller, R. A. and Resnick, S. (2020). Trimmed Lévy processes and their extremal components Stoch. Process. Appl. 130, 2228–2249.CrossRefGoogle Scholar
Ipsen, Y. F., Maller, R. A. and Shemehsavar, S. (2019). Limiting distributions of generalised Poisson–Dirichlet distributions based on negative binomial processes. J. Theoret. Prob. 33, 1974–2000.CrossRefGoogle Scholar
Ipsen, Y. F., Maller, R. A. and Shemehsavar, S. (2020). Size biased sampling from the Dickman subordinator. Stoch. Process. Appl. 130, 6880–6900.CrossRefGoogle Scholar
Ipsen, Y. F., Shemehsavar, S. and Maller, R. A. (2018). Species sampling models generated by negative binomial processes. Preprint. Available at https://arxiv.org/abs/1904.13046.Google Scholar
Kallenberg, O. (2002). Foundations of Modern Probability, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Kingman, J. F. C. (1975). Random discrete distributions. J. R. Statist. Soc. B 37, 1–22.Google Scholar
Mahmoud, H. M., Modarres, R. E. and Smythe, R. T. (1995). Analysis of quickselect: an algorithm for order statistics. RAIRO Inf. Théor. Appl. 29, 255–276.CrossRefGoogle Scholar
Moree, P. (2013). Nicolaas Govert de Bruijn, the enchanter of friable integers. Indag. Math. 24, 774–801.CrossRefGoogle Scholar
Penrose, M. D. and Wade, A. R. (2004). Random minimal directed spanning trees and Dickman-type distributions. Adv. Appl. Prob. 36, 691–714.CrossRefGoogle Scholar
Pinsky, R. G. (2018). On the strange domain of attraction to generalized Dickman distributions for sums of independent random variables, Electron. J. Prob. 23, 1–17.CrossRefGoogle Scholar
Pitman, J. (2006). Combinatorial Stochastic Processes. Springer, Berlin.Google Scholar
Pitman, J. and Yor, M. (1997). The two-parameter Poisson–Dirichlet distribution derived from a stable subordinator. Ann. Prob. 25, 855–900.CrossRefGoogle Scholar
R Core Team (2013). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna.Google Scholar
Sato, K. I. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar
Watterson, G. A. (1974). Models for the logarithmic species abundance distributions. Theoret. Pop. Biol. 6, 217–250.CrossRefGoogle ScholarPubMed
Watterson, G. A. (1976). The stationary distribution of the infinitely-many neutral alleles diffusion model. J. Appl. Prob. 13, 639–651.CrossRefGoogle Scholar
Watterson, G. A. and Guess, H. A. (1977). Is the most frequent allele the oldest? Theoret. Pop. Biol. 11, 141–160.Google ScholarPubMed
Zhou, M., Favaro, S. and Walker, S. G. (2017). Frequency of frequencies distributions and size-dependent exchangeable random partitions. J. Amer. Statist. Assoc. 112, 1623–1635.CrossRefGoogle Scholar