Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T06:49:14.383Z Has data issue: false hasContentIssue false
  • English
  • Français

Functional limit theorems for the euler characteristic process in the critical regime

Part of: Combinatorial probability Geometric probability and stochastic geometry Applied homological algebra and category theory Limit theorems

Published online by Cambridge University Press:  17 March 2021

Andrew M. Thomas Open the ORCID record for Andrew M. Thomas [Opens in a new window]  and
Takashi Owada
Andrew M. Thomas*
Affiliation:
Purdue University
Takashi Owada*
Affiliation:
Purdue University
*
*Postal address: Department of Statistics, Purdue University, West Lafayette, IN47907, USA. Email address: [email protected]
*Postal address: Department of Statistics, Purdue University, West Lafayette, IN47907, USA. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study presents functional limit theorems for the Euler characteristic of Vietoris–Rips complexes. The points are drawn from a nonhomogeneous Poisson process on 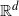$\mathbb{R}^d$ , and the connectivity radius governing the formation of simplices is taken as a function of the time parameter t, which allows us to treat the Euler characteristic as a stochastic process. The setting in which this takes place is that of the critical regime, in which the simplicial complexes are highly connected and have nontrivial topology. We establish two ‘functional-level’ limit theorems, a strong law of large numbers and a central limit theorem, for the appropriately normalized Euler characteristic process.

Keywords

Functional central limit theoremfunctional strong law of large numbersEuler characteristicgeometric simplicial complex

MSC classification

Primary: 60F17: Functional limit theorems; invariance principles
Secondary: 55U10: Simplicial sets and complexes 60C05: Combinatorial probability 60D05: Geometric probability and stochastic geometry
Type
Original Article
Information
Advances in Applied Probability , Volume 53 , Issue 1 , March 2021 , pp. 57 - 80
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. J. (2008). Some new random field tools for spatial analysis. Stoch. Environm. Res. Risk Assessment 22, 809.10.1007/s00477-008-0242-6CrossRefGoogle Scholar
Billingsley, P. (1999). Convergence of Probability Measures, 2nd edn. John Wiley, New York.10.1002/9780470316962CrossRefGoogle Scholar
Biscio, C. A. N., Chenavier, N., Hirsch, C. and Svane, A. M. (2020). Testing goodness of fit for point processes via topological data analysis. Electron. J. Statist. 14, 1024–1074.10.1214/20-EJS1683CrossRefGoogle Scholar
Bobrowski, O. and Adler, R. J. (2014). Distance functions, critical points, and the topology of random Čech complexes. Homol. Homotopy Appl. 16, 311–344.10.4310/HHA.2014.v16.n2.a18CrossRefGoogle Scholar
Bobrowski, O. and Kahle, M. (2018). Topology of random geometric complexes: a survey. J. Appl. Comput. Topol. 1, 331–364.10.1007/s41468-017-0010-0CrossRefGoogle Scholar
Bobrowski, O. and Mukherjee, S. (2015). The topology of probability distributions on manifolds. Prob. Theory Relat. Fields 161, 651–686.10.1007/s00440-014-0556-xCrossRefGoogle Scholar
Carlsson, G. (2009). Topology and data. Bull. Amer. Math. Soc. 46, 255–308.10.1090/S0273-0979-09-01249-XCrossRefGoogle Scholar
Crawford, L., Monod, A., Chen, A. X., Mukherjee, S. and Rabadán, R. (2019). Predicting clinical outcomes in glioblastoma: an application of topological and functional data analysis. J. Amer. Statist. Assoc. 115, 1139–1150.10.1080/01621459.2019.1671198CrossRefGoogle Scholar
Decreusefond, L., Ferraz, E., Randriambololona, H. and Vergne, A. (2014). Simplicial homology of random configurations. Adv. Appl. Prob. 46, 325–347.10.1239/aap/1401369697CrossRefGoogle Scholar
Edelsbrunner, H. and Harer, J. (2010). Computational Topology: an Introduction. American Mathematical Society, Providence, RI.Google Scholar
Goel, A., Trinh, K. D. and Tsunoda, K. (2019). Strong law of large numbers for Betti numbers in the thermodynamic regime. J. Statist. Phys. 174, 865–892.10.1007/s10955-018-2201-zCrossRefGoogle Scholar
Hatcher, A. (2002). Algebraic Topology. Cambridge University Press.Google Scholar
Hiraoka, Y., Shirai, T. and Trinh, K. D. (2018). Limit theorems for persistence diagrams. Ann. Appl. Prob. 28, 2740–2780.10.1214/17-AAP1371CrossRefGoogle Scholar
Hug, D., Last, G. and Schulte, M. (2016). Second-order properties and central limit theorems for geometric functionals of Boolean models. Ann. Prob. 26, 73–135.10.1214/14-AAP1086CrossRefGoogle Scholar
Kahle, M. (2011). Random geometric complexes. Discrete Computat. Geom. 45, 553–573.10.1007/s00454-010-9319-3CrossRefGoogle Scholar
Kahle, M. and Meckes, E. (2013). Limit theorems for Betti numbers of random simplicial complexes. Homol. Homotopy Appl. 15, 343–374.10.4310/HHA.2013.v15.n1.a17CrossRefGoogle Scholar
Karatzas, I. and Shreve, S. E. (1991). Brownian Motion and Stochastic Calculus. Springer, New York.Google Scholar
Owada, T. (2017). Functional central limit theorem for subgraph counting processes. Electron. J. Prob. 22, 38 pp.10.1214/17-EJP30CrossRefGoogle Scholar
Owada, T. (2019). Topological crackle of heavy-tailed moving average processes. Stoch. Process. Appl. 129, 4965–4997.10.1016/j.spa.2018.12.017CrossRefGoogle Scholar
Owada, T. and Thomas, A. M. (2020). Limit theorems for process-level Betti numbers for sparse and critical regimes. Adv. Appl. Prob. 52, 1–31.10.1017/apr.2019.50CrossRefGoogle Scholar
Penrose, M. D. (2000). Central limit theorems for k-nearest neighbour distances. Stoch. Process. Appl. 85, 295–320.10.1016/S0304-4149(99)00080-0CrossRefGoogle Scholar
Penrose, M. D. (2003). Random Geometric Graphs. Oxford University Press.10.1093/acprof:oso/9780198506263.001.0001CrossRefGoogle Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, New York.10.1007/978-3-540-78859-1CrossRefGoogle Scholar
Whitt, W. (2002). Stochastic-Process Limits: an Introduction to Stochastic-Process Limits and Their Application to Queues. Springer, New York.10.1007/b97479CrossRefGoogle Scholar
Yogeshwaran, D., Subag, E. and Adler, R. J. (2017). Random geometric complexes in the thermodynamic regime. Prob. Theory Relat. Fields 167, 107–142.10.1007/s00440-015-0678-9CrossRefGoogle Scholar