Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rahimov, I.
2008.
Asymptotically Normal Estimators for the Offspring Mean in the Branching Process with Immigration.
Communications in Statistics - Theory and Methods,
Vol. 38,
Issue. 1,
p.
13.
Rahimov, I.
2008.
Asymptotic distribution of the CLSE in a critical process with immigration.
Stochastic Processes and their Applications,
Vol. 118,
Issue. 10,
p.
1892.
Rahimov, I.
2009.
Bootstrap of the offspring mean in the critical process with a non-stationary immigration.
Stochastic Processes and their Applications,
Vol. 119,
Issue. 11,
p.
3939.
Rahimov, I.
2009.
Asymptotic distributions for weighted estimators of the offspring mean in a branching process.
TEST,
Vol. 18,
Issue. 3,
p.
568.
Ispány, Márton
and
Pap, Gyula
2010.
Workshop on Branching Processes and Their Applications.
Vol. 197,
Issue. ,
p.
135.
Rahimov, Ibrahim
2010.
Workshop on Branching Processes and Their Applications.
Vol. 197,
Issue. ,
p.
121.
Rahimov, I.
and
Omar, M. H.
2011.
Validity of the bootstrap in the critical process with a non-stationary immigration.
Journal of Nonparametric Statistics,
Vol. 23,
Issue. 1,
p.
1.
Rahimov, I.
2011.
Estimation of the offspring mean in a supercritical branching process with non-stationary immigration.
Statistics & Probability Letters,
Vol. 81,
Issue. 8,
p.
907.
RAHIMOV, IBRAHIM
and
YANEV, GEORGE P.
2012.
Variance Estimators in Critical Branching Processes With Non-Homogeneous Immigration.
Mathematical Population Studies,
Vol. 19,
Issue. 4,
p.
188.
Rahimov, I.
2012.
Conditional Least Squares Estimators for the Offspring Mean in a Subcritical Branching Process with Immigration.
Communications in Statistics - Theory and Methods,
Vol. 41,
Issue. 12,
p.
2096.
Khusanbaev, Ya. M.
2013.
On the Asymptotic Behavior of a Subcritical Branching Process with Immigration.
Ukrainian Mathematical Journal,
Vol. 65,
Issue. 6,
p.
928.
Guo, Hongsong
and
Zhang, Mei
2014.
A fluctuation limit theorem for a critical branching process with dependent immigration.
Statistics & Probability Letters,
Vol. 94,
Issue. ,
p.
29.
Khusanbaev, Yakubdzhan Mukhamadzhanovich
2016.
Об асимптотике ветвящихся процессов с иммиграцией.
Дискретная математика,
Vol. 28,
Issue. 1,
p.
113.
Khusanbaev, Yakubdzhan M.
2017.
On asymptotics of branching processes with immigration.
Discrete Mathematics and Applications,
Vol. 27,
Issue. 2,
Barczy, Mátyás
Bezdány, Dániel
and
Pap, Gyula
2021.
A note on asymptotic behavior of critical Galton–Watson processes with immigration.
Involve, a Journal of Mathematics,
Vol. 14,
Issue. 5,
p.
871.
Rahimov, Ibrahim
2021.
Homogeneous Branching Processes with Non-Homogeneous Immigration.
Stochastics and Quality Control,
Vol. 36,
Issue. 2,
p.
165.
Chen, Longyu
Liu, Xiaohui
Peng, Liang
and
Zhu, Fukang
2024.
Unified inference for an integer-valued AR(1) model.
Communications in Statistics - Theory and Methods,
p.
1.
Barreto‐Souza, Wagner
and
Chan, Ngai Hang
2024.
Nearly unstable integer‐valued ARCH process and unit root testing.
Scandinavian Journal of Statistics,
Vol. 51,
Issue. 1,
p.
402.
Sharipov, Sadillo Olimjonovich
2024.
Функциональная предельная теорема для критического ветвящегося процесса со слабо зависимой иммиграцией.
Дискретная математика,
Vol. 36,
Issue. 1,
p.
136.
Rahimov, I.
and
Sharipov, S.O.
2024.
On deterministic approximation for nearly critical branching processes with dependent immigration.
Statistics & Probability Letters,
Vol. 208,
Issue. ,
p.
110031.
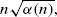 where α(n) denotes the mean number of immigrating individuals in the nth generation.
where α(n) denotes the mean number of immigrating individuals in the nth generation.

