Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Buaic, Ana
Gupta, Varun
and
Mairesse, Jean
2010.
Stability of the bipartite matching model.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 38,
Issue. 2,
p.
6.
Adan, Ivo
Hurkens, Cor
and
Weiss, Gideon
2010.
A REVERSIBLE ERLANG LOSS SYSTEM WITH MULTITYPE CUSTOMERS AND MULTITYPE SERVERS.
Probability in the Engineering and Informational Sciences,
Vol. 24,
Issue. 4,
p.
535.
Adan, Ivo
and
Weiss, Gideon
2012.
Exact FCFS Matching Rates for Two Infinite Multitype Sequences.
Operations Research,
Vol. 60,
Issue. 2,
p.
475.
Adan, Ivo
and
Weiss, Gideon
2012.
A LOSS SYSTEM WITH SKILL-BASED SERVERS UNDER ASSIGN TO LONGEST IDLE SERVER POLICY.
Probability in the Engineering and Informational Sciences,
Vol. 26,
Issue. 3,
p.
307.
Bušić, Ana
Gupta, Varun
and
Mairesse, Jean
2013.
Stability of the Bipartite Matching Model.
Advances in Applied Probability,
Vol. 45,
Issue. 2,
p.
351.
Adan, Ivo
Boon, Marko
and
Weiss, Gideon
2013.
Design and evaluation of overloaded service systems with skill based routing, under FCFS policies.
Performance Evaluation,
Vol. 70,
Issue. 10,
p.
873.
Adan, Ivo
Boon, Marko
Bušić, Ana
Mairesse, Jean
and
Weiss, Gideon
2014.
Queues with skill based parallel servers and a FCFS infinite matching model.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 41,
Issue. 3,
p.
22.
Adan, Ivo
and
Weiss, Gideon
2014.
A Skill Based Parallel Service System Under FCFS-ALIS — Steady State, Overloads, and Abandonments.
Stochastic Systems,
Vol. 4,
Issue. 1,
p.
250.
Buýić, Ana
and
Meyn, Sean
2015.
Approximate optimality with bounded regret in dynamic matching models.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 43,
Issue. 2,
p.
75.
Büke, Burak
and
Chen, Hanyi
2015.
Stabilizing policies for probabilistic matching systems.
Queueing Systems,
Vol. 80,
Issue. 1-2,
p.
35.
Ding, Yichuan
McCormick, S. Thomas
and
Nagarajan, Mahesh
2016.
A Fluid Model for an Overloaded Bipartite Queueing System with Heterogeneous Matching Utility.
SSRN Electronic Journal ,
Bonald, Thomas
and
Comte, Céline
2017.
Balanced fair resource sharing in computer clusters.
Performance Evaluation,
Vol. 116,
Issue. ,
p.
70.
Leshno, Jacob D.
2017.
Dynamic Matching in Overloaded Waiting Lists.
SSRN Electronic Journal ,
Adan, Ivo
Righter, Rhonda
and
Weiss, Gideon
2017.
FCFS Parallel Service Systems and Matching Models.
p.
106.
Anderson, Ross
Ashlagi, Itai
Gamarnik, David
and
Kanoria, Yash
2017.
Efficient Dynamic Barter Exchange.
Operations Research,
Vol. 65,
Issue. 6,
p.
1446.
Fazel-Zarandi, Mohammad M.
and
Kaplan, Edward H.
2018.
Approximating the First-Come, First-Served Stochastic Matching Model with Ohm’s Law.
Operations Research,
Vol. 66,
Issue. 5,
p.
1423.
Adan, Ivo
Kleiner, Igor
Righter, Rhonda
and
Weiss, Gideon
2018.
FCFS parallel service systems and matching models.
Performance Evaluation,
Vol. 127-128,
Issue. ,
p.
253.
Adan, Ivo
Bušić, Ana
Mairesse, Jean
and
Weiss, Gideon
2018.
Reversibility and Further Properties of FCFS Infinite Bipartite Matching.
Mathematics of Operations Research,
Vol. 43,
Issue. 2,
p.
598.
Adan, Ivo J.B.F.
Boon, Marko A.A.
and
Weiss, Gideon
2019.
Design heuristic for parallel many server systems.
European Journal of Operational Research,
Vol. 273,
Issue. 1,
p.
259.
Aouad, Ali
and
Saritac, Omer
2019.
Dynamic Stochastic Matching Under Limited Time.
SSRN Electronic Journal ,
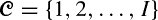 and an infinite sequence of servers of types
and an infinite sequence of servers of types 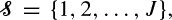 where a server of type j can serve a subset of customer types C(j) and where a customer of type i can be served by a subset of server types S(i). We assume that the types of customers and servers in the infinite sequences are random, independent, and identically distributed, and that customers and servers are matched according to their order in the sequence, on a first-come–first-served (FCFS) basis. We investigate this process of infinite bipartite matching. In particular, we are interested in the rate ri,j that customers of type i are assigned to servers of type j. We present a countable state Markov chain to describe this process, and for some previously unsolved instances, we prove ergodicity and existence of limiting rates, and calculate ri,j.
where a server of type j can serve a subset of customer types C(j) and where a customer of type i can be served by a subset of server types S(i). We assume that the types of customers and servers in the infinite sequences are random, independent, and identically distributed, and that customers and servers are matched according to their order in the sequence, on a first-come–first-served (FCFS) basis. We investigate this process of infinite bipartite matching. In particular, we are interested in the rate ri,j that customers of type i are assigned to servers of type j. We present a countable state Markov chain to describe this process, and for some previously unsolved instances, we prove ergodicity and existence of limiting rates, and calculate ri,j.

