Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T08:31:02.565Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact values and sharp estimates for the total variation distance between binomial and Poisson distributions

Part of: Distribution theory - Probability Distribution theory

Published online by Cambridge University Press:  01 July 2016

José A. Adell ,
José M. Anoz  and
Alberto Lekuona
José A. Adell*
Affiliation:
Universidad de Zaragoza
José M. Anoz*
Affiliation:
Universidad de Zaragoza
Alberto Lekuona*
Affiliation:
Universidad de Zaragoza
*
∗ Postal address: Departamento de Métodos Estadísticos, Facultad de Ciencias, Universidad de Zaragoza, 50009 Zaragoza, Spain.
∗ Postal address: Departamento de Métodos Estadísticos, Facultad de Ciencias, Universidad de Zaragoza, 50009 Zaragoza, Spain.
∗ Postal address: Departamento de Métodos Estadísticos, Facultad de Ciencias, Universidad de Zaragoza, 50009 Zaragoza, Spain.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present a method to obtain both exact values and sharp estimates for the total variation distance between binomial and Poisson distributions with the same mean λ. We give a simple efficient algorithm, whose complexity order is 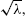to compute exact values. Such an algorithm can be further simplified for moderate sample sizes n, provided that λ is neither close to 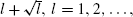from the left nor close to 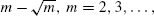from the right. Sharp estimates, better than other known estimates in the literature, are also provided. The 0s of the second Krawtchouk and Charlier polynomials play a fundamental role.

Keywords

Poisson approximationbinomial distributiontotal variation distanceKrawtchouk polynomialCharlier polynomial

MSC classification

Primary: 62E17: Approximations to distributions (nonasymptotic)
Secondary: 60E15: Inequalities; stochastic orderings
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 40 , Issue 4 , December 2008 , pp. 1033 - 1047
Copyright
Copyright © Applied Probability Trust 2008 

References

Adell, J. A. (2008). A differential calculus for linear operators represented by stochastic processes. Preprint. Available at http://www.unizar.es/galdeano/preprints/lista.html.Google Scholar
Adell, J. A. and Anoz, J. M. (2008). Signed binomial approximation of binomial mixtures via differential calculus for linear operators. J. Statist. Planning Infer. 138, 3687–3698.Google Scholar
Adell, J. A. and Lekuona, A. (2000). Taylor's formula and preservation of generalized convexity for positive linear operators. J. Appl. Prob. 37, 765–777.Google Scholar
Adell, J. A. and Lekuona, A. (2005). Sharp estimates in signed Poisson approximation of Poisson mixtures. Bernoulli 11, 47–65.Google Scholar
Adell, J. A. and Pérez-Palomares, A. (1999). Stochastic orders in preservation properties by Bernstein-type operators. Adv. Appl. Prob. 31, 492–509.CrossRefGoogle Scholar
Barbour, A. D. and Hall, P. (1984). On the rate of Poisson convergence. Math. Proc. Camb. Phil. Soc. 95, 473–480.Google Scholar
Barbour, A. D. and Xia, A. (2000). Estimating Stein's constants for compound Poisson approximation. Bernoulli 6, 581–590.Google Scholar
Barbour, A. D., Holst, L. and Janson, S. (1992). Poisson Approximation (Oxford Stud. Prob. 2). Clarendon Press, Oxford.Google Scholar
Borisov, I. S. and Ruzankin, P. S. (2002). Poisson approximation for expectations of unbounded functions of independent random variables. Ann. Prob. 30, 1657–1680.CrossRefGoogle Scholar
Chen, L. H. Y. (1975). Poisson approximation for dependent trials. Ann. Prob. 3, 534–545.Google Scholar
Chihara, T. S. (1978). An Introduction to Orthogonal Polynomials. Gordon and Breach, New York.Google Scholar
Deheuvels, P. and Pfeifer, D. (1986). A semigroup approach to Poisson approximation. Ann. Prob. 14, 663–676.Google Scholar
Deheuvels, P., Pfeifer, D. and Puri, M. L. (1989). A new semigroup technique in Poisson approximation. Semigroup Forum 38, 189–201.Google Scholar
Kennedy, J. E. and Quine, M. P. (1989). The total variation distance between the binomial and Poisson distributions. Ann. Prob. 17, 396–400.Google Scholar
Kerstan, J. (1964). Verallgemeinerung eines Satzes von Prochorow und Le Cam. Z. Wahrscheinlichkeitsth. 2, 173–179.Google Scholar
Le Cam, L. (1960). An approximation theorem for the Poisson binomial distribution. Pacific J. Math. 10, 1181–1197.Google Scholar
Prohorov, Y. V. (1953). Asymptotic behavior of the binomial distribution. Uspehi Matem. Nauk 8, 135–142.Google Scholar
Roos, B. (1999). Asymptotic and sharp bounds in the Poisson approximation to the Poisson-binomial distribution. Bernoulli 5, 1021–1034.Google Scholar
Roos, B. (2001). Sharp constants in the Poisson approximation. Statist. Prob. Lett. 52, 155–168.Google Scholar
Schoutens, W. (2000). Stochastic Processes and Orthogonal Polynomials (Lecture Notes Statist. 146). Springer, New York.CrossRefGoogle Scholar
Weinberg, G. V. (2000). Stein factor bounds for random variables. J. Appl. Prob. 37, 1181–1187.CrossRefGoogle Scholar
Xia, A. (1999). A probabilistic proof of Stein's factors. J. Appl. Prob. 36, 287–290.Google Scholar