Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T07:02:43.225Z Has data issue: false hasContentIssue false
  • English
  • Français

The diameter of KPKVB random graphs

Part of: Equilibrium statistical mechanics Geometric probability and stochastic geometry Graph theory

Published online by Cambridge University Press:  07 August 2019

Tobias Müller  and
Merlijn Staps
Tobias Müller*
Affiliation:
Utrecht University
Merlijn Staps*
Affiliation:
Utrecht University
*
*Current address: Bernoulli Institute, University of Groningen, Nijenborgh 9, 9747 AG Groningen, The Netherlands. Email address: [email protected]
**Current address: Department of Ecology and Evolutionary Biology, Princeton University, Princeton, NJ 08544, USA. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a random graph model that was recently proposed as a model for complex networks by Krioukov et al. (2010). In this model, nodes are chosen randomly inside a disk in the hyperbolic plane and two nodes are connected if they are at most a certain hyperbolic distance from each other. It has previously been shown that this model has various properties associated with complex networks, including a power-law degree distribution and a strictly positive clustering coefficient. 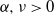The model is specified using three parameters: the number of nodes N, which we think of as going to infinity, and $\alpha, \nu > 0$, which we think of as constant. Roughly speaking, $\alpha$ controls the power-law exponent of the degree sequence and $\nu$ the average degree. Earlier work of Kiwi and Mitsche (2015) has shown that, when 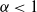$\alpha \lt 1$ (which corresponds to the exponent of the power law degree sequence being 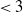$\lt 3$), the diameter of the largest component is asymptotically almost surely (a.a.s.) at most polylogarithmic in N. Friedrich and Krohmer (2015) showed it was a.a.s. 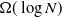$\Omega(\log N)$ and improved the exponent of the polynomial in 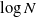$\log N$ in the upper bound. Here we show the maximum diameter over all components is a.a.s. 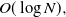$O(\log N),$ thus giving a bound that is tight up to a multiplicative constant.

Keywords

Random graphcomplex networkhyperbolic planegraph diameter

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C82: Small world graphs, complex networks 05C12: Distance in graphs 60D05: Geometric probability and stochastic geometry 82B43: Percolation
Type
Original Article
Information
Advances in Applied Probability , Volume 51 , Issue 2 , June 2019 , pp. 358 - 377
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported in part by the Netherlands Organisation for Scientific Research (NWO) under project numbers 612.001.409 and 639.032.529.

This paper is the result of this author’s MSc thesis [16], carried out at Utrecht University under the supervision of the first author.

References

Abdullah, M. A., Bode, M. and Fountoulakis, N. (2015). Typical distances in a geometric model for complex networks. Preprint. Available at https://arxiv.org/abs/1506.07811v1https://arxiv.org/abs/1506.07811v1.Google Scholar
Bläsius, T., Friedrich, T., and Krohmer, A.. (2016). Hyperbolic random graphs: Separators and treewidth. In 24th Annual European Symposium on Algorithms, eds Sankowski, P. and Zaroliagis, C. D., Dagstuhl, Schloss, Leibniz-Zentrum fuer Informatik, Wadern, 18pp.Google Scholar
Bläsius, T., Friedrich, T., Krohmer, A., and Laue, S.. (2016). Efficient embedding of scale-free graphs in the hyperbolic plane. In 24th Annual European Symposium on Algorithms, eds Sankowski, P. and Zaroliagis, C. D., Dagstuhl, Schloss, Leibniz-Zentrum fuer Informatik, Wadern, 18pp.Google Scholar
Bode, M., Fountoulakis, N., and Müller, T.. (2015). On the largest component of a hyperbolic model of complex networks. Electron. J. Combinatorics 22, 46pp.Google Scholar
Bode, M., Fountoulakis, N., and Müller, T.. (2016). The probability of connectivity in a hyperbolic model of complex networks. Random Structures Algorithms, 49, 65–94.CrossRefGoogle Scholar
Boguñá, M., Papadopoulos, F., and Krioukov, D.. (2010). Sustaining the internet with hyperbolic mapping. Nature Commun. 1, 8pp.CrossRefGoogle Scholar
Fountoulakis, N. and Müller, T.. (2018). Law of large numbers for the largest component in a hyperbolic model of complex networks. Ann. Appl. Prob. 28, 607–650.CrossRefGoogle Scholar
Friedrich, T. and Krohmer, A.. (2015). Cliques in hyperbolic random graphs. In IEEE Conference on Computer Communications (INFOCOM), IEEE, Piscataway, NJ, pp. 1544–1552.CrossRefGoogle Scholar
Friedrich, T. and Krohmer, A.. (2015). On the diameter of hyperbolic random graphs. In Automata, Languages, and Programming. Part II, ICALP 2015, eds Halldórsson, M. M. et al., Springer, Heidelberg, pp. 614–625.CrossRefGoogle Scholar
Gugelmann, L., Panagiotou, K., and Peter, U.. (2012). Random hyperbolic graphs: Degree sequence and clustering. In Automata, Languages, and Programming. Part II, ICALP 2012, eds Czumaj, A. et al., Springer, Heidelberg, pp. 573–585.CrossRefGoogle Scholar
Kesten, H.. (1982). Percolation Theory for Mathematicians. Birkhäuser, Boston.CrossRefGoogle Scholar
Kingman, J. F. C.. (1993). Poisson Processes (Oxford Stud. Prob. 3). Clarendon Press, New York.Google Scholar
Kiwi, M. and Mitsche, D.. (2015). A bound for the diameter of random hyperbolic graphs. In Proceedings of the Twelfth Workshop on Analytic Algorithmics and Combinatorics (ANALCO), SIAM, Philadelphia, pp. 26–39.CrossRefGoogle Scholar
Kiwi, M. and Mitsche, D.. (2018). Spectral gap of random hyperbolic graphs and related parameters. Ann. Appl. Prob. 28, 941–989.CrossRefGoogle Scholar
Krioukov, D. et al. (2010). Hyperbolic geometry of complex networks. Phys. Rev. E, 82, 18pp.CrossRefGoogle Scholar
Staps, M.. The diameter of hyperbolic random graphs. (2017). Master’s Thesis, Utrecht University. Available at http://studenttheses.library.uu.nl/search.php?language=enhttp://studenttheses.library.uu.nl/search.php?language=en.Google Scholar
Stillwell, J.. (1992). Geometry of Surfaces. Universitext, Springer, New York.Google Scholar