Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T03:28:03.848Z Has data issue: false hasContentIssue false
  • English
  • Français

A counterexample to a conjecture of J. M. Hammersley and D. J. A. Welsh concerning first-passage percolation

Published online by Cambridge University Press:  01 July 2016

J. Van Den Berg
J. Van Den Berg*
Affiliation:
Delft University of Technology
*
∗Postal address: Department of Mathematics, Delft University of Technology, Julianalaan 132, 2628 BL Delft, The Netherlands.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider first-passage percolation on the square lattice. Hammersley and Welsh, who introduced the subject in 1965, conjectured that the expected minimum travel time from (0, 0) to (n, 0) along paths contained in the cylinder 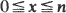is always non-decreasing in n. However, when the bonds have time-coordinate 1 with probability p and 0 with probability 1 – p (0 < P < 1), then, for p sufficiently small, we get a counterexample.

Keywords

EXPECTED CYLINDER TIMES
Type
Letters to the Editor
Information
Advances in Applied Probability , Volume 15 , Issue 2 , June 1983 , pp. 465 - 467
Copyright
Copyright © Applied Probability Trust 1983 

Footnotes

Investigations supported by the Netherlands Foundation for Mathematics SMC with financial aid from the Netherlands Organization for the Advancement of Pure Research (ZWO).

References

Hammersley, J. M. and Welsh, D. J. A. (1965) in Bernoulli Bayes Laplace Anniversary Volume, ed. Neyman, J. and Le Cam, L. M., Springer-Verlag, Berlin, 61–110.Google Scholar
Smythe, R. T. and Wierman, J. C. (1978) First-Passage Percolation on the Square Lattice. Lecture Notes in Mathematics 671, Springer-Verlag, Berlin.Google Scholar
Whitney, H. (1933) Planar graphs. Fundamenta Math. 21, 73–84.Google Scholar