Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T07:24:41.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Correlations in bivariate point processes: some biological applications

Published online by Cambridge University Press:  01 July 2016

Guillermo Ayala  and
Amelia Simó
Guillermo Ayala
Affiliation:
Universitat de Valencia
Amelia Simó
Affiliation:
Universitat Jaume I
Get access Rights & Permissions [Opens in a new window]

Extract

Let (Φ1 Φ2) be a bivariate point process. Let 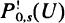be the probability that (Φ1 Φ2) - (0, s) (the process without the 0 and s points) verify U when we have a point of <1>1 in the origin and a point of Φ2 in s. This is the reduced cross Palm distribution. Some correlation measures for bivariate point processes based on this reduced cross Palm distribution are proposed. Their estimators and expressions under the independence and the random labelling hypothesis are considered. The differences and improvements with respect to the cross intensity function and its integrated version, the cross function (Stoyan et al. 1987), are studied. Some Monte Carlo tests for testing the independence and the random labelling hypothesis are proposed. They are applied to real bivariate point patterns: positions of hickories and maples in the Lansing Woods (Diggle 1983) and cases and controls of childhood leukaemia and lymphoma in North Humberside (Cuzick and Edwards 1990).

Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 28 , Issue 2 , June 1996 , pp. 330
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cuzick, J. and Edwards, R. (1990) Spatial clustering for inhomogenous populations. J. R. Statist. Soc. B 52, 73–104.Google Scholar
Diggle, P. (1983) Statistical Analysis of Spatial Point Patterns. Academic Press, London.Google Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1987) Stochastic Geometry and its Applications. Wiley, Berlin.Google Scholar