Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T04:49:03.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison of optimal value and constrained maxima expectations for independent random variables

Published online by Cambridge University Press:  01 July 2016

Robert P. Kertz
Robert P. Kertz*
Affiliation:
Georgia Institute of Technology
*
∗Postal address: School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

For all uniformly bounded sequences of independent random variables X1, X2, ···, a complete comparison is made between the optimal value V(X1, X2, ···) = sup {EXt:t is an (a.e.) finite stop rule for X1,X2, ···} and 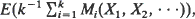, where Mi(X1,X2, ···) is the ith largest order statistic for X1, X2, ··· In particular, for k> 1, the set of ordered pairs {(x, y):x = V(X1, X2, ···) and 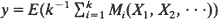for some independent random variables X1, X2, ··· taking values in [0, 1]} is precisely the set 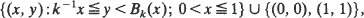, where Bk(0) = 0, Bk(1) = 1, and for 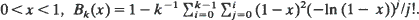The result yields sharp, universal inequalities for independent random variables comparing two choice mechanisms, the mortal&s value of the game V(X1, X2, ···) and the prophet&s constrained maxima expectation of the game 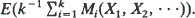. Techniques of proof include probability- and convexity-based reductions; calculus-based, multivariate, extremal problem analysis; and limit theorems of Poisson-approximation type. Precise results are also given for finite sequences of independent random variables.

Keywords

SHARP INEQUALITIES FOR INDEPENDENT PROCESSESOPTIMAL STOPPINGPROPHET REGIONSORDER STATISTICSPOISSON APPROXIMATIONEXTREMAL DISTRIBUTIONS
Type
Research Article
Information
Advances in Applied Probability , Volume 18 , Issue 2 , June 1986 , pp. 311 - 340
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported in part by National Science Foundation Grant DMS-84-01604.

References

1. Breiman, L. (1968) Probability. Addison-Wesley, Reading, Mass.Google Scholar
2. Chow, Y. S., Robbins, H., and Siegmund, D. (1971) Great Expectations: The Theory of Optimal Stopping. Houghton Mifflin, Boston.Google Scholar
3. Cox, D. C. and Kertz, R. P. (1984) Prophet regions and sharp inequalities for pth absolute moments of martingales. J. Multivariate Anal. 20, 169–179.Google Scholar
4. Cox, D. C. and Kertz, R. P. (1985) Common strict character of some sharp infinite-sequence martingale inequalities. Stoch. Proc. Appl. To appear.CrossRefGoogle Scholar
5. Dubins, L. E. (1962) Rises and upcrossings of nonnegative martingales. Illinois J. Math. 6, 226–241.CrossRefGoogle Scholar
6. Dubins, L. E. and Pitman, J. (1980) A maximal inequality for skew fields. Z. Wahrscheinlichkeitsth. 52, 219–227.CrossRefGoogle Scholar
7. Hildenbrand, W. (1974) Core and Equilibria of a Large Economy. Princeton University Press, Princeton, NJ.Google Scholar
8. Hill, T. (1983) Prophet inequalities and order selection in optimal stopping problems. Proc. Amer. Math. Soc. 88, 131–137.Google Scholar
9. Hill, T. and Kertz, R. P. (1981) Ratio comparisons of supremum and stop rule expectations. Z. Wahrscheinlichkeitsth. 56, 283–285.CrossRefGoogle Scholar
10. Hill, T. and Kertz, R. P. (1981) Additive comparisons of stop rule and supremum expectations of uniformly bounded independent random variables. Proc. Amer. Math. Soc. 83, 582–585.CrossRefGoogle Scholar
11. Hill, T. and Kertz, R. P. (1982) Comparisons of stop rule and supremum expectations of i.i.d. random variables. Ann. Prob. 10, 336–345.Google Scholar
12. Kennedy, D. P. (1985) Optimal stopping of independent random variables and maximizing prophets. Ann. Prob. 13, 566–571.Google Scholar
13. Kertz, R. P. (1984) Stop rule and supremum expectations of i.i.d. random variables: a complete comparison by conjugate duality. J. Multivariate Anal. To appear.Google Scholar
14. Krengel, U. and Sucheston, L. (1977) Semiamarts and finite values. Bull. Amer. Math. Soc. 83, 745–747.Google Scholar
15. Krengel, U. and Sucheston, L. (1978) On semiamarts, amarts, and processes with finite value. Adv. Prob. Related Topics 4, 197–266.Google Scholar
16. Leadbetter, M. R., Lindgren, G., and Rootzen, H. (1983) Extremes and Related Properties of Random Sequences and Processes. Springer-Verlag, New York.CrossRefGoogle Scholar
17. Rockafeller, R. T. (1970) Convex Analysis. Princeton University Press, Princeton, NJ.CrossRefGoogle Scholar