Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T07:03:36.306Z Has data issue: false hasContentIssue false
  • English
  • Français

Classes of probability density functions having Laplace transforms with negative zeros and poles

Published online by Cambridge University Press:  01 July 2016

Ushio Sumita  and
Yasushi Masuda
Ushio Sumita*
Affiliation:
University of Rochester
Yasushi Masuda*
Affiliation:
University of Rochester
*
∗Postal address: William E. Simon Graduate School of Business Administration, University of Rochester, Rochester, NY 14627, USA.
∗Postal address: William E. Simon Graduate School of Business Administration, University of Rochester, Rochester, NY 14627, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a class of functions on [0,∞), denoted by Ω, having Laplace transforms with only negative zeros and poles. Of special interest is the class Ω+ of probability density functions in Ω. Simple and useful conditions are given for necessity and sufficiency of f ∊ Ω to be in Ω+. 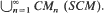The class Ω+ contains many classes of great importance such as mixtures of n independent exponential random variables (CMn), sums of n independent exponential random variables (PF∗n), sums of two independent random variables, one in CMr and the other in PF∗1 (CMPFn with n = r + l) and sums of independent random variables in CMn(SCM). Characterization theorems for these classes are given in terms of zeros and poles of Laplace transforms. The prevalence of these classes in applied probability models of practical importance is demonstrated. In particular, sufficient conditions are given for complete monotonicity and unimodality of modified renewal densities.

Keywords

RATIONAL LAPLACE TRANSFORMSSUMS AND MIXTURES OF EXPONENTIAL RANDOM VARIABLESCHARACTERIZATION THEOREMSCOMPLETE MONOTONICITYUNIMODALITYMODIFIED RENEWAL DENSITIESBIRTH-DEATH PROCESSES
Type
Research Article
Information
Advances in Applied Probability , Volume 19 , Issue 3 , September 1987 , pp. 632 - 651
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper is dedicated with respect to Julian Keilson in honor of his 60th birthday.

References

1. Bondesson, L. (1981) Classes of infinitely divisible distributions and densities. Z. Wahrscheinlichkeitsth. 57, 39–71.CrossRefGoogle Scholar
2. Bondesson, L. (1982) Correction and addendum. Z. Wahrscheinlichkeitsth. 59, 277.Google Scholar
3. Cox, D. R. (1955) A use of complex probabilities in the theory of stochastic processes. Proc. Camb. Phil. Soc. 51, 313–319.Google Scholar
4. Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
5. Gaver, D. P. (1962) A waiting line with interrupted service, including priorities. J.R. Statist. Soc. B 24, 73–90.Google Scholar
6. Karlin, S. (1968) Total Positivity. Stanford University Press, Stanford, CA.Google Scholar
7. Karlin, S. and Mcgregor, J. L. (1957) The differential equations of birth-death processes, and the Stieltjes moment problem. Trans. Amer. Math. Soc. 85, 489–546.Google Scholar
8. Karlin, S. and Mcgregor, J. L. (1957) The classification of birth-death processes. Trans. Amer. Math. Soc. 86, 366–400.Google Scholar
9. Karlin, S. and Mcgregor, J. L. (1959) A characterization of birth and death processes. Proc. Nat. Acad. Sci. U.S.A. 45, 375–379.Google Scholar
10. Keilson, J. (1962) Queue subject to service interruption. Ann. Math. Statist. 33, 1314–1322.Google Scholar
11. Keilson, J. (1964) A review of transient behavior on regular diffusion and birth-death processes Part I. J. Appl. Prob. 1, 247–266.CrossRefGoogle Scholar
12. Keilson, J. (1965) A review of transient behavior on regular diffusion and birth-death processes Part II. J. Appl. Prob. 2, 405–428.CrossRefGoogle Scholar
13. Keilson, J. (1966) A technique for discussing the passage time distribution to stable systems. J. R. Statist. Soc. B 28, 477–486.Google Scholar
14. Keilson, J. (1971) Log-concavity and log-convexity in passage time densities of diffusion and birth-death processes. J. Appl. Prob. 8, 391–398.Google Scholar
15. Keilson, J. (1978) Exponential spectra as a tool for the study of server-systems with several classes of customers. J. Appl. Prob. 15, 162–170.Google Scholar
16. Keilson, J. (1979) Markov Chain Models–Rarity and Exponentiality. Applied Mathematical Science Series, 28, Springer-Verlag, New York.Google Scholar
17. Keilson, J. (1981) On the unimodality of passage time densities in birth-death processes. Statist. Neerlandica 25, 49–55.Google Scholar
18. Keilson, J. and Nunn, W. R. (1979) Laguerre transform as a tool for numerical solution of integral equation of convolution type. Appl. Math. Comput. 5, 313–359.Google Scholar
19. Keilson, J., Nunn, W. R. and Sumita, U. (1981) The bilateral Laguerre transform. Appl. Math. Comput. 8, 137–174.Google Scholar
20. Kingman, J. F. C. (1966) On the algebra of queues. J. Appl. Prob. 3, 285–326.Google Scholar
21. Lukacs, E. and Szász, O. (1951) Certain Fourier transforms of distributions. Canad. J. Math. 3, 140–144.CrossRefGoogle Scholar
22. Lukacs, E. and Szász, O. (1952) Analytic characteristic functions. Pacific. J. Math. 2, 615–625.Google Scholar
23. Lukacs, E. and Szász, O. (1952) Some nonnegative trigonometric polynomials connected with a problem in probability. J. Res. Nat. Bur. Standards, 48, 139–146.Google Scholar
24. Lukacs, E. and Szász, O. (1954) Nonnegative trigonometric polynomials and certain rational characteristic functions. J. Res. Nat. Bur. Standards 52, 153–160.Google Scholar
25. Miller, H. D. (1967) A note on passage times and infinitely divisible distributions. J. Appl. Prob. 4, 402–405.Google Scholar
26. Rosenlund, S. I. (1977) Upwards passage times in the non-negative birth-death processes. Scand. J. Statist. 4, 90–92.Google Scholar
27. Rösler, U. (1980) Unimodality of passage time density for one-dimensional strong Markov processes. Ann. Prob. 8, 853–859.Google Scholar
28. Steutel, F. W. (1967) Note on the infinite divisibility of exponential mixtures. Ann. Math. Statist. 38, 1303–1305.CrossRefGoogle Scholar
29. Steutel, F. W. (1970) Preservation of Infinite Divisibility under Mixing, and Related Topics. Math. Centrum, Amsterdam.Google Scholar
30. Sumita, U. (1981) Development of the Laguerre Transform Method for Numerical Exploration of Applied Probability Models. Ph.D. Dissertation, Graduate School of Management, University of Rochester.Google Scholar
31. Sumita, U. (1984) On the conditional passage time structure of birth-death processes. J. Appl. Prob. 21, 10–21.Google Scholar
32. Sumita, U. (1987) On limiting behavior of ordinary and conditional first passage times for a class of birth-death processes. J. Appl. Prob. 24, 235–240.Google Scholar
33. Szegö, G. (1975) Orthogonal Polynomials, 4th edn. American Mathematical Society Colloquium Publication, Vol. 23.Google Scholar
34. Zemanian, A. H. (1959) On the pole and zero location of rational Laplace transforms of non-negative functions. Proc. Amer. Math. Soc. 10, 868–872.Google Scholar
35. Zemanian, A. H. (1961) On the pole and zero location of rational Laplace transforms of non-negative functions, II. Proc. Amer. Math. Soc. 12, 870–874.CrossRefGoogle Scholar