No CrossRef data available.
Article contents
Bootstrap percolation in random geometric graphs
Published online by Cambridge University Press: 31 May 2023
Abstract
Following Bradonjić and Saniee, we study a model of bootstrap percolation on the Gilbert random geometric graph on the 2-dimensional torus. In this model, the expected number of vertices of the graph is n, and the expected degree of a vertex is 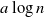 $a\log n$ for some fixed
$a\log n$ for some fixed 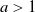 $a>1$. Each vertex is added with probability p to a set
$a>1$. Each vertex is added with probability p to a set 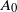 $A_0$ of initially infected vertices. Vertices subsequently become infected if they have at least
$A_0$ of initially infected vertices. Vertices subsequently become infected if they have at least 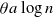 $ \theta a \log n $ infected neighbours. Here
$ \theta a \log n $ infected neighbours. Here 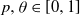 $p, \theta \in [0,1]$ are taken to be fixed constants.
$p, \theta \in [0,1]$ are taken to be fixed constants.
We show that if 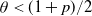 $\theta < (1+p)/2$, then a sufficiently large local outbreak leads with high probability to the infection spreading globally, with all but o(n) vertices eventually becoming infected. On the other hand, for
$\theta < (1+p)/2$, then a sufficiently large local outbreak leads with high probability to the infection spreading globally, with all but o(n) vertices eventually becoming infected. On the other hand, for 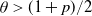 $ \theta > (1+p)/2$, even if one adversarially infects every vertex inside a ball of radius
$ \theta > (1+p)/2$, even if one adversarially infects every vertex inside a ball of radius 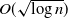 $O(\sqrt{\log n} )$, with high probability the infection will spread to only o(n) vertices beyond those that were initially infected.
$O(\sqrt{\log n} )$, with high probability the infection will spread to only o(n) vertices beyond those that were initially infected.
In addition we give some bounds on the 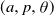 $(a, p, \theta)$ regions ensuring the emergence of large local outbreaks or the existence of islands of vertices that never become infected. We also give a complete picture of the (surprisingly complex) behaviour of the analogous 1-dimensional bootstrap percolation model on the circle. Finally we raise a number of problems, and in particular make a conjecture on an ‘almost no percolation or almost full percolation’ dichotomy which may be of independent interest.
$(a, p, \theta)$ regions ensuring the emergence of large local outbreaks or the existence of islands of vertices that never become infected. We also give a complete picture of the (surprisingly complex) behaviour of the analogous 1-dimensional bootstrap percolation model on the circle. Finally we raise a number of problems, and in particular make a conjecture on an ‘almost no percolation or almost full percolation’ dichotomy which may be of independent interest.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust



