Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Takacs, Lajos
1992.
On the total heights of random rooted trees.
Journal of Applied Probability,
Vol. 29,
Issue. 03,
p.
543.
Bingham, N. H.
1994.
The work of Lajos Takács on probability theory.
Journal of Applied Probability,
Vol. 31,
Issue. A,
p.
29.
Csáki, Endre
1994.
Some joint distributions in Bernoulli excursions.
Journal of Applied Probability,
Vol. 31,
Issue. A,
p.
239.
Csáki, Endre
1996.
On some results for Bernoulli excursions.
Journal of Statistical Planning and Inference,
Vol. 54,
Issue. 1,
p.
45.
Vatutin, V. A.
1996.
On the Maximum of a Simple Random Walk.
Theory of Probability & Its Applications,
Vol. 40,
Issue. 2,
p.
398.
Hazewinkel, M.
1997.
Encyclopaedia of Mathematics.
p.
71.
Aldous, David
1997.
Brownian excursions, critical random graphs and the multiplicative coalescent.
The Annals of Probability,
Vol. 25,
Issue. 2,
Banderier, Cyril
Flajolet, Philippe
Schaeffer, Gilles
and
Soria, Michéle
2000.
Automata, Languages and Programming.
Vol. 1853,
Issue. ,
p.
388.
Kim, Jeong Han
and
Pittel, Boris
2000.
Confirming the Kleitman–Winston Conjecture on the Largest Coefficient in a q-Catalan Number.
Journal of Combinatorial Theory, Series A,
Vol. 92,
Issue. 2,
p.
197.
Martínez, Conrado
and
Molinero, Xavier
2001.
A generic approach for the unranking of labeled combinatorial classes.
Random Structures & Algorithms,
Vol. 19,
Issue. 3-4,
p.
472.
Janson, Svante
2001.
Asymptotic distribution for the cost of linear probing hashing.
Random Structures & Algorithms,
Vol. 19,
Issue. 3-4,
p.
438.
Banderier, Cyril
Flajolet, Philippe
Schaeffer, Gilles
and
Soria, Michèle
2001.
Random maps, coalescing saddles, singularity analysis, and Airy phenomena.
Random Structures & Algorithms,
Vol. 19,
Issue. 3-4,
p.
194.
Fill, James Allen
and
Kapur, Nevin
2004.
Limiting distributions for additive functionals on Catalan trees.
Theoretical Computer Science,
Vol. 326,
Issue. 1-3,
p.
69.
Majumdar, Satya N.
and
Comtet, Alain
2004.
Exact Maximal Height Distribution of Fluctuating Interfaces.
Physical Review Letters,
Vol. 92,
Issue. 22,
Mazza, Christian
2004.
Simply generated trees, B‐series and Wigner processes.
Random Structures & Algorithms,
Vol. 25,
Issue. 3,
p.
293.
Reineke, Markus
2005.
Cohomology of Noncommutative Hilbert Schemes.
Algebras and Representation Theory,
Vol. 8,
Issue. 4,
p.
541.
Majumdar, Satya N.
and
Comtet, Alain
2005.
Airy Distribution Function: From the Area Under a Brownian Excursion to the Maximal Height of Fluctuating Interfaces.
Journal of Statistical Physics,
Vol. 119,
Issue. 3-4,
p.
777.
Majumdar, Satya N.
and
Dasgupta, Chandan
2006.
Spatial survival probability for one-dimensional fluctuating interfaces in the steady state.
Physical Review E,
Vol. 73,
Issue. 1,
Blum, Michael G. B.
François, Olivier
and
Janson, Svante
2006.
The mean, variance and limiting distribution of two statistics sensitive to phylogenetic tree balance.
The Annals of Applied Probability,
Vol. 16,
Issue. 4,
Kearney, Michael J.
2006.
Exactly solvable cellular automaton traffic jam model.
Physical Review E,
Vol. 74,
Issue. 6,


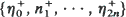 in which
in which 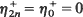 and
and 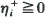 for
for 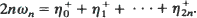 . The results derived have various applications in the theory of probability, including random graphs, tournaments and order statistics.
. The results derived have various applications in the theory of probability, including random graphs, tournaments and order statistics.