Article contents
The behaviour of strategy-frequencies in Parker's model
Published online by Cambridge University Press: 01 July 2016
Extract
Parker's model (or the Scotch Auction) for a contest between two competitors has been studied by Rose (1978). He considers a form of the model in which every pure strategy is playable, and shows that there is no evolutionarily stable strategy (ess). In this paper, in order to discover more about the behaviour of strategies under the model, we shall assume that there are only a finite number of playable pure strategies I1, I2, ···, In where Ij is the strategy ‘play value mj′ and m1 < m2 < ··· < mn. The payoff matrix A for the contest is then given by
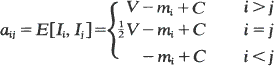 where V is the reward for winning the contest, C is a constant added to ensure that each entry in A is non-negative (see Bishop and Cannings (1978)), and E[Ii, Ij] is the expected payoff for playing Ii against Ij. We also assume that A is regular (Taylor and Jonker (1978)) i.e. that all its rows are independent.
where V is the reward for winning the contest, C is a constant added to ensure that each entry in A is non-negative (see Bishop and Cannings (1978)), and E[Ii, Ij] is the expected payoff for playing Ii against Ij. We also assume that A is regular (Taylor and Jonker (1978)) i.e. that all its rows are independent.
- Type
- Symposium on Mathematical Genetics, London, 26–27 March 1979
- Information
- Copyright
- Copyright © Applied Probability Trust 1980
References
- 2
- Cited by


