Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T07:53:34.631Z Has data issue: false hasContentIssue false
  • English
  • Français

A bang-bang strategy for a finite fuel stochastic control problem

Part of: Stochastic processes Stochastic systems and control

Published online by Cambridge University Press:  01 July 2016

W. D. Sudderth  and
A. P. N. Weerasinghe
W. D. Sudderth*
Affiliation:
University of Minnesota
A. P. N. Weerasinghe*
Affiliation:
Iowa State University
*
∗Postal address: School of Statistics, University of Minnesota, 207 Vincent Hall, 206 Church Street SE, Minneapolis, MN 55455, USA.
∗∗Department of Mathematics, Iowa State University, Ames, IA 50010, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

The problem treated is that of controlling a process 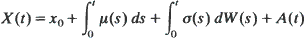with values in [0, a]. The non-anticipative controls (µ(t), σ(t)) are selected from a set C(x) whenever X(t–) = x and the non-decreasing process A(t) is chosen by the controller subject to the condition 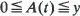where y is a constant representing the initial amount of fuel. The object is to maximize the probability that X(t) reaches a. The optimal process is determined when the function 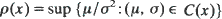has a unique minimum on [0, a] and satisfies certain regularity conditions. The optimal process is a combination of ‘timid play' in which fuel is used gradually in the form of local time at 0, and ‘bold play' in which all the fuel is used at once.

Keywords

GAMBLINGBOLD PLAYTIMID PLAYLOCAL TIME

MSC classification

Primary: 93E20: Optimal stochastic control
Secondary: 60G40: Stopping times; optimal stopping problems; gambling theory
Type
Research Article
Information
Advances in Applied Probability , Volume 24 , Issue 3 , September 1992 , pp. 589 - 603
Copyright
Copyright © Applied Probability Trust 1992 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by National Science Foundation Grants DMS-8801085 and DMS-8911548.

References

[1] Benes, V. E., Shepp, L. A. and Witsenhausen, H. S. (1980) Some solvable stochastic control problems. Stochastics 4, 39–83.Google Scholar
[2] Karatzas, I. and Shreve, S. E. (1986) Equivalent models for finite fuel stochastic control. Stochastics 18, 245–276.Google Scholar
[3] Pestien, V. and Sudderth, W. (1985) Continuous-time red and black: how to control a diffusion to a goal. Math. Operat. Res. 10, 599–611.Google Scholar
[4] Pestien, V. and Sudderth, W. (1988) Continuous-time casino problems. Math. Operat. Res. 13, 364–376.Google Scholar
[5] Protter, M. H. and Weinberger, H. F. (1967) Maximum Principles in Differential Equations . Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
[6] Sudderth, W. D. and Weerasinghe, A. P. N. (1991) Using fuel to control a process to a goal. Stochastics 34, 169–186.Google Scholar