Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T07:42:42.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximations for the repairman problem with two repair facilities, II: Spares

Published online by Cambridge University Press:  01 July 2016

Donald L. Iglehart  and
Austin J. Lemoine
Donald L. Iglehart
Affiliation:
Stanford University
Austin J. Lemoine
Affiliation:
Control Analysis Corporation
Get access Rights & Permissions [Opens in a new window]

Abstract

The model considered here consists of n operating units which are subject to stochastic failure according to an exponential failure time distribution. These operating units are backed up by mn spare units. Failures can be of two types. With probability p (q) a failure is of type 1(2) and is sent to repair facility 1(2) for repair. Repair facility 1(2) operates as a 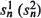-server queue with exponential repair times having parameter μ1 (μ2). The number of units waiting for or undergoing repair at each of the two facilities is a continuous parameter Markov chain with finite state space. This paper derives limit theorems for the stationary distribution of this Markov chain as n becomes large under the assumption that 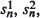and mn grow linearly with n. These limit theorems give very useful approximations, in terms of the seven parameters characterizing the model, to a distribution that would be difficult to calculate in practice.

Keywords

BIRTH AND DEATH PROCESSESCENTRAL LIMIT THEOREMLOCAL CENTRAL LIMIT THEOREMSLOGISTICS SYSTEMSREPAIRMAN PROBLEMREVERSIBLE MARKOV CHAINSWEAK LAW OF LARGE NUMBERS
Type
Research Article
Information
Advances in Applied Probability , Volume 6 , Issue 1 , March 1974 , pp. 147 - 158
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Heathcote, C. (1967) Complete exponential convergence. J. Appl. Prob. 4, 217–256.Google Scholar
[2] Iglehart, D. L. (1964) Reversible competition processes. Z. Wahrscheinlichkeitsth. 2, 314–331.Google Scholar
[3] Iglehart, D. L. and Lemoine, A. (1973) Approximations for the repairman problem with two repair facilities, I: no spares. Adv. Appl. Prob. 5, 595–613.Google Scholar