Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-12T11:12:42.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation of the invariant measure for stable stochastic differential equations by the Euler–Maruyama scheme with decreasing step sizes

Part of: Stochastic processes Approximation methods and numerical treatment of dynamical systems Stochastic analysis

Published online by Cambridge University Press:  31 March 2025

Peng Chen ,
Xinghu Jin ,
Yimin Xiao  and
Lihu Xu
Peng Chen*
Affiliation:
Nanjing University of Aeronautics and Astronautics
Xinghu Jin*
Affiliation:
Hefei University of Technology
Yimin Xiao*
Affiliation:
Michigan State University
Lihu Xu*
Affiliation:
University of Macau and Zhuhai UM Science and Technology Research Institute
*
*Postal address: School of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing, 211106, China. Email: [email protected]
**Postal address: School of Mathematics, Hefei University of Technology, Hefei, Anhui, 230601, China. Email: [email protected]
***Postal address: Department of Statistics and Probability, Michigan State University, 619 Red Cedar Road East Lansing, MI 48824, USA. Email: [email protected]
****Postal address: Department of Mathematics, Faculty of Science and Technology, University of Macau, Macau S.A.R., China. Zhuhai UM Science and Technology Research Institute, Zhuhai, China. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 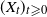$(X_t)_{t \geqslant 0}$ be the solution of the stochastic differential equation

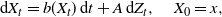\[\mathrm{d} X_t = b(X_t) \,\mathrm{d} t+A\,\mathrm{d} Z_t, \quad X_{0}=x,\]
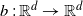where $b\,:\, \mathbb{R}^d \rightarrow \mathbb{R}^d$ is a Lipschitz-continuous function, 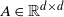$A \in \mathbb{R}^{d \times d}$ is a positive-definite matrix, 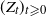$(Z_t)_{t\geqslant 0}$ is a d-dimensional rotationally symmetric $\alpha$-stable Lévy process with 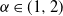$\alpha \in (1,2)$ and 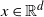$x\in\mathbb{R}^{d}$. We use two Euler–Maruyama schemes with decreasing step sizes 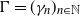$\Gamma = (\gamma_n)_{n\in \mathbb{N}}$ to approximate the invariant measure of 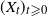$(X_t)_{t \geqslant 0}$: one uses independent and identically distributed $\alpha$-stable random variables as innovations, and the other employs independent and identically distributed Pareto random variables. We study the convergence rates of these two approximation schemes in the Wasserstein-1 distance. For the first scheme, under the assumption that the function b is Lipschitz and satisfies a certain dissipation condition, we demonstrate a convergence rate of 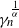$\gamma^{\frac{1}{\alpha}}_n$. This convergence rate can be improved to 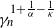$\gamma^{1+\frac {1}{\alpha}-\frac{1}{\kappa}}_n$ for any 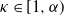$\kappa \in [1,\alpha)$, provided b has the additional regularity of bounded second-order directional derivatives. For the second scheme, where the function b is assumed to be twice continuously differentiable, we establish a convergence rate of 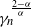$\gamma^{\frac{2-\alpha}{\alpha}}_n$; moreover, we show that this rate is optimal for the one-dimensional stable Ornstein–Uhlenbeck process. Our theorems indicate that the recent significant result of [34] concerning the unadjusted Langevin algorithm with additive innovations can be extended to stochastic differential equations driven by an $\alpha$-stable Lévy process and that the corresponding convergence rate exhibits similar behaviour. Compared with the result in [6], our assumptions have relaxed the second-order differentiability condition, requiring only a Lipschitz condition for the first scheme, which broadens the applicability of our approach.

Keywords

Euler–Maruyama schemedecreasing step sizeWasserstein-1 distance

MSC classification

Primary: 60H10: Stochastic ordinary differential equations 37M25: Computational methods for ergodic theory (approximation of invariant measures, computation of Lyapunov exponents, entropy) 60G51: Processes with independent increments; L'evy processes
Secondary: 60H07: Stochastic calculus of variations and the Malliavin calculus 60H35: Computational methods for stochastic equations 60G52: Stable processes
Type
Original Article
Information
Advances in Applied Probability , First View , pp. 1 - 31
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Angeli, L., Crisan, D. and Ottobre, M. (2023). Uniform in time convergence of numerical schemes for stochastic differential equations via strong exponential stability: Euler methods, split-step and tamed schemes. Preprint. Available at https://arxiv.org/abs/2303.15463.Google Scholar
Arras, B. and Houdré, C. (2019). On Stein’s method for multivariate self-decomposable laws. Electronic Journal of Probability. 24, 1–63.Google Scholar
Bally, V. and Talay, D. (1996). The law of the Euler scheme for stochastic differential equations. Probability Theory and Related Fields. 104, 43–60.CrossRefGoogle Scholar
Bao, J. H., Huang, X. and Yuan, C. G. (2019). Convergence rate of Euler–Maruyama scheme for SDEs with Hölder-Dini continuous drifts. Journal of Theoretical Probability. 32(2), 848–871.CrossRefGoogle Scholar
Butkovsky, O., Dareiotis, K. and Gerencsér, M. (2022). Strong rate of convergence of the Euler scheme for SDEs with irregular drift driven by Lévy noise. arXiv preprint https://arxiv.org/abs/arXiv:2204.12926.Google Scholar
Chen, P., Deng, C. S., Schilling, R. and Xu, L. H. (2023). Approximation of the invariant measure of stable SDEs by an Euler–Maruyama scheme. Stochastic Processes and their Applications. 163, 136–167.Google Scholar
Chen, P., Nourdin, I., Xu, L. H. and Yang, X. C. (2023). Multivariate stable approximation by Stein’s method. Journal of Theoretical Probability. 37(1), 446–488.CrossRefGoogle Scholar
Chen, P. and Xu, L. H. (2019). Approximation to stable law by the Lindeberg principle. Journal of Mathematical Analysis and Applications. 480(2), 123338.Google Scholar
Chambers, J., Mallows, C. and Stuck, B. (1976). A method for simulating stable random variables. Journal of the American Statistical Association. 71, 340–344.CrossRefGoogle Scholar
Dalalyan, A. S. (2017). Theoretical guarantees for approximate sampling from smooth and log-concave densities. Journal of the Royal Statistical Society. Series B (Statistical Methodology). 79, 651–676.Google Scholar
Da Prato, G. and Zabczyk, J. (2003). Ergodicity for Infinite Dimensional Systems. Cambridge University Press.Google Scholar
Dareiotis, K. and Gerencs, M. (2020). On the regularisation of the noise for the Euler–Maruyama scheme with irregular drift. Electronic Journal of Probability. 25, 1–18.Google Scholar
Durmus, A. and Moulines, E. (2017). Nonasymptotic convergence analysis for the unadjusted Langevin algorithm. The Annals of Applied Probability. 27(3), 1551–1587.CrossRefGoogle Scholar
Durmus, A. and Moulines, E. (2019). High-dimensional Bayesian inference via the unadjusted Langevin algorithm. Bernoulli. 25(4A), 2854–2882.CrossRefGoogle Scholar
Fang, X., Shao, Q. M., Xu, L. H. (2019). Multivariate approximations in Wasserstein distance by Stein’s method and Bismut’s formula. Probability Theory and Related Fields. 174(3), 945–979.Google Scholar
Hairer, M. (2010). Convergence of Markov processes. Lecture notes, 18, 26.Google Scholar
Hashimoto, H. (2013). Approximation and stability of solutions of SDEs driven by a symmetric $\alpha$ -stable process with non-Lipschitz coefficients. Séminaire de probabilités XLV. 181–199.Google Scholar
Huang, X. and Liao, Z. W. (2018). The Euler–Maruyama method for S(F)DEs with Hölder drift and $\alpha$ -stable noise. Stochastic Analysis and Applications. 36(1), 28–39.Google Scholar
Jacod, J. (2004). The Euler scheme for Lévy driven stochastic differential equations: limit theorems. The Annals of Probability. 32, 1830–1872.Google Scholar
Janicki, A., Michna, Z. and Weron, A. (1996). Approximation of stochastic differential equations driven by $\alpha$ -stable Lévy motion. Applicationes Mathematicae. 24, 149–168.CrossRefGoogle Scholar
Kühn, F. and Schilling, R. L. (2019). Strong convergence of the Euler–Maruyama approximation for a class of Lévy-driven SDEs. Stochastic Processes and their Applications. 129(8), 2654–2680.CrossRefGoogle Scholar
Li, X., Wang, F. Y. and Xu, L. H. (2023). Unadjusted Langevin algorithms for SDEs with Hölder drift. arxiv preprint https://arxiv.org/abs/arxiv:2310.00232.Google Scholar
Li, Y. and Zhao, G. (2023). Euler–Maruyama scheme for SDE driven by Lévy process with Hölder drift. arXiv preprint https://arxiv.org/abs/arXiv:2304.13952.Google Scholar
Li, Y., Mao, X. R., Song, Q., Wu, F. K. and Yin, G. (2023). Strong convergence of Euler–Maruyama schemes for McKean-Vlasov stochastic differential equations under local Lipschitz conditions of state variables. IMA Journal of Numerical Analysis. 43(2), 1001–1035.Google Scholar
Li, X., Ma, Q., Yang, H. and Yuan, C. G. (2018). The numerical invariant measure of stochastic differential equations with Markovian switching. SIAM Journal on Numerical Analysis. 56, 1435–1455.CrossRefGoogle Scholar
Liang, M, Schilling, R. L. and Wang, J. (2020). A unified approach to coupling SDEs driven by Lévy noise and some applications. Bernoulli. 26(1), 664–693.CrossRefGoogle Scholar
Liang, M. and Wang, J. (2020). Gradient estimates and ergodicity for SDEs driven by multiplicative Lévy noises via coupling. Stochastic Processes and their Applications. 130(5), 3053–3094.CrossRefGoogle Scholar
Lim, S. H., Wan. Y. and Simsekli, U. (2022). Chaotic regularization and heavy-tailed limits for deterministic gradient descent. Advances in Neural Information Processing Systems. 35, 26590–26602.Google Scholar
Marion, G., Mao, X. R., Renshaw, E. (2002). Convergence of the Euler scheme for a class of stochastic differential equations. International Mathematical Journal. 1(1), 9–22.Google Scholar
Mimica, A., Sandrić, N. and Schilling, R. L. (2018). Markov chain approximation of pure jump processes. Acta Applicandae Mathematicae. 158, 167–206.CrossRefGoogle Scholar
Neu, G., Dziugaite, G. K., Haghifam, M. and Roy, D. M. (2021). Information-theoretic generalization bounds for stochastic gradient descent. Conference on Learning Theory. 3526–3545.Google Scholar
Nguyen, T. H., Simsekli, U., Gurbuzbalaban, M. and Richard, G. (2019). First exit time analysis of stochastic gradient descent under heavy-tailed gradient noise. Advances in Neural Information Processing Systems. 32, 273–283.Google Scholar
Nolan, J. P. (2020). Univariate stable distributions: models for heavy tailed data. Springer, Berlin. 101-130.Google Scholar
Pagès, G. and Panloup, F. (2023). Unadjusted Langevin algorithm with multiplicative noise: Total variation and Wasserstein bounds. The Annals of Applied Probability. 33(1), 726–779.CrossRefGoogle Scholar
Pamen, O. M. and Taguchi, D. (2017). Strong rate of convergence for the Euler–Maruyama approximation of SDEs with Hölder continuous drift coefficient. Stochastic Processes and their Applications. 127(8), 2542–2559.Google Scholar
Panloup, F. (2008). Recursive computation of the invariant measure of a stochastic differential equation driven by a Lévy process. The Annals of Applied Probability. 18(2), 379–426.Google Scholar
Protter, P. and Talay, D. (1997). The Euler scheme for Lévy driven stochastic differential equations. The Annals of Probability. 25(1), 393–423.CrossRefGoogle Scholar
Raj, A., Barsbey, M., Gurbuzbalaban, M., Zhu, L. and Simsekli, U. (2023). Algorithmic stability of heavy-tailed SGD with general loss functions, Proceedings of the 40th International Conference on Machine Learning, Honolulu, Hawaii, USA. PMLR 202.Google Scholar
Raj, A., Barsbey, M., Gürbüzbalaban, M., Zhu, L. and Simsekli, U. (2022). Algorithmic stability of heavy-tailed stochastic gradient descent on least squares. arXiv preprint https://arxiv.org/abs/arXiv:2206.01274.Google Scholar
Samorodnitsky, G. and Taqqu, M. S. Stable non-Gaussian random processes. Stochastic Modeling. Chapman & Hall, New York, 1994.Google Scholar
Sanz-Serna, J. M. and Zygalakis, K. C. (2021). Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations. Journal of Machine Learning Research. 22, 1–37.Google Scholar
Shao, J. (2018). Invariant measures and Euler–Maruyama’s approximations of state-dependent regime-switching diffusions. SIAM Journal on Control and Optimization. 56(5), 3215–3238.Google Scholar
Villani, C. (2009). Optimal transport: old and new. (Vol. 338, p. 23). Berlin: Springer.Google Scholar
Tarami, B. and Avaji, M. (2018). Convergence of Euler–Maruyama method for stochastic differential equations driven by $\alpha$ -stable Lévy motion. Journal of Mathematical Extension. 12, 31–53.Google Scholar
Wang, F. Y., Xu, L. H. and Zhang, X. C. (2015). Gradient estimates for SDEs driven by multiplicative Lévy noise. Journal of Functional Analysis. 269(10), 3195–3219.CrossRefGoogle Scholar
Wang, J. (2016). $L^p$ -Wasserstein distance for stochastic differential equations driven by Lévy processes. Bernoulli. 22(3), 1598–1616.Google Scholar
Yuan, C. G. and Mao, X. R. (2008). A note on the rate of convergence of the Euler–Maruyama method for stochastic differential equations. Stochastic Analysis and Applications. 26(2), 325–333.CrossRefGoogle Scholar
Zhang, X. C. (2013). Derivative formulas and gradient estimates for SDEs driven by $\alpha$ -stable processes. Stochastic Processes and their Applications. 123(4), 1213–1228.Google Scholar