Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-20T16:22:41.529Z Has data issue: false hasContentIssue false
  • English
  • Français

An ordering inequality for exchangeable random variables

Published online by Cambridge University Press:  01 July 2016

G. S. Watson
G. S. Watson*
Affiliation:
Princeton University
*
∗Postal address: Department of Statistics, Princeton University, Fine Hall, Washington Road, Princeton, NJ 08544, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X1, · ··, Xn be exchangeable random variables with finite variance and two sequences of constants satisfying a1≦···≦an, b1≦···≦bn. Suppose that a′1, ···, a′n is a rearrangement of a1, ···, an and that g(x) is a non-decreasing function. Then

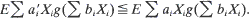
Type
Letters to the Editor
Information
Advances in Applied Probability , Volume 18 , Issue 1 , March 1986 , pp. 274 - 276
Copyright
Copyright © Applied Probability Trust 1986 

Footnotes

The writing of this paper was partially supported by Grant DMS 842–1301 from the National Science Foundation to the Department of Statistics, Princeton University.

References

Hardy, G. H., Littlewood, J. E., and Polya, G. (1934) Inequalities. Cambridge University Press.Google Scholar
Watson, G. S. (1985) Some theory of estimation on the sphere. Ann. Inst. Statist. Math. To appear.Google Scholar