Article contents
 $\alpha$-Stable convergence of heavy-/light-tailed infinitely wide neural networks
$\alpha$-Stable convergence of heavy-/light-tailed infinitely wide neural networks
Published online by Cambridge University Press: 03 July 2023
Abstract
We consider infinitely wide multi-layer perceptrons (MLPs) which are limits of standard deep feed-forward neural networks. We assume that, for each layer, the weights of an MLP are initialized with independent and identically distributed (i.i.d.) samples from either a light-tailed (finite-variance) or a heavy-tailed distribution in the domain of attraction of a symmetric  $\alpha$-stable distribution, where
$\alpha$-stable distribution, where 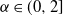 $\alpha\in(0,2]$ may depend on the layer. For the bias terms of the layer, we assume i.i.d. initializations with a symmetric
$\alpha\in(0,2]$ may depend on the layer. For the bias terms of the layer, we assume i.i.d. initializations with a symmetric  $\alpha$-stable distribution having the same
$\alpha$-stable distribution having the same  $\alpha$ parameter as that layer. Non-stable heavy-tailed weight distributions are important since they have been empirically seen to emerge in trained deep neural nets such as the ResNet and VGG series, and proven to naturally arise via stochastic gradient descent. The introduction of heavy-tailed weights broadens the class of priors in Bayesian neural networks. In this work we extend a recent result of Favaro, Fortini, and Peluchetti (2020) to show that the vector of pre-activation values at all nodes of a given hidden layer converges in the limit, under a suitable scaling, to a vector of i.i.d. random variables with symmetric
$\alpha$ parameter as that layer. Non-stable heavy-tailed weight distributions are important since they have been empirically seen to emerge in trained deep neural nets such as the ResNet and VGG series, and proven to naturally arise via stochastic gradient descent. The introduction of heavy-tailed weights broadens the class of priors in Bayesian neural networks. In this work we extend a recent result of Favaro, Fortini, and Peluchetti (2020) to show that the vector of pre-activation values at all nodes of a given hidden layer converges in the limit, under a suitable scaling, to a vector of i.i.d. random variables with symmetric  $\alpha$-stable distributions,
$\alpha$-stable distributions, 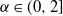 $\alpha\in(0,2]$.
$\alpha\in(0,2]$.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 4
- Cited by



