Article contents
Yaglom limit for stochastic fluid models
Published online by Cambridge University Press: 08 October 2021
Abstract
In this paper we analyse the limiting conditional distribution (Yaglom limit) for stochastic fluid models (SFMs), a key class of models in the theory of matrix-analytic methods. So far, only transient and stationary analyses of SFMs have been considered in the literature. The limiting conditional distribution gives useful insights into what happens when the process has been evolving for a long time, given that its busy period has not ended yet. We derive expressions for the Yaglom limit in terms of the singularity˜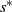 $s^*$ such that the key matrix of the SFM,
$s^*$ such that the key matrix of the SFM, 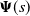 ${\boldsymbol{\Psi}}(s)$, is finite (exists) for all
${\boldsymbol{\Psi}}(s)$, is finite (exists) for all 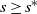 $s\geq s^*$ and infinite for
$s\geq s^*$ and infinite for 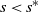 $s<s^*$. We show the uniqueness of the Yaglom limit and illustrate the application of the theory with simple examples.
$s<s^*$. We show the uniqueness of the Yaglom limit and illustrate the application of the theory with simple examples.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s) 2021. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by



