Synchronous service on a circle

Abstract

In this paper, we study a synchronous computer network model which may be described as follows. There are n service stations around a circle and there are k people to be serviced 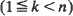with at most one person per station. Time is slotted and in each time slot b adjacent people with an empty station ahead can move synchronously and simultaneously to the next counterclockwise station with probability p^b. We show that the stationary distribution is uniform on all 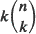possible states, and using the Descartes' rule of signs we find the optimal value of k (fixed p and n) that yields maximal ‘throughput', i.e., the expected number of people served per time slot in equilibrium. We also briefly study an asynchronous model (introduced by D. Sarkar) where in each time slot a person moves with probability p to the next counterclockwise station if it is empty. We find, among other results, the new stationary distribution (Ramakrishnan et al. (1989) also find independently the stationary distribution and they also find the optimal value of k (fixed p and n) that yields maximal throughput in this model). We give tables comparing the synchronous and asynchronous models. Some applications which motivate this study are briefly presented.