Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fendick, K.W.
and
Whitt, W.
1989.
Measurements and approximations to describe the offered traffic and predict the average workload in a single-server queue.
Proceedings of the IEEE,
Vol. 77,
Issue. 1,
p.
171.
Kella, Offer
and
Whitt, Ward
1990.
Diffusion approximations for queues with server vacations.
Advances in Applied Probability,
Vol. 22,
Issue. 3,
p.
706.
Gallot, S. F. L.
1993.
Absorption and first-passage times for a compound Poisson process in a general upper boundary.
Journal of Applied Probability,
Vol. 30,
Issue. 4,
p.
835.
Harrison, J. Michael
1998.
Heavy traffic analysis of a system with parallel servers: asymptotic optimality of discrete-review policies.
The Annals of Applied Probability,
Vol. 8,
Issue. 3,
Asmussen, Søren
and
Kella, Offer
2001.
On optional stopping of some exponential martingales for Lévy processes with or without reflection.
Stochastic Processes and their Applications,
Vol. 91,
Issue. 1,
p.
47.
Konstantopoulos, Takis
and
Richardson, Gregory S.
2002.
Conditional limit theorems for spectrally positive Lévy processes.
Advances in Applied Probability,
Vol. 34,
Issue. 1,
p.
158.
Kella, Offer
2007.
Encyclopedia of Statistics in Quality and Reliability.
2008.
Stochastic Processes for Insurance & Finance.
p.
617.
Lewis, Alan L.
and
Mordecki, Ernesto
2008.
Wiener-Hopf Factorization for Lévy Processes Having Positive Jumps with Rational Transforms.
Journal of Applied Probability,
Vol. 45,
Issue. 1,
p.
118.
Czystołowski, M.
and
Szczotka, W.
2010.
Queueing approximation of suprema of spectrally positive Lévy process.
Queueing Systems,
Vol. 64,
Issue. 4,
p.
305.
Kella, Offer
2012.
The Class of Distributions Associated with the Generalized Pollaczek-Khinchine Formula.
Journal of Applied Probability,
Vol. 49,
Issue. 3,
p.
883.
M. Asghari, Naser
Iseger, Peter
and
Mandjes, Michael
2012.
Numerical Techniques in Lévy Fluctuation Theory.
Methodology and Computing in Applied Probability,
Kella, Offer
2012.
The Class of Distributions Associated with the Generalized Pollaczek-Khinchine Formula.
Journal of Applied Probability,
Vol. 49,
Issue. 03,
p.
883.
Kella, Offer
2014.
Wiley StatsRef: Statistics Reference Online.
Michna, Zbigniew
Palmowski, Zbigniew
and
Pistorius, Martijn
2015.
The distribution of the supremum for spectrally asymmetric Lévy
processes.
Electronic Communications in Probability,
Vol. 20,
Issue. none,
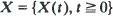 be a process with stationary, independent increments and no negative jumps. Let
be a process with stationary, independent increments and no negative jumps. Let 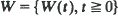 be this same process modified by a reflecting barrier at zero (a storage process). Assuming that –
be this same process modified by a reflecting barrier at zero (a storage process). Assuming that – 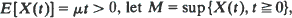 and denote by ψ(s) the exponent function of X. A simple formula is derived for the Laplace transform of
and denote by ψ(s) the exponent function of X. A simple formula is derived for the Laplace transform of 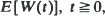 as a function of W(0). Using the fact that the distribution of M is the unique stationary distribution of the Markov process W, this yields an elementary proof that the Laplace transform of M is µs/ψ(s). If
as a function of W(0). Using the fact that the distribution of M is the unique stationary distribution of the Markov process W, this yields an elementary proof that the Laplace transform of M is µs/ψ(s). If 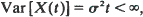 it follows that
it follows that 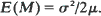 These surprisingly simple formulas were originally obtained by Zolotarev using analytical methods.
These surprisingly simple formulas were originally obtained by Zolotarev using analytical methods.

