Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T07:44:56.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic Discounting, Aggregate Claims, and the Bootstrap

Part of: Applications

Published online by Cambridge University Press:  01 July 2016

M. Aebi ,
P. Embrechts  and
T. Mikosch
M. Aebi*
Affiliation:
ETH-Zürich
P. Embrechts*
Affiliation:
ETH-Zürich
T. Mikosch*
Affiliation:
Victoria University of Wellington
*
* Postal address: Department of Mathematics, ETH-Zürich, CH-8092 Zürich, Switzerland.
* Postal address: Department of Mathematics, ETH-Zürich, CH-8092 Zürich, Switzerland.
** Postal address: Institute of Statistics and Operations Research, Victoria University, P.O. Box 600, Wellington, New Zealand.
Get access Rights & Permissions [Opens in a new window]

Abstract

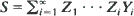Obtaining good estimates for the distribution function of random variables like (‘perpetuity’) and 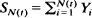(‘aggregate claim amount’), where the (Yi), (Zi) are independent i.i.d. sequences and (N(t)) is a general point process, is a key question in insurance mathematics. In this paper, we show how suitably chosen metrics provide a theoretical justification for bootstrap estimation in these cases. In the perpetuity case, we also give a detailed discussion of how the method works in practice.

Keywords

BOOTSTRAPPERPETUITYPROBABILITY METRICSRISK THEORYSTOCHASTIC DISCOUNTING

MSC classification

Primary: 62P05: Applications to actuarial sciences and financial mathematics
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 26 , Issue 1 , March 1994 , pp. 183 - 206
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bickel, F. and Freedman, D. A. (1981) Some asymptotic theory for the bootstrap. Ann. Statist. 9, 1196–1217.Google Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1988) Regular Variation. Cambridge University Press.Google Scholar
Brandt, A., Franken, P. and Lisek, B. (1990) Stationary Stochastic Models. Wiley, New York.Google Scholar
Chow, Y. S. and Teicher, H. (1978) Probability Theory. Independence, Interchangeability, Martingales. Springer-Verlag, New York.Google Scholar
Csörgö, M. and Horvath, L. (1988) On the distributions of Lp norms of weighted uniform empirical and quantile processes. Ann. Prob. 16, 142–161.Google Scholar
Dehling, H. and Mikosch, T. (1992) Random quadratic forms and the bootstrap for U-statistics. J. Multivariate Anal. To appear.Google Scholar
Delbaen, F. and Haezendonck, J. M. (1987) Classical risk theory in an economic environment. Insurance: Math. Econ. 6, 85–116.Google Scholar
Dudley, R. M. (1976) On the speed of mean Glivenko-Cantelli convergence. Ann. Math. Statist. 40, 40–50.Google Scholar
Dufresne, D. (1990) The distribution of a perpetuity, with applications to risk theory and pension funding. Scand. Actuarial J. No. 1-2, 39–79.Google Scholar
Dufresne, D. (1992) On discounting when rates of return are random. Trans. 24th Internat. Congr. Actuaries, Montréal.Google Scholar
Embrechts, P. and Mikosch, T. (1991) A bootstrap procedure for estimating the adjustment coefficient. Insurance: Math. Econ. 10, 181–190.Google Scholar
Feilmeier, M. and Bertram, J. (1987) Anwendungen numerischer Methoden in der Risikotheorie. DGVM, Heft 16, Verlag Versicherungswirtschaft e.V., Karlsruhe.Google Scholar
Gine, E. (1992) Emprical processes and applications. Principal lecture. Abstr. 20th European Meeting of Statisticians, Bath, 52–53.Google Scholar
Gine, E. and Zinn, J. (1990) Bootstrapping general empirical measures. Ann. Prob. 10, 851–869.Google Scholar
Goldie, C. M. (1991) Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Prob. 1, 126–166.Google Scholar
Gut, A. (1988) Stopped Random Walks. Limit Theorems and Applications. Springer-Verlag, New York.CrossRefGoogle Scholar
Kalashnikov, V. V. and Rachev, S. T. (1990) Mathematical Methods for Construction of Queueuing Models. Wadsworth, Pacific Grove.Google Scholar
Pitts, S. (1992) Nonparametric estimation of compound distributions with applications in insurance. Research Report 111, University College London.Google Scholar
Rachev, S. T. (1984) The Monge-Kontorovich mass transference problem and its stochastic applications. Theory Prob. Appl. 29, 647–676.Google Scholar
Rachev, S. T. (1991) Probability Metrics and the Stability of Stochastic Models. Wiley, New York.Google Scholar
Rachev, S. T. and Rüschendorf, L. (1991) Probability metrics and recursive algorithms. Preprint.Google Scholar
Rachev, S. T. and Rüschendorf, L. (1992) Rate of convergence for sums and maxima and doubly ideal metrics. Theory Prob. Appl. 37, 276–290.Google Scholar
Rachev, S. T. and Samorodnitsky, G. (1991) Limit laws for a stochastic process and random recursion arising in probabilistic modelling. Preprint.Google Scholar
Rachev, S. T. and Todorovic, P. (1990) On the rate of convergence of some functionals of a stochastic process. J. Appl. Prob. 27, 805–814.Google Scholar
Serfling, R. J. (1980) Approximation Theorems of Mathematical Statistics. Wiley, New York.Google Scholar
Todorovic, P. and Gani, J. (1987) Modelling the effect of erosion on crop production. J. Appl. Prob. 24, 787–797.Google Scholar
Vervaat, W. (1979) On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.CrossRefGoogle Scholar
Von Bahr, B. and Esseen, C. G. (1965) Inequalities for the rth absolute moment of a sum of random variables. Ann. Math. Statist. 36, 299–303.CrossRefGoogle Scholar
Wellner, J. A. (1992) Empirical processes in action: a review. Internat. Statist. Rev. 60, 247–270.Google Scholar
Zolotarev, V. M. (1976) Metric distances in spaces of random variables and their distributions. Math. USSR Sb. 30, 373–401.Google Scholar
Zolotarev, V. M. (1986) Contemporary Theory of Summation of Independent Random Variables. Nauka, Moscow (in Russian).Google Scholar