Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T06:10:54.226Z Has data issue: false hasContentIssue false
  • English
  • Français

On the multiserver queue with finite waiting room and controlled input

Published online by Cambridge University Press:  01 July 2016

Jewgeni Dshalalow
Jewgeni Dshalalow*
Affiliation:
Technische Universität, Berlin
*
∗Postal address: Technische Universitat Berlin, FB Mathematik, Sekretariat MA 7-5, Strasse des 17. Juni, 1000 Berlin 12, West Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study a multi-channel queueing model of type 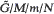with N waiting places and a non-recurrent input flow dependent on queue length at the time of each arrival. The queue length is treated as a basic process. We first determine explicitly the limit distribution of the embedded Markov chain. Then, by introducing an auxiliary Markov process, we find a simple relationship between the limiting distribution of the Markov chain and the limiting distribution of the original process with continuous time parameter. Here we simultaneously combine two methods: solving the corresponding Kolmogorov system of the differential equations, and using an approach based on the theory of semi-regenerative processes. Among various applications of multi-channel queues with state-dependent input stream, we consider a closed single-server system with reserve replacement and state-dependent service, which turns out to be dual (in a certain sense) in relation to our model; an optimization problem is also solved, and an interpretation by means of tandem systems is discussed.

Keywords

QUEUE LENGTHASYMPTOTIC DISTRIBUTIONSEMI-REGENERATIVE PROCESSCLOSED QUEUETANDEM QUEUE
Type
Research Article
Information
Advances in Applied Probability , Volume 17 , Issue 2 , June 1985 , pp. 408 - 423
Copyright
Copyright © Applied Probability Trust 1985 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This paper is based on part of a doctoral dissertation submitted to the Department of Mathematics, Technical University of Berlin.

References

Abol’Nikov, L. M. and Dzhalalov, J. A. (1978) Feedback queueing systems; duality principle and optimization. Automation and Remote Control 39 (1), 11–20.Google Scholar
Çinlar, E. (1975) Introduction to Stochastic Processes. Prentice Hall, Englewood Cliffs, NJ.Google Scholar
Dzhalalov, J. A. (1978) Many-server feedback queueing systems. Engineering Cybernetics 16 (3), 78–88.Google Scholar
Dshalalov, J. A. (1983) Warteschlangensysteme mit Feedback. Doctoral Dissertation, Technische Universität, Berlin.Google Scholar
Schäl, ?. (1971) The analysis of queues with state-dependent parameters by Markov renewal processes. Adv. Appl. Prob. 3, 155–175.CrossRefGoogle Scholar
Takács, L. (1958) Some probability questions in the theory of telephone traffic (in Hungarian). Mag. Tud. Acad. Mat. Fiz. Oszl. Közl. 8, 151–210.Google Scholar
Takács, L. (1962) Introduction to the Theory of Queues. Oxford University Press, New York.Google Scholar