Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T02:56:19.604Z Has data issue: false hasContentIssue false
  • English
  • Français

On the asymptotic behaviour of branching processes with infinite mean

Published online by Cambridge University Press:  01 July 2016

H.-J. Schuh  and
A. D. Barbour
H.-J. Schuh
Affiliation:
Division of Mathematics and Statistics, C.S.I.R.O., Canberra
A. D. Barbour
Affiliation:
University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper deals with the asymptotic behaviour of infinite mean Galton–Watson processes (denoted by {Zn}). We show that these processes can be classified as regular or irregular. The regular ones are characterized by the property that for any sequence of positive constants {Cn}, for which 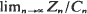a.s. exists, 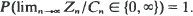The irregular ones, which will be shown by examples to exist, have the property that there exists a sequence of constants {Cn} such that 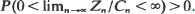In Part 1 we study the properties of {Zn/Cn} and give some characterizations for both regular and irregular processes. Part 2 starts with an a.s. convergence result for {yn(Zn)}, where {yn} is a suitable chosen sequence of functions related to {Zn}. Using this, we then derive necessary and sufficient conditions for the a.s. convergence of {U(Zn)/Cn}, where U is a slowly varying function. The distribution function of the limit is shown to satisfy a Poincaré functional equation. Finally we show that for every process {Zn} it is possible to construct explicitly functions U, such that U(Zn)/en converges a.s. to a non-degenerate proper random variable. If the process is regular, all these functions U are slowly varying. The distribution of the limit depends on U, and we show that by appropriate choice of U we may get a limit distribution which has a positive and continuous density or is continuous but not absolutely continuous or even has no probability mass on certain intervals. This situation contrasts strongly with the finite mean case.

Keywords

GALTON-WATSON PROCESS WITH INFINITE MEANALMOST SURE CONVERGENCEMARTINGALESNON-DEGENERATE AND PROPER RANDOM VARIABLECUMULANT GENERATING FUNCTIONREGULAR AND IRREGULAR POINTSREGULAR AND IRREGULAR PROCESSESSLOWLY VARYING FUNCTIONSPOINCARÉFUNCTIONAL EQUATION
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 4 , December 1977 , pp. 681 - 723
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer, Berlin.Google Scholar
[2] Cohn, H. (1977) Almost sure convergence of branching processes. Z. Wahrscheinlichkeitsth, 38, 73–81.Google Scholar
[3] Darling, D. A. (1970) The Galton–Watson process with infinite mean. J. Appl. Prob. 7, 455–456.Google Scholar
[4] Feller, W. (1970) An Introduction to Probability Theory and its Applications, Vol. 2. Wiley, New York.Google Scholar
[5] Foster, J. H. and Goettge, R. T. (1976) The rates of growth of the Galton-Watson process in varying environment. J. Appl. Prob. 13, 144–147.Google Scholar
[6] Grey, D. R. (1977) Almost sure convergence in Markov branching processes with infinite mean. J. Appl. Prob. 14, 702–716.CrossRefGoogle Scholar
[7] Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag, Berlin.Google Scholar
[8] Heyde, C. C. (1970) Extension of a result of Seneta for the supercritical Galton–Watson process. Ann. Math. Statist. 41, 739–742.CrossRefGoogle Scholar
[9] Hudson, I. L. and Seneta, E. (1977) The simple branching process with infinite mean. J. Appl. Prob. 14, 836–842.CrossRefGoogle Scholar
[10] Seneta, E. (1968) On recent theorems concerning the supercritical Galton–Watson process. Ann. Math. Statist. 39, 2098–2102.CrossRefGoogle Scholar
[11] Seneta, E. (1969) Functional equations and the Galton–Watson process. Adv. Appl. Prob. 1, 1–42.Google Scholar
[12] Seneta, E. (1973) The simple branching process with infinite mean I. J. Appl. Prob. 10, 206–212.CrossRefGoogle Scholar
[13] Seneta, E. (1974) Regularly varying functions in the theory of simple branching processes. Adv. Appl. Prob. 6, 408–420.Google Scholar
[14] Seneta, E. (1975) Normed-convergence theory for supercritical branching processes. Stoch. Proc. Appl. 3, 35–43.Google Scholar
[15] Seneta, E. (1976) Regularly varying functions. Lecture Notes in Mathematics 508, Springer-Verlag, Berlin.Google Scholar