No CrossRef data available.
Article contents
Correlations in bivariate point processes: some biological applications
Published online by Cambridge University Press: 01 July 2016
Extract
Let (Φ1 Φ2) be a bivariate point process. Let 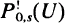 be the probability that (Φ1 Φ2) - (0, s) (the process without the 0 and s points) verify U when we have a point of <1>1 in the origin and a point of Φ2 in s. This is the reduced cross Palm distribution. Some correlation measures for bivariate point processes based on this reduced cross Palm distribution are proposed. Their estimators and expressions under the independence and the random labelling hypothesis are considered. The differences and improvements with respect to the cross intensity function and its integrated version, the cross
be the probability that (Φ1 Φ2) - (0, s) (the process without the 0 and s points) verify U when we have a point of <1>1 in the origin and a point of Φ2 in s. This is the reduced cross Palm distribution. Some correlation measures for bivariate point processes based on this reduced cross Palm distribution are proposed. Their estimators and expressions under the independence and the random labelling hypothesis are considered. The differences and improvements with respect to the cross intensity function and its integrated version, the cross  function (Stoyan et al. 1987), are studied. Some Monte Carlo tests for testing the independence and the random labelling hypothesis are proposed. They are applied to real bivariate point patterns: positions of hickories and maples in the Lansing Woods (Diggle 1983) and cases and controls of childhood leukaemia and lymphoma in North Humberside (Cuzick and Edwards 1990).
function (Stoyan et al. 1987), are studied. Some Monte Carlo tests for testing the independence and the random labelling hypothesis are proposed. They are applied to real bivariate point patterns: positions of hickories and maples in the Lansing Woods (Diggle 1983) and cases and controls of childhood leukaemia and lymphoma in North Humberside (Cuzick and Edwards 1990).
- Type
- Stochastic Geometry and Statistical Applications
- Information
- Copyright
- Copyright © Applied Probability Trust 1996


