Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T09:30:33.565Z Has data issue: false hasContentIssue false
  • English
  • Français

Comportement asymptotique des marches aleatoires associees aux polynomes de Gegenbauer et applications

Published online by Cambridge University Press:  01 July 2016

Leonard Gallardo
Leonard Gallardo*
Affiliation:
Université de Nancy II
*
∗Adresse postale: UER de Mathématiques et Informatique, Université de Nancy II, 23 Boulevard Albert 1er, 54000 Nancy, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

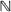Random walks on N associated with orthogonal polynomials have properties similar to classical random walks on . In fact such processes have independent increments with respect to a hypergroup structure on 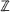with a convolution and a Fourier transform which is the basic tool for their study. We illustrate these ideas by giving a description of the asymptotic behaviour (CLT and ILL) of the random walks associated with Gegenbauer's polynomials. Moreover we can then use these random walks as a reference scale to deduce asymptotic properties of other Markov chains on 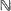via a comparison theorem which is of independent interest.

Keywords

GENERALIZED CONVOLUTIONSFOURIER-GEGENBAUER TRANSFORMSCENTRAL LIMIT THEOREM (NON-CLASSICAL)ITERATED LOG LAW (NON-CLASSICAL)COMPARISON OF TWO MARKOV CHAINS
Type
Research Article
Information
Advances in Applied Probability , Volume 16 , Issue 2 , June 1984 , pp. 293 - 323
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bibliographie

[1] Bloom, W. Et Heyer, H. (1982) The Fourier transform for probability measures on hypergroups. Rend. Mat. (VII)2, 315–334.Google Scholar
[2] Brezis, H., Rosenkrantz, W. Et Singer, B. (1971) An extension of Khintchine's estimate for large deviations to a class of Markov chains converging to a singular diffusion. Comm. Pure Appl. Math. 24, 705–726.Google Scholar
[3] ErdéLyi, A., (Ed.) (1953) Higher Transcendental Functions. Bateman Manuscript Project, Vol. 2. McGraw-Hill, New York.Google Scholar
[4] Eymard, P. Et Roynette, B. (1975) Marches aléatoires sur le dual de SU (2). Analyse harmonique sur les groupes de Lie, Lecture Notes in Mathematics 497, Springer-Verlag, Berlin, 108–152.Google Scholar
[5] Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
[6] George, C. (1975) Les chaînes de Markov associées à des polynômes orthogonaux. Thèse de doctorat, Nancy.Google Scholar
[7] Guivarc'H, Y., Kean, ?. Et Roynette, B. (1977) Marches aléatoires sur les groupes de Lie. Lecture Notes in Mathematics 624, Springer-Verlag, Berlin.Google Scholar
[8] Harris, T. E. (1952) First passage and recurrence distributions. Trans. Amer. Math. Soc. 73.Google Scholar
[9] Hylleras, E. (1962) Linearization of products of Jacobi polynomials. Math. Scand. 10, 189–200.Google Scholar
[10] Kingman, J. F. C. (1963) Random walks with spherical symmetry. Acta Math. 109, 11–53.Google Scholar
[11] Lamperti, J. (1962) A new class of probability limit theorems. J. Math. Mech. 11, 749–772.Google Scholar
[12] Lasser, R. (1983) Orthogonal polynomials and hypergroups. Rend. Mat. (to appear).Google Scholar
[13] Lord, R. D. (1954) the use of Hankel transform in statistics. Biometrika 41, 44–55.Google Scholar
[14] Neveu, J. (1972) Cours de probabilités. école Polytechnique, Paris.Google Scholar
[15] Rosenkrantz, W. (1966) A local limit theorem for a certain class of random walks. Ann. Math. Statist. 37, 288–290.Google Scholar
[16] Szegö, G. (1939) Orthogonal Polynomials. Amer. Math. Soc. Colloq. Publ. 23.Google Scholar