Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T18:01:04.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Absorption probabilities for Gaussian polytopes and regular spherical simplices

Part of: Geometric probability and stochastic geometry Stochastic processes General convexity Polytopes and polyhedra

Published online by Cambridge University Press:  15 July 2020

Zakhar Kabluchko  and
Dmitry Zaporozhets
Zakhar Kabluchko*
Affiliation:
Westfälische Wilhelms-Universität Münster
Dmitry Zaporozhets*
Affiliation:
St. Petersburg Department of Steklov Mathematical Institute
*
*Postal address: Orléans–Ring 10, 48149 Münster, Germany. Email: [email protected]
**Postal address: Fontanka 27, 191011 St. Petersburg, Russia.
Get access Rights & Permissions [Opens in a new window]

Abstract

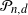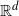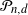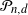The Gaussian polytope $\mathcal P_{n,d}$ is the convex hull of n independent standard normally distributed points in $\mathbb{R}^d$ . We derive explicit expressions for the probability that $\mathcal P_{n,d}$ contains a fixed point $x\in\mathbb{R}^d$ as a function of the Euclidean norm of x, and the probability that $\mathcal P_{n,d}$ contains the point 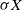$\sigma X$ , where 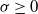$\sigma\geq 0$ is constant and X is a standard normal vector independent of $\mathcal P_{n,d}$ . As a by-product, we also compute the expected number of k-faces and the expected volume of $\mathcal P_{n,d}$ , thus recovering the results of Affentranger and Schneider (Discr. and Comput. Geometry, 1992) and Efron (Biometrika, 1965), respectively. All formulas are in terms of the volumes of regular spherical simplices, which, in turn, can be expressed through the standard normal distribution function 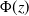$\Phi(z)$ and its complex version 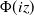$\Phi(iz)$ . The main tool used in the proofs is the conic version of the Crofton formula.

Keywords

Convex hullrandom polytopeGaussian polytopeGoodman–Pollack modelabsorption probabilityWendel’s formularegular simplexspherical geometrysolid angleconvex coneconic Crofton formulaaverage number of faceserror functionSchläfli’s function

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry 52A22: Random convex sets and integral geometry 52B11: $n$-dimensional polytopes
Secondary: 60G70: Extreme value theory; extremal processes 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces) 52A23: Asymptotic theory of convex bodies
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 2 , June 2020 , pp. 588 - 616
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (National Bureau of Standards Applied Mathematics Series 55). U.S. Government Printing Office, Washington.Google Scholar
Affentranger, F. (1991). The convex hull of random points with spherically symmetric distributions. Rend. Semin. Mat. Torino 49, 359–383.Google Scholar
Affentranger, F. and Schneider, R. (1992). Random projections of regular simplices. Discrete Comput. Geom. 7, 219–226.CrossRefGoogle Scholar
Amelunxen, D. and Lotz, M. (2017). Intrinsic volumes of polyhedral cones: a combinatorial perspective. Discrete Comput. Geom. 58, 371–409.CrossRefGoogle Scholar
Baryshnikov, Y. M. and Vitale, R. A. (1994). Regular simplices and Gaussian samples. Discrete Comput. Geom. 11, 141–147.CrossRefGoogle Scholar
Betke, U. and Henk, M. (1993). Intrinsic volumes and lattice points of crosspolytopes. Monatshefte Math. 115, 27–33.10.1007/BF01311208CrossRefGoogle Scholar
Bingham, N. H. and Doney, R. A. (1988). On higher-dimensional analogues of the arc-sine law. J. Appl. Prob. 25, 120–131.CrossRefGoogle Scholar
Böhm, J. and Hertel, E. (1981). Polyedergeometrie in n-dimensionalen Räumen konstanter Krümmung (Lehrbücher und Monographien aus dem Gebiete der Exakten Wissenschaften (LMW), Mathematische Reihe, 70). Birkhäuser, Basel, Boston.Google Scholar
Böröczky, K. and Henk, M. (1999). Random projections of regular polytopes. Arch. Math. 73, 465–473.CrossRefGoogle Scholar
Carnal, H. (1970). Die konvexe Hülle von n rotationssymmetrisch verteilten Punkten. Z. Wahrscheinlichkeitsth. 15, 168–176.10.1007/BF00531885CrossRefGoogle Scholar
Donoho, D. L. and Tanner, J. (2009). Counting faces of randomly projected polytopes when the projection radically lowers dimension. J. Amer. Math. Soc. 22, 1–53.10.1090/S0894-0347-08-00600-0CrossRefGoogle Scholar
Donoho, D. L. and Tanner, J. (2010). Counting the faces of randomly-projected hypercubes and orthants, with applications. Discrete Comput. Geom. 43, 522–541.10.1007/s00454-009-9221-zCrossRefGoogle Scholar
Efron, B. (1965). The convex hull of a random set of points. Biometrika 52, 331–343.10.1093/biomet/52.3-4.331CrossRefGoogle Scholar
Hadwiger, H. (1979). Gitterpunktanzahl im Simplex und Wills’sche Vermutung. Math. Ann. 239, 271–288.10.1007/BF01351491CrossRefGoogle Scholar
Hug, D. (2013). Random polytopes. In Stochastic Geometry, Spatial Statistics and Random Fields: Asymptotic Methods, Springer, Berlin, pp. 205–238.CrossRefGoogle Scholar
Hug, D., Munsonius, G. O. and Reitzner, M. (2004). Asymptotic mean values of Gaussian polytopes. Contributions to Algebra and Geometry 45, 531–548.Google Scholar
Jewell, N. P. and Romano, J. P. (1982). Coverage problems and random convex hulls. J. Appl. Prob. 19, 546–561.CrossRefGoogle Scholar
Jewell, N. P. and Romano, J. P. (1985). Evaluating inclusion functionals for random convex hulls. Z. Wahrscheinlichkeitsth. 68, 415–424.CrossRefGoogle Scholar
Kabluchko, Z. and Zaporozhets, D. (2019). Expected volumes of Gaussian polytopes, external angles, and multiple order statistics. Trans. Amer. Math. Soc. 372, 1709–1733.CrossRefGoogle Scholar
Majumdar, S. N., Comtet, A. and Randon-Furling, J. (2010). Random convex hulls and extreme value statistics. J. Statist. Phys. 138, 955–1009.10.1007/s10955-009-9905-zCrossRefGoogle Scholar
Raynaud, H. (1970). Sur l’enveloppe convexe des nuages de points aléatoires dans Rn. I. J. Appl. Prob. 7, 35–48.Google Scholar
Rényi, A. and Sulanke, R. (1963). Über die konvexe Hülle von n zufällig gewählten Punkten. Z. Wahrscheinlichkeitsth. 2, 75–84.10.1007/BF00535300CrossRefGoogle Scholar
Rogers, C. A. (1958). The packing of equal spheres. Proc. London Math. Soc. 8, 609–620.10.1112/plms/s3-8.4.609CrossRefGoogle Scholar
Ruben, H. (1954). On the moments of order statistics in samples from normal populations. Biometrika 41, 200–227.10.1093/biomet/41.1-2.200CrossRefGoogle Scholar
Ruben, H. (1960). On the geometrical moments of skew-regular simplices in hyperspherical space, with some applications in geometry and mathematical statistics. Acta Math. 103, 1–23.10.1007/BF02546523CrossRefGoogle Scholar
Schläfli, L. (1950). Theorie der vielfachen Kontinuität. In Gesammelte Mathematische Abhandlungen, Springer, pp. 167–387.CrossRefGoogle Scholar
Schneider, R. (2008). Recent results on random polytopes. Boll. Unione Mat. Ital. 1, 17–39.Google Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry (Probability and Its Applications). Springer, Berlin.CrossRefGoogle Scholar
Vershik, A. M. and Sporyshev, P. V. (1986). An asymptotic estimate for the average number of steps in the parametric simplex method. Zh. Vychisl. Mat. i Mat. Fiz. 26, 813–826, 958.Google Scholar
Vershik, A. M. and Sporyshev, P. V. (1992). Asymptotic behavior of the number of faces of random polyhedra and the neighborliness problem. Selecta Math. Soviet. 11, 181–201.Google Scholar
Wendel, J. G. (1962). A problem in geometric probability. Math. Scand. 11, 109–111.10.7146/math.scand.a-10655CrossRefGoogle Scholar