Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T03:08:24.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-Level Stabilized Finite Volume Methods for the Stationary Navier-Stokes Equations

Published online by Cambridge University Press:  03 June 2015

Tong Zhang  and
Shunwei Xu
Tong Zhang*
Affiliation:
School of Mathematics & Information Science, Henan Polytechnic University, Jiaozuo 454003, Henan, China
Shunwei Xu*
Affiliation:
School of Mathematics & Information Science, Henan Polytechnic University, Jiaozuo 454003, Henan, China
*
Corresponding author.Email: [email protected]
Email: [email protected]
Get access

Abstract

In this work, two-level stabilized finite volume formulations for the 2D steady Navier-Stokes equations are considered. These methods are based on the local Gauss integration technique and the lowest equal-order finite element pair. Moreover, the two-level stabilized finite volume methods involve solving one small Navier-Stokes problem on a coarse mesh with mesh size H, a large general Stokes problem for the Simple and Oseen two-level stabilized finite volume methods on the fine mesh with mesh size 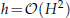or a large general Stokes equations for the Newton two-level stabilized finite volume method on a fine mesh with mesh size 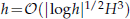. These methods we studied provide an approximate solution 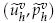with the convergence rate of same order as the standard stabilized finite volume method, which involve solving one large nonlinear problem on a fine mesh with mesh size h. Hence, our methods can save a large amount of computational time.

Keywords

65N3065N0876D05Stationary Navier-Stokes equationsfinite volume methodtwo-level methoderror estimate
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 5 , Issue 1 , February 2013 , pp. 19 - 35
Copyright
Copyright © Global-Science Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bank, R. and Rose, D., Some error estimates for the box method, SIAM J. Numer. Anal., 24 (1987), pp. 777–787.Google Scholar
[2]Bi, C. J. and Ginting, V., Two-grid finite volume element method for linear and nonlinear elliptic problems, Numer. Math., 108 (2007), pp. 177–198.Google Scholar
[3]Bochev, P., Dohrmann, C. and Gunzburger, M., Stabilization of low-order mixed finite elements for the Stokes equations, SIAM J. Numer. Anal., 44 (2006), pp. 82–101.CrossRefGoogle Scholar
[4]Breezzi, F. and Pitkäranta, J., On the stabilisation of finite element approximations of the Stokes problems, in: Hackbusch, W. (Ed.), Efficient Solutions of Elliptic Systems, Notes on Numerical Fluid Mechanics, Vol. 10, Vieweg, Braunschweig, 1984.Google Scholar
[5]Brenner, S. and Scott, L., The Mathematical Theory of Finite Element Methods, Spring-Verlag, 1994.CrossRefGoogle Scholar
[6]Brooks, A. and Hughes, T., Streamline upwind/ Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations, Comput. Methods Appl. Mech. Eng., 32 (1982), pp. 199–259.CrossRefGoogle Scholar
[7]Chen, Z. X., Finite Element Methods and Their Application, Spring-Verlag, Heidelberg, 2005.Google Scholar
[8]Ciarlet, P., The Finite Element Method for Elliptic Problems, Amsterdam: North-Holland, 1978.Google Scholar
[9]Dawson, C. and Wheeler, M., Two-grid methods for mixed finite element approximations of nonlinear parabolic equations, Contemp. Math., 180 (1994), pp. 191–203.Google Scholar
[10]Dawson, C., Wheeler, M. and Woodward, C., A two-grid finite difference scheme for nonlinear parabolic equations, SIAM J. Numer. Anal., 35 (1998), pp. 435–452.Google Scholar
[11]Dohrmann, C. and Bochev, P., A stabilized finite element method for the Stokes problem based on polynomial pressure projections, Int. J. Numer. Methods Fluids, 46 (2004), pp. 183–201.Google Scholar
[12]Douglas, J. and Wang, J. P., A absolutely stabilized finite element method for the Stokes problem, Math. Comput., 52 (1989), pp. 495–508.Google Scholar
[13]Ewing, R., Lin, T. and Lin, Y. P., On the accuracy of the finite volume element based on piecewise linear polynomials, SIAM J. Numer. Anal., 39 (2002), pp. 1865–1888.Google Scholar
[14]Eymard, R., Gallouet, T. and Herbin, R., Finite volume methods, Handbook Numer. Anal., Ciarlet, P.G. and Lions, J.L. eds, (1997), pp. 713–1020.Google Scholar
[15]Girault, V. and Raviart, P. A., Finite Element Method for Navier-Stokes Equations: Theory and Algorithms, Springer-Verlag, Berlin, Herdelberg, 1987.Google Scholar
[16]He, Y. N., Two-level method based on finite element and Crank-Nicolson extrapolation for the time-dependent Navier-Stokes equations, SIAM J. Numer. Anal., 41 (2003), pp. 1263–1285.Google Scholar
[17]He, Y. N. and Li, J., A stabilized finite element method based on local polynomial pressure projection for the stationary Navier-Stokes equations, Appl. Numer. Math., 58 (2008), pp. 1503–1514.Google Scholar
[18]He, Y. N. and Li, K. T., Two-level stabilized finite element methods for steady Navier-Stokes equations, Computing, 75 (2005), pp. 337–351.Google Scholar
[19]Heywood, J. and Rannacher, R., Finite element approximation of the nonstationary Navier-Stokes problem I; regularity of solutions and second-order error estimates for spatial discretization, SIAM J. Numer. Anal., 19 (1982), pp. 275–311.Google Scholar
[20]Layton, W. and Leferink, J., Two-level Picard and modified Picard methods for the Navier-Stokes equations, Appl. Math. Comput., 69 (1995), pp. 263–274.Google Scholar
[21]Li, R. H. and Zhu, P. Q., Generalized difference methods for second order elliptic paratial differential equations (I)-triangle grids, Numer. Math. J. Chinese Universities, 2 (1982), pp. 140–152.Google Scholar
[22]Li, J. and Chen, Z. X., A new stabilized finite volume method for the stationary Stokes equations, Adv. Comput. Math., 30 (2009), pp. 141–152.Google Scholar
[23]Li, J., He, Y. N. and Chen, Z. X., A new stabilized finite element method for the transient Navier-Stokes equations, Comput. Methods Appl. Mech. Eng., 197 (2007), pp. 22–35.Google Scholar
[24]Li, J., Mei, L. Q. and He, Y. N., A pressure-Poisson stabilized finite element method for the non-stationary Stokes equations to circumvent the inf-sup condition, Appl. Math. Comput., 182 (2006), pp. 24–35.Google Scholar
[25]Li, J., Shen, L. H. and Chen, Z. X., Convergence and stability of a stabilized finite volume method for the stationary Navier-Stokes equations, BIT Numer. Math., 50 (2010), pp. 823–842.Google Scholar
[26]Temam, R., Navier-Stokes Equation: Theory and Numerical Analysis (Third edition), North-Holland, Amsterdam, New York, Oxford, 1984.Google Scholar
[27]Wu, H. J. and Li, R. H., Error estimates for finite volume element methods for general second-order elliptic problems, Numer. Methods Partial Differential Eq., 19 (2003), pp. 693–708.Google Scholar
[28]Xu, J. C., A novel two-grid method for semi-linear elliptic equations, SIAM J. Sci. Comput., 15 (1994), pp. 231–237.Google Scholar
[29]Xu, J. C., Two-grid discretization techniques for linear and nonlinear PDEs, SIAM J. Numer. Anal., 33 (1996), pp. 1759–1777.CrossRefGoogle Scholar
[30]Ye, X., On the relationship between finite volume and finite element methods applied to the Stokes equations, Numer. Methods Partial Differential Eq., 17 (2001), pp. 440–453.Google Scholar
[31]Zhang, T., The semidiscrete finite volume element method for nonlinear convection-diffusion problem, Appl. Math. Comput., 217 (2011), pp. 7546–7556.Google Scholar
[32]Zhang, T. and He, Y. N., Fully discrete finite element method based on pressure stabilization for the transient Stokes equations, Math. Comput. Simulat., 82 (2012), pp. 1496–1515.CrossRefGoogle Scholar
[33]Zhang, T., Si, Z. Y. and He, Y. N., A stabilised characteristic finite element method for transient Navier-Stokes equations, Int. J. Comput Fluid D., 24 (2010), pp. 369–381.CrossRefGoogle Scholar